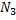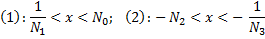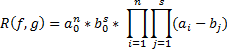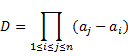Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы линейной алгебры и многомерной геометрииСодержание книги
Поиск на нашем сайте
Глава 4 Элементы линейной алгебры и многомерной геометрии Параграф 2. Подпространства Пусть дано ЛВП V Непустое множество v’ называется подпространством ЛВП V если выполнены условия: 1) Сумма любых двух векторов из множества v’ также является вектором этого множества
2) Произведение любого вектора V’ на скаляр(число) так же является вектором данного множества V’
Ядро гомоморфизма Пусть дан гомоморфизм Ядром гомоморфизма f называется множество всех таких векторов из ЛВП V, образом которых является нулевой вектор ЛВП W.
Образ гомоморфизма Образом гомоморфизма f называется множество все нетривиальных векторов ЛВП W являющихся образами ненулевых векторов из ЛВП V:
Теорема о ядре и образе гомоморфизма: Пусть Ядро гомоморфизма f является подпространством ЛВП V
Образ гомоморфизма f является подпространством ЛВП W.
Доказательство: 1) Покажем что ядро гомоморфизма f является подпространство ЛВП V. - Выберем 2 элемента - Проверим выполняются ли понятие подпространства и основные свойства понятия гомоморфизма:
Из равенства (1) видно, что сумма двух векторов из ядра имеет образ нуль –вектора ЛВП W. Это означает что сумма двух векторов принадлежит ядру гомоморфизма (Первое условие определения подпространства.)
Из неравенства (2) следует, что произведение произвольного скаляра на произвольный вектор x из ядра, так же является вектором из ядра (второе условие определения подпространства) 2) Покажем, что образ гомоморфизма f является подпространством ЛВП W - Выберем x’ и y’ из образа f - Проверим выполняется ли понятие подпространства и основные свойства понятия гомоморфизма.
Так как сумма векторов x’ и y’ не является нуль-вектором Доказательство второго свойства гомоморфизма основываются на приведенных выше выкладках. Теорема о простейших свойствах гомоморфизмов: Пусть 1) 2) Теорема о простейших свойствах изомофризма: Пусть 1) Образом любого ненулевого вектора из V является ненулевой вектор из W
2) 3) Образами векторов, образующих линейно независимую систему в ЛВП V, являются векторами их ЛВП W, которые так же образуют линейно независимую систему.
4) Пусть дана произвольная линейно зависимая система векторов из ЛВП V, причем их линейная комбинация (не тривиальная), приравнена к Пересечение и сумма подпространств ЛВП. Пусть даны подпространства v’’ и v’. Пересечение подпространств v’ и v’’ называется множество векторов принадлежащих одновременно и v’ и v’’
Теорема о пересечении подпространств: Пересечение любых двух подпространств ЛВП является подпространством исходного ЛВП. Доказательство: Самостоятельно детишки) Примечание к теореме: Не всегда имеет место тот факт, что объединение двух подпространств ЛВП являются подпространством исходного ЛВП. Суммой двух подпространств v’ и v’’ называется множество всевозможных линейных комбинаций из двух векторов принадлежащих соответственно v’ и v’’
Теорема о сумме подпространств: Сумма любых двух подпространств ЛВП является подпространством исходного ЛВП. Доказательство: И тут снова самостоятельно) Размерностью Подпространства, как и самого пространства называется число базисных векторов соответственно. Обозначение: dimV Теорема о размерности ЛВП:
Размерность пространства равна сумме размерностей заданных подпространств за исключением размерностей пересечений подпространств, составляющих собой исходное ЛВП. Прямой суммой двух подпространств v’ и v’’ называется обычная сумма при условии что эти подпространства не пересекаются
Теорема о прямой сумме: Размерность ЛВП равна сумме размерностей непересекающихся подпространств
Теорема о размерности ядра и образа гомоморфизма:
Если dimV=n; dim(kerf)=r, То dim(Imf)=n-r Доказательство: Пусть размерность V (dimV) равна n и И Предположим что векторы Получим: Предположим противное, то есть
Далее, пользуясь понятием гомоморфизма, получаем следующее:
НО! Полученный результат противоречит тому факту, что векторы Покажем, что это действительно так. Воспользуемся свойствами гомоморфизма и понятием ядра
Из вышеприведенных рассуждений видно, что произвольный ненулевой вектор y из ЛВП W(представим) разложим по базису Линейное многообразие Пусть дано n- мерное ЛВП
И ей дана присоединенная (соответствующая) система линейных уравнений(**) Будем считать, что каждая система (*) и (**) имеет ранг основной матрицы, равный r и введем обозначение s=n-r. Совокупность всех решений системы (*) (точек ЛВП Согласно теореме о решениях системы СЛНУ и присоединенной системы СЛОУ можно сказать что линейное многообразие представляет собой множество \совокупность всех решений системы (**), к каждому из которых прибавлено некоторое частное решение системы (*)
Таким образом второе определение линейного многообразия имеет вид:
Можно считать, что совокупность решений (**) представляет собой некоторую плоскость в n- мерном пространстве Пусть ко всем векторам этой плоскости прибавлен некоторый произвольный вектор а из пространства Плоскость П будет собой представлять плоскость П(0) сдвинутую на вектор а. Концы всех векторов полученных путем сложения векторов плоскости П(0) и фиксированного вектора а, представляет собой плоскость П, и каждый из них согласно вышеуказанной теореме о связи решений, совокупность всех решений системы (*). Верно и обратное: Пусть дана система (**) (Плоскость П(0)), и некоторый произвольный вектор А из пространства
В силу произвольности выбора вектора А, легко понять, что вектор А не единственный и система (***) представляет собой систему (*). Таким образом, множество всех решений системы (*) (плоскость П) представляет собой множество всех решений системы (**) (Плоскость П(0)), к каждому из которых прибавлен произвольный фиксированный вектор А, имеющий собой некоторое частное решение системы (*). Линейное многообразие (*) называется s-мерным если пространство порожденное системой так же является s- мерным. S- мерыне плоскости в аффинном пространстве. Пусть дано аффинное пространство Вновь рассмотрим систему (*) и на этой основе «родим» следующее определение: Множество\совокупность всех точек из аффинного пространства Одномерные плоскостью. Называются прямыми. Плоскости размерность которых больше 1 и меньше n называются гиперплоскостями. Всякую гиперплоскость можно задать системой линейных неоднородных уравнений вида (*). Например гиперплоскость размерности n-1 можно задать с помощью одного уравнения (s=n-r=n-n+1=1):
Легко показать, что при переходе от одного начала координат к другому в аффинном пространстве Пусть П – некоторая s- мерная плоскость, удовлетворяющая системе (*). П(0) – такая же s- мерная плоскость, проходящая через начало координат. Если ко всеем векторам П(0) прибавить произвольный вектор А из Две S- мерные гиперплоскости параллельны, если определяющие их системы вида (*) таковы, что присоединенные системы являются равносильными. То есть имеют одни и те же решения. Две s- мерные гиперплоскости называются пересекающимися, если определяющие их системы вида (*) таковы, что присоединенные системы имеют общее решение, которое составлено из уравнений присоединенных систем. S- мерная плоскость = П(0) и N – Мерная гиперплоскость = П(1) называются параллельными, если гиперплоскость П(0) параллельная любой гиперплоскости содержащейся в гиперплоскости П(1). Другими словами, всякое решение присоединенной системы характеризующей гиперплоскость П(1), является решением присоединенной системы, характеризующей гиперплоскость П(0). То есть, иначе говоря, СЛОУ, характеризующая гиперплоскость П(1), является следствием СЛОУ, характеризующей П(0) Пусть П – s- мерная гиперплоскость. Общее решение присоединенной системы, характеризующей гиперплоскость п(системы (*)и (**)), имеет вид
Или
Переходя к координатной записи, получаем параметрическое задание плоскости П:
Примечание: 1) Если гиперплоскость П оказалась прямой, то фундаментальное решение системы (**) будет единственным, и вследствие этого константа а будет иметь единственное значение. Исключая параметр «а» из системы (****) получаем каноническое уравнение прямой. (учим геометрию господа) 2) Если гиперплоскость П оказалась двухмерной плоскостью, то (система (****)) будет иметь два фундаментальных решения системы (**). Следовательно, будет 2 параметра: «а1» и «а2». Тогда система (****) будет иметь вид:
S- мерная плоскость = П(0) и N – Мерная гиперплоскость = П(1) называются пересекающимися если, СЛНУ (*), составленная из СЛНУ, задающих эти гиперплоскости, имеет решение.
Глава 6. Кольцо полиномов К Параграф 1 Общее сведения. Полиномом n-ой степени с коэффициентами из числового множества R одной неизвестной называется выражение вида
Где X – переменная, объект не принадлежащий числовому множеству R. N=degF – (Степень многочлена F) (Целое положительное число) В силу своего конструктивного построения полиномом является символьной записью, поэтому для такой формы задания вводится понятие равенство многочлена. Два многочлена называются равными, если коэффициенты при соответствующих степенях являются равными. Впоследствии выяснилось, что многочлен можно воспринимать как функцию от одного или нескольких неизвестных. В силу этого, равенство многочленов можно рассматривать как равенство функций, то есть при одинаковых значения аргумента они принимают равные значения функции. Множество полиномов образует кольцо, но не поле. В поле для любого ненулевого элемента можно найти ему обратный. Во множестве полиномов это невозможно.
Многочлены полиномы нулевой степени можно отождествлять с числами из некоторого числового множества, над которыми строится многочлен (полином) Некоторыми особыми характеристиками обладает нулевой полином. То есть степень данного полинома считается неопределенной (равна бесконечности) В силу своих свойств нулевых многочленов бесконечное множество и принято считать что они эквивалентны друг другу. Операции над полиномами (основные): 1) Сложении полиномов
Суммой двух полиномов f и g называется полином (f+g), коэффициенты которого определяются по правилу 2) Умножение полиномов: Произведением двух полиномов f и g называется полином (f*g) коэффициенты которого определяются по правилу: И понятно, что Произведение двух ненулевых многочленов никогда не является нулевым многочленом. 3) В кольце полиномов операция деления не определена, но множество полиномов обладает свойствами числовых множеств. В следствии этого можно ввести аналог деления, который называется «Алгоритм Евклида» Теорема (о делении с остатком): Пусть даны f и g. degF=n и degG=m, причем полиномы не нулевые и n больше m. Тогда существуют такие многочлены q И r, являющиеся единственными, и для которых выполнимо равенство
q- это частное от деления, а r - остаток. Доказательство: 1) Покажем единственность q и r
Рассмотрим равенство (*). Степень разности r1-r2 меньше степени многочлена g. (согласно условию теоремы) А степень произведения g на (q1-q2) являются большей или равной степени многочлена q. При предположении, что q1 В силу этого заключаем, что степень q1-q2 должна быть равна степени нулевого, то есть q1=q2 и r1=r2 (второе слагаемое должно быть нулевым многочленом) 2) Конструктивное построение деления полиномов.
Домножая многочлен меньшей степени на соответствующее выражение таким образом, что бы после вычитания из многочлена старшей степени коэффициенты при старших степенях становились равными нулю.
До тех пор, пока степень многочлена, получающегося после вычитания, не окажется строго меньше степени g. В итоге получим, что степень оставшегося многочлена удовлетворяет условиям теоремы и является степенью остатка (degn).
Доказательство: Самостоятельно. Параграф 4. Границы корней Лемма(о модуле старшего члена):
Для любого полинома f с коэффициентами из поля C, причем degF>0, при стремлении переменной x к бесконечности найдется такое k(>0), что имеет место:
Рассмотрим серию верхних оценок положительных корней: 1) 2) Максимум при корне означает выбор максимального значения среди коэффициентов за исключением а(n) и a(n-1) 3) Где s – подходящая степень корня для требуемой точности оценки. А(к) – произвольный коэффициент, исключая а(n) Данные оценки можно использовать для нахождения верхней границы корней полинома. Для нахождении интервала (и для отрицательных корней) можно пользоваться вышеуказанной оценкой и системой оценок полученных из следующих вычислений:
Предложение о границах корней полинома: Положительные корни многочлена f будут оцениваться интервалом (1), а отрицательные интервалом (2)
N(0) верхняя граница корней полинома f. Примечание: Для оценки границ корней многочлена можно использовать одновременно несколько разных оценок. Результат и дискриминант. Пусть дан многочлен f с коэффициентами из поля р. Если многочлен зависит от нескольких переменных, то такой набор чисел из р, при котором после подстановки их вместо переменных в многочлен f он принимает значение нуля, называется решение многочлена f. Всякий многочлен имеет решение. Два многочлена называются взаимно простыми если они не имеют общих решений (или корней) Два многочлена обладают общим корнем тогда и только тогда, когда они не являются взаимно простыми над некоторым полем Р. Для решения вопроса о наличии общих корней для двух многочленов вводится понятие результата, который определяется следующим образом.
Теорема о результате: Два многочлена f(x) и g(x) имеют общий корень тогда и только тогда, когда из результат равен нулю. Результат двух многочленов может быть представлен в виде полинома выраженного через коэффициенты многочленов f И g или в виде детеминанта порядка n+s. Он дохуя большой и я его не могу писать. Пусть дан многочлен Пусть а1,а2,..,аn. – корни многочлена f(x). Возникает вопрос, будут ли среди данных чисел равные между собой. Они будут, если величина называемая дискриминантом f(x) будет равна нулю.
Многочлен f будет обладать кратными корнями тогда и только тогда, когда его дискриминант равен нулю, а так же в случае когда многочлен f и его первая производная обладает общими корнями. Глава 4 Элементы линейной алгебры и многомерной геометрии
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.239.65 (0.01 с.) |

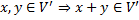

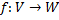
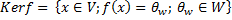
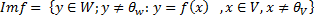


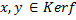
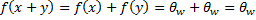 (1)
(1)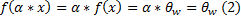
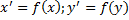
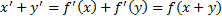
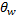 и согласно определению ядра, эта сумма является образом сумы двух ненулевых векторов из ЛВП V.
и согласно определению ядра, эта сумма является образом сумы двух ненулевых векторов из ЛВП V.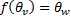

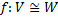 . Имеют место следующие простейшие свойства:
. Имеют место следующие простейшие свойства:
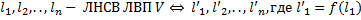 , такие ЛНВС ЛВП W/
, такие ЛНВС ЛВП W/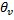 , с некоторыми скалярами
, с некоторыми скалярами  тогда образом этой системы будет являтся так же линейно зависимая система векторов. При чем нетривиальная линейная комбинация образов приравненная к
тогда образом этой системы будет являтся так же линейно зависимая система векторов. При чем нетривиальная линейная комбинация образов приравненная к 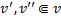

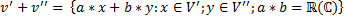
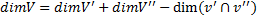
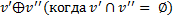
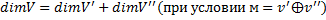

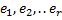 – это базис гомоморфизма (kerf)
– это базис гомоморфизма (kerf)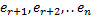 – дополнение до базиса пространства V.
– дополнение до базиса пространства V.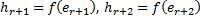 ,..,
,.., 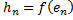
 образуют линейно зависимую систему. Согласно понятию линейной зависимости существует нетривиальная линейная комбинация такая, что
образуют линейно зависимую систему. Согласно понятию линейной зависимости существует нетривиальная линейная комбинация такая, что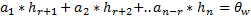
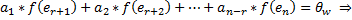
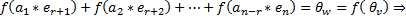
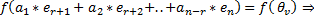
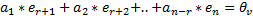
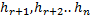 образуют линейно независимую систему (исключаем второе предположение), то есть эта система является кандидатом на роль базиса в ЛВП W.
образуют линейно независимую систему (исключаем второе предположение), то есть эта система является кандидатом на роль базиса в ЛВП W.
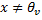
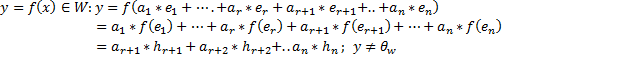
 , над множеством R(или С), и дана система линейных неоднородных уравнений (*)
, над множеством R(или С), и дана система линейных неоднородных уравнений (*)
 – алгебраический вектор, равный суме всех фундаментальных решений системы (*) с некоторыми скалярами; частное решение систем (*) обозначим через а, и обозначим через х общее решение системы (*)
– алгебраический вектор, равный суме всех фундаментальных решений системы (*) с некоторыми скалярами; частное решение систем (*) обозначим через а, и обозначим через х общее решение системы (*)

 размерности n в котором выбрано некоторое начало координат.
размерности n в котором выбрано некоторое начало координат.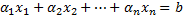
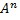 ранг системы (*) не уменьшается.
ранг системы (*) не уменьшается.
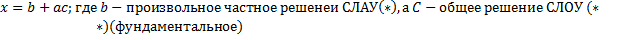
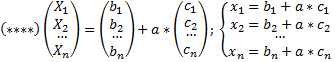


 старший коэффициент, а
старший коэффициент, а 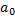 младший, свободный коэффициент
младший, свободный коэффициент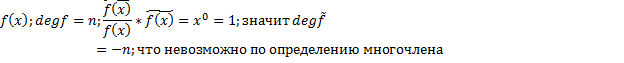
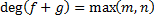
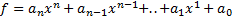
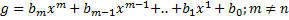
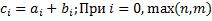

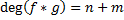
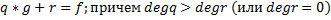

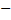
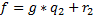
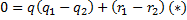
 q2. Что невозможно.
q2. Что невозможно.
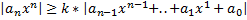
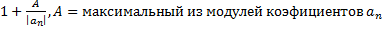
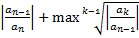

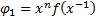 – для него можно найти верхнюю границу корней
– для него можно найти верхнюю границу корней 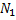
 и для него найдем верхнию границу корней
и для него найдем верхнию границу корней 
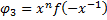 верхняя граница корней которого равна
верхняя граница корней которого равна