
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Поле комплексных чисел сСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Непустое множество К с бинарными операциями сложения и умножения называется полем(числовым полем), если выполнены следующие аксиомы: 0) Бинарные операции сложения и умножения являются замкнутыми. 1) Бинарные операции сложения и умножения являются коммутативными A+b=b+a и a*b=b*a 2) Бинарные операции являются ассоциативными:
3) Имеет место закон дистрибутивности умножения относительно сложения.
4) Каждый ненулевой элемент имеет себе обратный, и каждый элемент имеет себе противоположный. 5) Общая группа аксиом связанных с другими свойствами элементов. Рассмотрим поле действительных чисел R и на его основе рассмотрим множество всевозможных, упорядоченных пар вида (а,0) для которых выполняются законы: 1) 2) 3) Роль единичного элемента играет пара вида Получается множество, состоящее из объектов отличных от действительных чисел, для которых выполнены все законы действительных чисел (включая законы 1-3 выше) Таким образом поле действительных чисел R и новое множество являются изоморфными. Теперь рассмотри множество всех упорядоченных пар вида Возникает вопрос, будет ли данное множество изоморфно множеству чисел R. Такое множество найти МОЖНО!!!!!!(Он сам велел дофига знаков поставить) Нужно лишь для пар 1) 2) 3) 4) Роль единичного элемента играет пара вида 5) Особую роль единичного элемента играет пара вида (0;1) Перемножим Элемент То есть квадрат элемента (0;1) равен отрицательному числу..(!!!!!!) Поэтому пара (0;1) обозначается I и называется «мнимой единицей» для которой имеет место
Множество всех упорядоченных пар Алгебраическая форма комплексного числа
Модули комплексного числа z называется величина
Комплексное число Теорема об отношениях сравнения на поле комплексных чисел С: Поле комплексных чисел не является упорядоченным, то есть сравнивать 2 комплексных числа с помощью бинарного отношения типа сравнения (<,<=) невозможно. Два комплексных числа называются равными, когда выполнено условие:
Простейшие свойства комплексных чисел: 1) 2) 3) 4) Теорема об алгебраических операция над комплексными числами: Пусть дано: 1) 2) 3) 4) 5) 6)
Параграф 2. Комплексные числа в тригонометрической форме Пусть дано число (Тут какой то рисунок в лекции..я перерисовывать его не буду)
(Ребят, в ворде «альфа» не отличается почти от «а». не перепутайте! В аргументе у косинуса и синуса стоит «Альфа», а в самих формулах «а») Угол наклона комплексного числа к оси действительных частей называется аргументом комплексного числа.
(Тут опять же «альфа») Теорема (об операциях над комплексными числами в тригонометрической форме): Пусть даны:
1) 2) 3) При делении комплексных чисел аргументы вычитаются, а при умножении складываются. 4) 5) Возведение комплексного числа в степень (формула Муавра)
6) Общая формула Муавра
Комплексные числа в форме Эйлера.
Операции над комплексными числами в форме Эйлера: 1) 2) 3) 4) 5) 6)
Группа корней n-ой степени из единицы:
Комплексные числа При сложении и умножении чисел
Глава 6. Кольцо полиномов К Параграф 1 Общее сведения. Полиномом n-ой степени с коэффициентами из числового множества R одной неизвестной называется выражение вида
Где X – переменная, объект не принадлежащий числовому множеству R. N=degF – (Степень многочлена F) (Целое положительное число) В силу своего конструктивного построения полиномом является символьной записью, поэтому для такой формы задания вводится понятие равенство многочлена. Два многочлена называются равными, если коэффициенты при соответствующих степенях являются равными. Впоследствии выяснилось, что многочлен можно воспринимать как функцию от одного или нескольких неизвестных. В силу этого, равенство многочленов можно рассматривать как равенство функций, то есть при одинаковых значения аргумента они принимают равные значения функции.
Множество полиномов образует кольцо, но не поле. В поле для любого ненулевого элемента можно найти ему обратный. Во множестве полиномов это невозможно.
Многочлены полиномы нулевой степени можно отождествлять с числами из некоторого числового множества, над которыми строится многочлен (полином) Некоторыми особыми характеристиками обладает нулевой полином. То есть степень данного полинома считается неопределенной (равна бесконечности) В силу своих свойств нулевых многочленов бесконечное множество и принято считать что они эквивалентны друг другу. Операции над полиномами (основные): 1) Сложении полиномов
Суммой двух полиномов f и g называется полином (f+g), коэффициенты которого определяются по правилу 2) Умножение полиномов: Произведением двух полиномов f и g называется полином (f*g) коэффициенты которого определяются по правилу: И понятно, что Произведение двух ненулевых многочленов никогда не является нулевым многочленом. 3) В кольце полиномов операция деления не определена, но множество полиномов обладает свойствами числовых множеств. В следствии этого можно ввести аналог деления, который называется «Алгоритм Евклида» Теорема (о делении с остатком): Пусть даны f и g. degF=n и degG=m, причем полиномы не нулевые и n больше m. Тогда существуют такие многочлены q И r, являющиеся единственными, и для которых выполнимо равенство
q- это частное от деления, а r - остаток. Доказательство: 1) Покажем единственность q и r
Рассмотрим равенство (*). Степень разности r1-r2 меньше степени многочлена g. (согласно условию теоремы) А степень произведения g на (q1-q2) являются большей или равной степени многочлена q. При предположении, что q1 В силу этого заключаем, что степень q1-q2 должна быть равна степени нулевого, то есть q1=q2 и r1=r2 (второе слагаемое должно быть нулевым многочленом) 2) Конструктивное построение деления полиномов.
Домножая многочлен меньшей степени на соответствующее выражение таким образом, что бы после вычитания из многочлена старшей степени коэффициенты при старших степенях становились равными нулю.
До тех пор, пока степень многочлена, получающегося после вычитания, не окажется строго меньше степени g. В итоге получим, что степень оставшегося многочлена удовлетворяет условиям теоремы и является степенью остатка (degn).
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.116.239 (0.012 с.) |

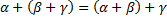
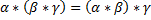

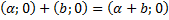
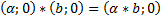
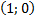 , а нулевого
, а нулевого 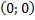
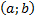
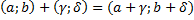
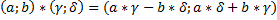
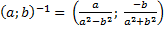
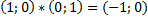
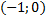 изоморфен -1(числу).
изоморфен -1(числу).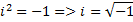
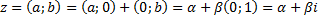
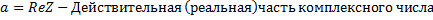
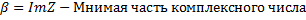
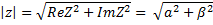
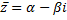 называется комплексно сопряженным числу z
называется комплексно сопряженным числу z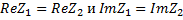
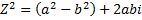
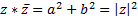
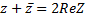
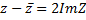
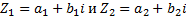
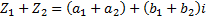

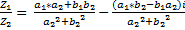
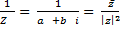
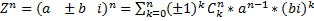 (Короче обычное раскрытие скобок, по биному ньютона)
(Короче обычное раскрытие скобок, по биному ньютона)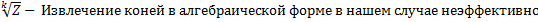
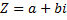
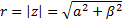
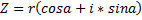
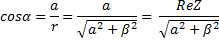
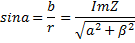
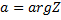
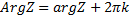
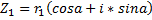
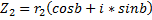
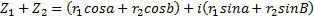
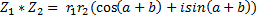
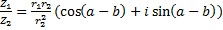
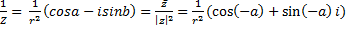
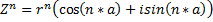
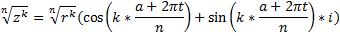
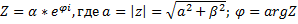
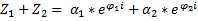
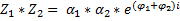
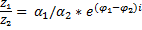
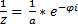
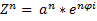
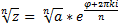
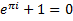
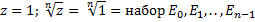
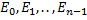 разбивают единичную окружность на равные части. Получаем правильный многоугольник.
разбивают единичную окружность на равные части. Получаем правильный многоугольник.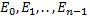 всегда получаются числа из этой же группы. Любое комплексное число можно выразить через
всегда получаются числа из этой же группы. Любое комплексное число можно выразить через 
 старший коэффициент, а
старший коэффициент, а 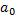 младший, свободный коэффициент
младший, свободный коэффициент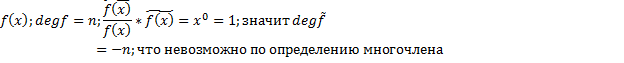
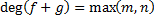
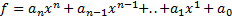
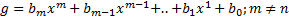
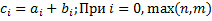

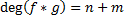
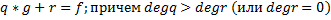

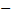
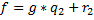
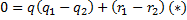
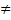 q2. Что невозможно.
q2. Что невозможно.



