
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа с комплексными числамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В математических операциях с комплексными числами используются функции из раздела «инженерные». Если функции недоступны, следует установить дополнение Пакет Анализа, а затем включить его с помощью диспетчера надстроек. Все функции работы с комплексными числами (табл. 3.14) допускают обозначение для мнимой единицы " i " или " j ", но не "I" или "J". Использование верхнего регистра приводит к получению ошибки (#ЗНАЧ!). Функции, которые используют не меньше двух комплексных чисел, требуют, чтобы обозначение мнимой единицы было одно и то же. Таблица 3.14
Почти все функции из рассматриваемого класса работают с текстовым параметром «комплексное число». Если параметр не представлен в форме x + yi или x + yj, то функция возвращает значение ошибки #ЧИСЛО! Пояснения и примеры КОМПЛЕКСН(3;4) равняется 3 + 4 i;КОМПЛЕКСН(3;4;"j") равняется 3 + 4 j; КОМПЛЕКСН(0;1) равняется i; КОМПЛЕКСН(1;0) равняется 1; МНИМ.ВЕЩ("6-9i") равняется 6 МНИМ.ЧАСТЬ("3+4i") равняется 4; МНИМ.ЧАСТЬ("0-j") равняется -1; МНИМ.ЧАСТЬ(4) равняется 0. МНИМ.СОПРЯЖ("3+4i") равняется 3 - 4i МНИМ.РАЗН("13+4i";"5+3i") равняется 8 + i МНИМ.СУММ("3+4i";"5-3i") равняется 8 + i Функция МНИМ.ABS(КЧ) возвращает абсолютную величину Функция МНИМ.АРГУМЕНТ(КЧ) возвращает значение аргумента комплексного числа, т.е. угол Пример: МНИМ.АРГУМЕНТ("3+4i") равняется 0,927295. Функция МНИМ.ПРОИЗВЕД(КЧ 1; КЧ 2;...) возвращает произведение от 2 до 29 комплексных чисел. Пример: МНИМ.ПРОИЗВЕД("3+4i";"5-3i") равняется 27 + 11i. Функция МНИМ.ДЕЛ(КЧ 1; КЧ 2) возвращает частное от деления двух комплексных чисел. Пример: МНИМ.ДЕЛ("-238+240i";"10+24i") равняется 5 + 12i. Самостоятельная работа
· · Составить и отладить таблицу расчета напряжения в конце ЛЭП в комплексных величинах по образцу рис. 3.13. Прогнозирование нагрузок Одной из достаточно сложных задач развития ЭЭС является прогнозирование нагрузок и электропотребления. Здесь сильно сказывается вероятностный характер и неопределенность исходных данных, поэтому существует определенный скепсис к формализованным методам прогнозирования. Однако эти методы позволяют осуществить обработку больших объемов информации и выявить существующие тенденции прогнозируемых показателей. Как правило, процедура прогнозирования подразделяется на два этапа: - предварительный анализ и интерполяция статистических временных зависимостей; - экстраполяция и коррекция выбранной математической функции прогноза. Предварительный анализ временной зависимости На этапе предварительного анализа определяется общий вид моделирующих функций, или, как их называют, функций-предикторов, и определяется масштаб моделирования значений временного ряда (иногда желателен переход к логарифмическому масштабу). Выбор математической модели зависит от сроков упреждения прогнозов: долгосрочные (свыше 10 лет); среднесрочные (5-10 лет); краткосрочные (1-3года); оперативные (от нескольких часов до года). При решении задач перспективного развития ЭЭС (свыше 5 лет) представляет интерес характер изменения годовых максимумов нагрузки энергосистемы. При планировании капитальных ремонтов основного оборудования ЭЭС - месячных максимумов, при планировании текущих ремонтов - суточных максимумов, при распределении нагрузки энергосистемы между параллельно работающими агрегатами и выборе состава работающего оборудования - часовых нагрузок. При решении задач прогнозирования годовых максимумов нагрузки или годовых уровней электропотребления обычно используются многочлены Y(t)=a0+a1t+a2t2+.... Возможно также прогнозирование в пространстве ортонормированных многочленов. Если Gn - многочлен порядка n -1, то
Y(t)=a0 G0(t)+a1 G1(t)+a2 G2(t)+.... В прогнозах на перспективу часто используются нелинейные математические модели, например Y(t)=a0-a1exp(-a2t). Моделирование месячных максимумов нагрузки выполняется на основе модели, учитывающей сезонные колебания прогнозируемого параметра Y(t)=a0+a1t+a2 cos (2 p t/T), где Т - период колебаний (например, равный одному году). Прогнозирование связей между выработкой электроэнергии и некоторыми показателями спроса на нее выполняется на основе эконометрических моделей множественной регрессии:
Выбор той или иной математической модели и оценка ее параметров осуществляются на основании некоторого критерия, зависящего от того, насколько точно теоретическая функция описывает статистический ряд. Одним из таких критериев является сумма квадратов отклонений эмпирических данных от теоретических оценок. После выбора критерия решается оптимизационная задача определения параметров математической модели, минимизирующих критерий. Метод наименьших квадратов Задача 3.2. Методом наименьших квадратов оценить коэффициенты { ai } полинома
интерполирующего заданный эмпирический временной ряд. Решение представлено в таблицах рис. 3.14, 3.15. В строке А23:Е23 задаются начальные значения параметров. В строке В27:К27 представлен ряд наблюдений. В строке 26 по формуле (3.6) вычисляются теоретические значения функции Y(t). Строка 28 представляет разность строк 26 и 27. В ячейке L28 записана формула =СУММКВ(B28:K28) расчета суммы квадратов отклонений теоретических значений от наблюдаемых. При оптимизации минимизируется значение ячейки L28 в ходе изменения содержимого ячеек А23:Е23. Исходная таблица оптимизации представлена на рис. 3.14. Результирующая – на рис. 3.15. В результате аппроксимирующая функция имеет вид y(t)=-2,52+7,51t+10,7t2+7,2cos(2πt/2,39). Отыскание параметров {ai} выполняется с помощью операции Сервис/Поиск решения. При этом сумма квадратов отклонений составляет 1,6, что свидетельствует о достаточно хорошем приближении теоретической функции. Соотношение теоретической кривой и экспериментальных данных представлено на рис. 3.16.
Рис. 3.14. Исходные параметры оптимизации
Рис. 3.15. Результирующая таблица наименьших квадратов
где Q(t) - полином, отражающий нециклический характер прогнозируемой величины; ak, bk, k =1,2,..- оцениваемые коэффициенты ряда.
Самостоятельная работа · Повторите на ЭВМ представленные расчеты. · Уберите последний член полинома и оцените погрешность интерполяции. · На базе только экспериментальных данных на графике ряда через тренд определите коэффициенты полинома третьего порядка, наилучшим образом (по методу наименьших квадратов) описывающего экспериментальный ряд. Оцените погрешность интерполяции. · На основе полученных данных получите значение анализируемой величины при t=1,1 (прогноз через экстраполяцию функции). Метод скользящего среднего В оперативных прогнозах электрических нагрузок и электропотребления необходимо учитывать циклическую составляющую, определяемую устойчивыми циклами природных (день, ночь, зима, лето) и социальных (рабочие, выходные и праздничные дни) явлений. В суточном разрезе нагрузка регулярно снижается в ночные часы и повышается в утренние и вечерние. В недельном разрезе регулярные снижения нагрузки имеют место в нерабочие дни. В годовом разрезе наблюдается снижение нагрузки в летний период (время летних отпусков и длинного светового дня).
Функционально циклическая составляющая может быть представлена некоторой периодической (сутки, неделя, год) функцией с нулевым средним значением. При этом прогноз может быть представлен в виде суммы нециклической R(t) (тренд), циклической S(t) и случайной e(t) составляющих Нулевая величина математического ожидания S(t) и e(t) подсказывает алгоритм решения задачи, который в литературе называется методом скользящего среднего. Определяется среднее статистическое значение анализируемой величины на интервале (t - T ц/2, t + T ц/2), где - T ц длительность цикла (12 месяцев, или 365 дней, или 8760 часов). Полученная величина присваивается нециклической составляющей R(t), которая называется трендом и моделируется, например, полиномом R * (t). Следующим этапом является анализ статистического ряда Zi={Yi -R*(ti)} и его моделирование циклической функцией S(t). Здесь математическая модель может быть совершенно иной, например ряд Фурье. Из остатка Zi- S(t i ) подобным образом можно выделить циклическую составляющую с меньшим периодом (неделя).
Линейный тренд
С целью иллюстрации метода построим ряд случайных чисел, имеющих линейный тренд и циклическую составляющую. Для ускорения процесса построения экспериментальной кривой начиная со второй строки в столбцах А (время) и В (функция) строим арифметические прогрессии, соответственно (1,2,…,26) и (5, 5.5, 6, …,17.5). Отобразим данные столбца В точечной диаграммой. На диаграмме выполняем циклические (цикл равен пяти временным интервалам) коррекции {оставить, приподнять, оставить, опустить, оставить} (рис. 3.17). Числовой ряд в столбце В также автоматически корректируется.
Циклическая составляющая (рис. 3.18) образуется вычитанием из исходного ряда теоретических значений тренда: Е4:Е25:=В4:В25-D4:D25. Индикатором правильности наших построений может служить сумма ряда Е4:Е25, близкая к нулю. В табл. 3.15 в транспонированном виде (для экономии места в тексте) частично представлен рассмотренный этап расчетов. Таблица 3.15
Самостоятельная работа · Представьте исходный (до коррекции) статистический ряд не прямой, а параболой. Выполните периодическую (0,1,1,0,-1,-1, где 1-увеличить, -1 – уменьшить, 0 – оставить без изменения) коррекцию ряда. Выполните аппроксимацию тренда кривой второго порядка. Представьте графическое изображение тренда и циклической составляющей. · Выполните аппроксимацию циклической составляющей рядом Фурье. · Выполните прогноз на 5 временных периодов. Вероятность и статистика Расчет режимов ЭЭС сводится, как правило, к определению напряжений в узлах электрической сети при заданных параметрах связей, активных и реактивных мощностях нагрузки и генерации, пределах изменения тех или иных величин и т.д. Однако насколько данный режим будет соответствовать реальному? Почти каждый из нас ответит - наверняка соответствовать не будет. Действительно, практически все заданные параметры являются случайными величинами. При этом случайной является и конфигурация ЭЭС (отключение тех или иных элементов). Инженеры-электрики это прекрасно осознают и большее внимание уделяют лишь характерным режимам (суточный максимум и минимум нагрузки, отключение генератора, трансформатора, электропередачи и др.). В то же время во многих задачах электроэнергетики, особенно в задачах перспективного развития, приходится учитывать вероятностный характер информации (состав оборудования, нагрузка ЭЭС в целом и по узлам, стоимость топлива, наличие инвестиций и др.). В данном разделе рассматриваются лишь примеры решения вероятностных задач в среде табличного процессора Excel.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 662; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.244.228 (0.014 с.) |

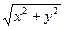 (модуль) комплексного числа. Пример: МНИМ.ABS("5+12i") равняется 13.
(модуль) комплексного числа. Пример: МНИМ.ABS("5+12i") равняется 13. , выраженный в радианах.
, выраженный в радианах.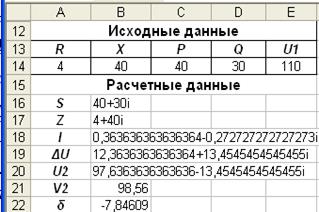 Посмотретьимеется ли в составе библиотечных функций категория “инженерные“ функции. Если нет, то необходимо подключить ее. В меню Сервис/Надстройки включите “ Пакет анализа ”. Снова проверьте наличие категории “инженерные “. Теперь она должна быть.
Посмотретьимеется ли в составе библиотечных функций категория “инженерные“ функции. Если нет, то необходимо подключить ее. В меню Сервис/Надстройки включите “ Пакет анализа ”. Снова проверьте наличие категории “инженерные “. Теперь она должна быть.  .
.

 Данный подход может быть использован для интерполяции (экстраполяции) временного ряда любой сложной функцией, например рядом Фурье:
Данный подход может быть использован для интерполяции (экстраполяции) временного ряда любой сложной функцией, например рядом Фурье: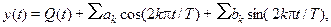
 . Случайная составляющая имеет также нулевое математическое ожидание. Отсюда задача анализа статистических данных сводится к определению каждой из указанных составляющих.
. Случайная составляющая имеет также нулевое математическое ожидание. Отсюда задача анализа статистических данных сводится к определению каждой из указанных составляющих. Благодаря специфике относительных адресов метод скользящего среднего достаточно просто реализуется в Excel.
Благодаря специфике относительных адресов метод скользящего среднего достаточно просто реализуется в Excel. Следующим этапом является выделение и аппроксимация тренда. Для этого в ячейке С4, соответствующей середине интервала цикла (t=3), записываем формулу усреднения данных на периоде: =СРЗНАЧ(B2:B6), которую распространяем до ячейки С25 (t=24). Предположим, что тренд моделируется линейной функцией y(t)=a0+a1t. Выделим ячейки для a 0, a 1, например Е1, Е2, где запишем начальные значения, например 1. В ячейках D4:D25 формируем ряд y(ti). В ячейке D27 формируем через формулу =СУММКВРАЗН(C4:C25;D4:D25) минимизируемую разность квадратов. В результате минимизации (Сервис/Поиск решения) получаем оценки коэффициентов a 0, a 1 и ряд значений теоретической функции.
Следующим этапом является выделение и аппроксимация тренда. Для этого в ячейке С4, соответствующей середине интервала цикла (t=3), записываем формулу усреднения данных на периоде: =СРЗНАЧ(B2:B6), которую распространяем до ячейки С25 (t=24). Предположим, что тренд моделируется линейной функцией y(t)=a0+a1t. Выделим ячейки для a 0, a 1, например Е1, Е2, где запишем начальные значения, например 1. В ячейках D4:D25 формируем ряд y(ti). В ячейке D27 формируем через формулу =СУММКВРАЗН(C4:C25;D4:D25) минимизируемую разность квадратов. В результате минимизации (Сервис/Поиск решения) получаем оценки коэффициентов a 0, a 1 и ряд значений теоретической функции.



