
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительная регрессионая статистикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Параметры se1,se2,...,sen, seb - стандартные значения ошибок для коэффициентов m 1, m 2,..., m n и для постоянной b (seb = #Н/Д, если параметр конст имеет значение ЛОЖЬ); r 2- коэффициент детерминированности (квадрат коэффициента корреляции). Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y; если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y; sey - стандартная ошибка для оценки y; F - F -статистика, или F -наблюдаемое значение. F - статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет; df - степени свободы. Степени свободы полезны для нахождения F -критических значений (распределение Фишера) в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F -статистикой, возвращаемой функцией ЛИНЕЙН(); ssreg - регрессионая сумма квадратов; ssresid - остаточная сумма квадратов.
Замечание. Если имеется только одна независимая переменная x, можно получить крутизну и y -пересечение непосредственно, используя функции НАКЛОН() и ИНДЕКС(ЛИНЕЙН(Y;X); 2) Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН(), зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН(). Когда имеется только одна независимая переменная x, m и b вычисляются по следующим формулам:
Функции аппроксимации ЛИНЕЙН() и ЛГРФПРИБЛ() могут вычислить прямую или экспоненциальную кривую, наилучшим образом описывающую статистические данные. Однако вам самим предстоит решать, какой из двух результатов лучше. Можно также вычислить функцию ТЕНДЕНЦИЯ() для прямой или функцию РОСТ () для экспоненциальной кривой. Эти функции, если не задавать аргумент Х, возвращают массив вычисленных значений y для фактических значений x в соответствии с прямой или кривой. Теперь можно сравнить вычисленные значения с фактическими. Можно также построить диаграммы для визуального сравнения.
Проводя регрессионный анализ, Excel вычисляет для каждой точки квадрат разности между прогнозируемым и фактическим значениями y. Сумма квадратов этих разностей называется остаточной суммой квадратов. Затем Excel подсчитывает сумму квадратов разностей между фактическими и средним значениями y, которая называется общей суммой квадратов (регрессионая сумма квадратов + остаточная сумма квадратов). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r 2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, описывает взаимосвязи между переменными. Следует заметить, что значения y, предсказанные с помощью уравнения регрессии, будут иметь меньшую точность, если они располагаются вне интервала значений y, который использовался для определения коэффициентов регрессии. Простая линейная регрессия Пример 1. Предположим, что фирма по продаже электрооборудования за первые шесть месяцев отчетного года имела доход на сумму 3100 руб., 4500 руб., 4400 руб., 5400 руб., 7500 руб. и 8100 руб. Пусть эти значения находятся в интервале ячеек B2:B7. Тогда можно использовать следующую простую линейную регрессионную модель для оценки объема продаж в девятом месяце. СУММ(ЛИНЕЙН(B2:B7)*{9;1}) равняется СУММ({1000;2000}*{9;1}) равняется 11 000 руб. Пример 2. Рассмотрим представленный в табл. 3.21 пример интерполяции временного ряда {yj} функцией
В результате На рис. 3.22 представлена экспериментальная функциональная зависимость и средствами графики получено уравнение тренда. Нетрудно видеть, что коэффициенты тренда практически совпадают с параметрами m,b (этого следовало ожидать, поскольку использовалась одна и та же функция).
Самостоятельная работа · Повторить предложенные расчеты. · Представить диаграмму, где были бы отражены минимальная и максимальная оценки линейной зависимости. · Изменением в столбце В снизить максимальное отклонение экперимента от тренда. Оценить изменение коэффициента детерминированности. Пример 3.Множественная линейная регрессия Рассмотрим представленный в табл. 3.22. пример интерполяции временного ряда { yj } функцией Таблица 3.21
Таблица 3.22
Решение получим с помощью функции ЛИНЕЙН(). Для этого представим интерполирующую функцию в виде многопараметрической зависимости
В ячейках F6:I10 записана формула =ЛИНЕЙН(A4:A13;B4:D13;;1). Использование F-статистики В предыдущем примере коэффициент детерминированности r 2 равен 0,78 (ячейка F8 в результатах функции ЛИНЕЙН()), что указывает на некоторую, не очень сильную зависимость между независимыми переменными и функционалом. Можно использовать F-статистику, чтобы определить, является ли этот результат (с таким значением r 2) случайным. Предположим, что на самом деле нет взаимосвязи между переменными, а просто были выбраны те случайные данные, для которых статистический анализ вывел показанную взаимозависимость. Допустимую вероятность (уровень значимости) ошибки гипотезы о том, что имеется значимая взаимозависимость, принято обозначать величиной α. Для оценки гипотезы используется так называемый F -критерий, который служит для проверки гипотезы о равенстве дисперсий ( Если F -наблюдаемое (ячейка F9) больше, чем F -критическое, то взаимосвязь между переменными и функционалом (трендом) является значимой. Величину
Из таблицы справочника F -критическое равно 4,76. Наблюдаемое F -значение равно 7,17, что больше 4,76. Следовательно, гипотеза о взаимосвязи линейной корреляции функционала и переменных не отвергается, и полученное регрессионное уравнение может быть использовано для прогнозирования нагрузки. Было бы неразумно окружать свое рабочее место толстыми математическими справочниками. Не поможет ли нам Excel получить F -критическое? Нет проблем. Для этого имеется встроенная функция FРАСПОБР(). Функция FРАСПОБР (α; v1; v2) возвращает обратное значение для F -распределения вероятностей (функция FРАСП(x;...)). Если α = FРАСП(x;...), то х = FРАСПОБР(α;...). Параметры v1, v2 - это числа степеней свободы. Замечания · ·Если число степеней свободыне целое число, то оно усекается до целой. · ·Функция возвращает значение ошибки #ЧИСЛО!, если вероятность α < 0 или α > 1, или v1, v2 < 1, или v1, v2 > 1010. Пример. FРАСПОБР(0,05;3;6) равняется 4,757. Вычисление t-статистики Другой гипотетический эксперимент определит, полезен ли каждый коэффициент наклона для оценки тренда мощности (см. табл. 3.22). Например, для проверки того, имеет ли статистическую значимость циклическая составляющая, разделим 554,81 (коэффициент пропорциональности при cos(p/5*t)) на 297,18 (оценка стандартной ошибки для коэффициента времени эксплуатации): t = m3/se3 = 554,81/ 297,18 = 1,846. Эта величина сопоставляется с t -критерием (распределение Стьюдента), который служит для сравнения двух средних значений из нормально распределенных генеральных совокупностей случайных величин в предположении, что равны их дисперсии. Если посмотреть в таблицу справочника по математической статистике, то окажется, что t -критическое с шестью степенями свободы и a = 0,1 равно 1,94. Поскольку абсолютная величина t, равная 1,846, меньше, чем 1,94, то можно сделать вывод о том, что циклическая составляющая - это незначимая переменная для оценки тренда мощности. Аналогичным образом можно протестировать на статистическую значимость все другие переменные. Как и для F -распределения, Excel имеет возможность вычислить t -критическое с помощью встроенной функции СТЬЮДРАСПОБР().
Функция СТЬЮДРАСПОБР (вероятность; df) возвращает обратное распределение Стьюдента для заданных вероятности, соответствующей двустороннему распределению Стьюдента, и числа степеней свободы df. Замечания · Если df не целое, то оно усекается до целой. · Если вероятность меньше нуля или больше единицы, или число степеней свободы меньше единицы, то функция СТЬЮДРАСПОБР() возвращает значение ошибки #ЧИСЛО!. · Рассматриваемая функцияиспользует итерационный метод для вычисления возвращаемого значения. Если итерационный процесс не сходится за 100 итераций, то функция возвращает значение ошибки #Н/Д. Пример. СТЬЮДРАСПОБР(0,1;6) равняется 1,94.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.215.122 (0.008 с.) |


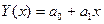 . Парные наблюдения (x,y) записаны соответственно в столбцах А и В. В блоке G2:H6 получены результирующие параметры функции ЛИНЕЙН(B2:В13;A2:A13;;1)
. Парные наблюдения (x,y) записаны соответственно в столбцах А и В. В блоке G2:H6 получены результирующие параметры функции ЛИНЕЙН(B2:В13;A2:A13;;1)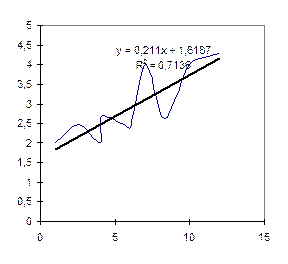 Рис. 3.22. Экспериментальная кривая и тренд
Рис. 3.22. Экспериментальная кривая и тренд
 . Эта функция для разных х представлена в столбце С. В соседнем столбце вычислена поэлементная разность теоретических и экспериментальных значений у. В ячейке D14 вычисляется сумма квадратов отклонений. Нетрудно видеть, что она полностью совпадает с результирующим параметром Sres (Н6). Стандартные ошибки для полученных коэффициентов позволяют оценить разброс y(x), т.е. получить, например, по критерию
. Эта функция для разных х представлена в столбце С. В соседнем столбце вычислена поэлементная разность теоретических и экспериментальных значений у. В ячейке D14 вычисляется сумма квадратов отклонений. Нетрудно видеть, что она полностью совпадает с результирующим параметром Sres (Н6). Стандартные ошибки для полученных коэффициентов позволяют оценить разброс y(x), т.е. получить, например, по критерию 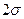 максимальную и минимальную оценку y(x) - столбцы I, J.
максимальную и минимальную оценку y(x) - столбцы I, J. .
. .
. ), при условии, что X и Y распределены нормально. В общем случае из каждой генеральной совокупности производятся выборки объемом n 1 и n 2. В качестве контрольной величины используется отношение эмпирических дисперсий
), при условии, что X и Y распределены нормально. В общем случае из каждой генеральной совокупности производятся выборки объемом n 1 и n 2. В качестве контрольной величины используется отношение эмпирических дисперсий  . Величина F удовлетворяет F -распределению (распределение Фишера) c v1 и v2 степенями свободы (v1= n 1-1, v2= n 2-1). В рассматриваемом случае в качестве сопоставляемых величин являются функционал и вектор параметров.
. Величина F удовлетворяет F -распределению (распределение Фишера) c v1 и v2 степенями свободы (v1= n 1-1, v2= n 2-1). В рассматриваемом случае в качестве сопоставляемых величин являются функционал и вектор параметров.


