Основы юридической статистики

Основы юридической статистики

Вопросы лекции

1. Понятие юридической статистики. 1

2. Первичная обработка материалов массовых статистических наблюдений 2

3. Графическое представление статистического распределения. 4

4. Числовые характеристики статистического распределения. 7

5. Ряды динамики. 9

5.1. Понятие о рядах динамики и их виды.. 9

5.2. Показатели, характеризующие тенденцию динамики. 12

5.3. Расчет параметров тренда. 14

5.4. Показатели колеблемости. 17

5.5. Прогнозирование на основе тренда и колеблемости. 18

6. Статистические взаимосвязи. 20

6.1. Функциональная и корреляционная зависимости. 20

6.2. Условия применения корреляционно-регрессионного анализа. 22

6.3. Задачи корреляционно-регрессионного анализа. 23

6.4. Парная линейная корреляция. 25

 

Понятие юридической статистики

Статистика – это общественная наука, изучающая количественную сторону массовых общественных явлений и процессов в неразрывной связи с их качественной стороной, в конкретных условиях места и времени.[1]

Массовые общественные явления и процессы представляют собой, например, производство и потребление товаров, внутреннюю и внешнюю торговлю, рождаемость и смертность, доходы и расходы населения и т.д. Каждое из этих явлений и процессов состоит из большого количества однородных единиц, которые вместе взятые в конкретных условиях места и времени представляют собой статистическую совокупность. Изучение статистической совокупности с учетом индивидуальности каждой ее единицы и составляет основную задачу статистической науки. Как отрасль практической деятельности статистика предполагает сбор, обработку, анализ и публикацию данных, характеризующих наблюдаемый объект. Статистика позволяет определить меру взаимосвязи между явлениями и процессами.

В основе статистической методологии лежит совокупность количественных и качественных приемов анализа изучаемых явлений и процессов. Она широко использует математику, как наиболее точный инструмент исследования.

Общая теории статистики является методологической наукой, которая разрабатывает и определяет общие принципы и методы статистического исследования.

Отраслевые статистики – статистика промышленности, труда, транспорта, юридическая статистика и т.д. используют методы общей статистики. Юридическая статистика – отрасль статистической науки, имеющая дело с количественными показателями правовой и иной юридически значимой деятельности.[2]

Числовые характеристики статистического распределения

Ряды динамики

Расчет параметров тренда

Понятие «тренд» было введено в статистику английским статистиком Гукером, которым он предложил обозначать уравнение тенденции.

Первым шагом в определении тренда необходимо выявить тип тенденции, а эта задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявление типа тенденции и требует всестороннего подхода к этой проблеме, прежде всего качественного изучения характера развития объекта. При этом необходимо учитывать условия развития объекта в изучаемом периоде и характер действия основных факторов развития.

В крупных системах, где действует большое количество факторов, резкие, скачкообразные изменения в ряду динамики крайне редки. Большие и сложные системы обладают значительной инерцией, и для скачкообразного, резкого изменения тенденции такой системы требуются большие затраты ресурсов. Напротив, в масштабе несложных систем вполне возможны резкие изменения, переходы от одной тенденции к другой.

Одним из основных типов уравнений тренда является линейная форма тренда:

где - уровни, освобожденные от колебании, выровненные по прямой;

b - начальный уровень тренда в момент или период, принятый за начало отсчета времени t;

a - среднегодовой абсолютный прирост (среднее изменение за единицу времени); константа тренда.

Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде.

Параметры тренда рассчитываются из следующих соотношений:

Если поместить начало отсчета в середину динамического ряда, то åt будет равняться нулю и формулы существенно упростятся:

, .

 

В статистических исследования используются и другие формы трендов – параболические, экспоненциальные, логарифмические, степенные, гиперболические и логистические. Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного развития, например снятии ограничений. Экспоненциальный тренд выражает тенденцию ускоренного (замедленного) и все более ускоряющегося (замедляющегося) возрастания уровней. Развитие любого объекта по экспоненциальному закону может продолжаться только небольшой исторический период времени, ибо ресурсы для любого процесса развития всегда встретят ограничения. Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного возможного значения. Замедление роста становится все меньше и меньше, и при достаточно большом t логарифмическая кривая становится мало отличимой от прямой линии. Логарифмический тренд пригоден для отображения эффективности системы при ее совершенствовании без качественных, коренных преобразований. Степенная форма - гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Гиперболический тренд выражает тенденцию замедляющегося снижения (или роста) уровня, стремящегося к некоторому пределу.

Логистическая кривая имеет форму латинской буквы S положенной на бок, отчего еще называется S-образной кривой. Она имеет два перегиба: от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость).

Устойчивость тенденции можно оценить с помощью коэффициента корреляции рангов Ч. Спирмена, который считается по формуле:

.

При полном совпадении (полной противоположности) рангов уровней и номеров периодов по их хронологическому порядку коэффициент Спирмена равен +1 (-1), что соответствует полной устойчивости возрастания (убывания) уровней.

Пример 5. Определим устойчивость тенденции по данным из таблицы 6 - числа зарегистрированных преступлений, связанных с незаконным оборотом наркотиков в Российской Федерации (в единицах) за год с 1996г. по 2010 г. Промежуточные результаты оформим в виде следующей таблицы.

 

Таблица 8

 

Расчетное значение коэффициента корреляции по рангам составит:

, что свидетельствует о слабой устойчивости наблюдаемой тенденции и довольно сильной колеблемости.

Показатели колеблемости

Изучение колебаний уровней динамического ряда имеет важное значение для анализа и регулирования сезонных социальных процессов. Различают три основных типа колебаний.

Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней от тренда в одну и в другою сторону (рис. 5).

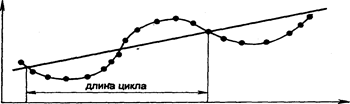
Рис. 5. Пилообразная колеблемость

Циклическая долгопериодическая колеблемость состоит в том, что отклонения уровней от тренда сначала постепенно увеличиваются, затем постепенно уменьшаются, и меняя свой знак на противоположный вновь начинают увеличиваться (рис. 6). Такая колеблемость свойственна, например, солнечной активности и связанными с ней процессами на Земле.

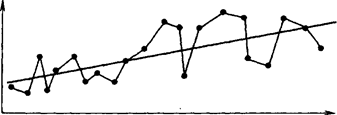
Рис. 6. Циклическая долгопериодическая колеблемость

Случайно распределенная во времени колеблемость возникает при наложении нескольких колебаний с различными циклами, но может проявляться в результате хаотичных колебаний основного действующего фактора (рис. 7).

Рис. 7. Случайно распределенная во времени колеблемость

Основными показателями силы колебания уровней являются: амплитуда отклонений уровней отдельных периодов или моментов от тренда, среднее абсолютное отклонение уровней от тренда, среднеквадратическое отклонение уровней от тренда. Относительное линейное отклонение от тренда и коэффициент колеблемости вычисляются путем деления соответствующих абсолютных показателей на средний уровень за весь изучаемый период.

Среднее линейное отклонение вычисляется из соотношения:

,

где yi – фактический уровень;

- выровненный уровень (тренд);

n – число уровней;

p – число параметров тренда (для линейной формы тренда p=2).

Среднеквадратическое отклонение вычисляется из соотношения:

.

Статистические взаимосвязи

Парная линейная корреляция

Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция. Подобные системы встречаются в тех случаях, когда среди всех действующих факторов выделяется один важнейший, который и определяет вариацию результативного признака, а нелинейные формы связей без особого ущерба могут быть преобразованы в линейные.

Зависимость , называется уравнением регрессии y по x или линейной корреляционной зависимостью между y и x.

где – среднее значение результативного признака Y при определенном значении факторного признака X;

b – свободный член уравнения;

а – коэффициент регрессии, характеризующий вариацию Y, приходящуюся на единицу вариации X.

Коэффициенты уравнения регрессии рассчитываются по методу наименьших квадратов.

Параметр a определяется из соотношения

,

где – среднее значение случайной величины x×y;

и – средние значения факторного и результативного признаков соответственно;

s_x – среднее квадратичное отклонение признака X;

x_i и y_i - индивидуальные значения соответствующих признаков.

Параметр b выражают из уравнения регрессии и вычисляют, подставляя средние значения признаков X и Y и найденное значение параметра а:

.

При парной связи ее теснота измеряется с помощью коэффициента корреляции:

Соотношение между значением модуля коэффициента корреляции и теснотой связи представлено в таблице 10.

Таблица 10

Значение модуля коэффициента корреляции	Характер связи
0,00 – 0,30	крайне слабая или отсутствует
0,30 – 0,50	слабая
0,50 – 0,70	средняя
0,70 – 0,99	сильная

 

Рассматривая возможные значения коэффициента корреляции, следует учитывать, что нулевая величина этого коэффициента соответствует полному отсутствию какой-либо связи. Это возможно при полном взаимном погашении положительных и отрицательных отклонений признаков от их средних величин. Поскольку вероятность этого крайне мала для любой реальной совокупности, кроме бесконечно большой, то коэффициент корреляции для реальной совокупности отличен от нуля и при отсутствии связи!

Значение коэффициента корреляции, равное 1 (или -1) соответствует функциональной связи. Чем ближе связь к функциональной, тем ближе абсолютная величина коэффициента корреляции к единице. Отрицательное значение коэффициента корреляции свидетельствует об обратной зависимости.

Значение коэффициента корреляции можно посчитать с помощью функции КОРРЕЛ, встроенной в табличном процессоре MS Excel, это облегчит рутинные математические подсчеты. Так же в MS Excel можно построить на графике и эмпирическую ломаную, и уравнение регрессии.

Пример 7. Определение корреляции между числом преступлений, связанных с незаконным оборотом наркотиков, в Новосибирской и Омской областях (данные взяты с официального сайта Федеральной службы государственной статистики РФ www.gks.ru и приведены в таблице 11 (в ед., значение показателя за год)).

Таблица 11.

Можно изобразить графически динамические ряды данного вида преступлений в Новосибирской и Омской области (см. рис. 9).

Рис. 9. Динамика преступлений, связанных с незаконным оборотом наркотиков в Новосибирской и Омской областях

Проанализировав график, можно предположить, что эти данные будут коррелировать между собой. Рассчитав коэффициент корреляции, получаем, что , это означает, что корреляционная связь между признаками прямая и сильная. Изобразим графически эмпирические данные и построим прямую регрессии. Табличный процессор MS Excel позволяет нам автоматически строить прямую регрессии и указывать ее уравнение на диаграмме.

Рис. 10. Корреляционная зависимость числа преступлений, связанных с незаконным оборотом наркотиков Новосибирской и Омской областях

 

[1] См.: Лялин В. С. Правовая статистика: учебник / В. С. Лялин, Е. А. Костыря; Санкт-Петербург. ин-т внешнеэконом. связей, экономики и права, О-во "Знание" Санкт-Петербурга и Ленинград. обл. - СПб. 2006. С. 9.

[2] См.: Лунеев В. В. Юридическая статистика: учебник / В. В. Лунеев; Акад. правовой ун-т, Ин-т государства и права Рос. акад. наук. - М.: Юристъ, 2000. С. 23.

 

[3] http://www.gks.ru/wps/wcm/connect/rosstat/rosstatsite/main/population/infraction/.

 

[4] См.: Лунеев В. В. Юридическая статистика: учебник / В. В. Лунеев; Акад. правовой ун-т, Ин-т государства и права Рос. акад. наук. - М.: Юристъ, 2000. С. 307.

[5] См.: Лунеев В. В. Юридическая статистика: учебник / В. В. Лунеев; Акад. правовой ун-т, Ин-т государства и права Рос. акад. наук. - М.: Юристъ, 2000. С. 287.

[6] Чупров Александр Александрович - русский статистик (1874-1926).

[7] Елисеева И.И., Юзбашев М.М. Общая теория статистики. -М.:Финансы и статистика, 1998.

[8] Крастинь О.П. Разработка и интерпретация моделей корреляционных связей в экономике. — Рига: Зинатне, 1983.

[9] Стюдент (student) – псевдоним английского математика и статистика Вильяма Госсета (1876 - 1937).

[10] Карл Фридрих Гаусс – немецкий математик, физик и астроном (1777-1855).

Основы юридической статистики

Вопросы лекции

1. Понятие юридической статистики. 1

2. Первичная обработка материалов массовых статистических наблюдений 2

3. Графическое представление статистического распределения. 4

4. Числовые характеристики статистического распределения. 7

5. Ряды динамики. 9

5.1. Понятие о рядах динамики и их виды.. 9

5.2. Показатели, характеризующие тенденцию динамики. 12

5.3. Расчет параметров тренда. 14

5.4. Показатели колеблемости. 17

5.5. Прогнозирование на основе тренда и колеблемости. 18

6. Статистические взаимосвязи. 20

6.1. Функциональная и корреляционная зависимости. 20

6.2. Условия применения корреляционно-регрессионного анализа. 22

6.3. Задачи корреляционно-регрессионного анализа. 23

6.4. Парная линейная корреляция. 25