Графическое представление статистического распределения

Статистические таблицы высокоинформативны, но проникновение в их цифровое содержание требует времени. Большей наглядностью обладают графики, составленные на основе табличных данных. Графическое изображение даже самых сложных статистических показателей делает их не только наглядными, но доходчивыми и понятными с первого взгляда. График позволяет быстро уловить важнейшие тенденции и закономерности изучаемого явления.

В статистических графиках обычно применяется система прямоугольных координат в двумерном или трехмерном изображении с заданным масштабом. В статистических графиках, как правило, применяются прямолинейные масштабные шкалы. В связи с этим на осях абсцисс и ординат в условных масштабах откладываются соответствующие единицы измерения. График должен иметь заголовки и словесные пояснения. Он обязательно должен содержать наименования масштабных шкал: название отложенных на них единиц измерения и другие необходимые пояснения.

В зависимости от целей графика, его количественной базы и применяемых геометрических знаков графики могут быть точечными (совокупность точек), линейными, столбиковыми, полосовыми, квадратными, круговыми и т. д.

Линейные графики имеют широкое распространение в уголовно-правовой и криминологической статистике для изображения динамики преступности, осужденных, заключенных и т. д.

Секторные диаграммы наглядно раскрывают структуру явления и структурные сдвиги в нем в зависимости от территории, времени и других обстоятельств. Данные диаграммы строятся в виде круга, разделенного на отдельные сектора, каждый из которых характеризует какую-то часть целого явления и занимает площадь круга пропорционально удельному весу этой части, которая принимается за 100%. Пример такой диаграммы (построенной по данным с официального сайта Федеральной службы государственной статистики РФ www.gks.ru[3] изображен на рисунке 1.

 

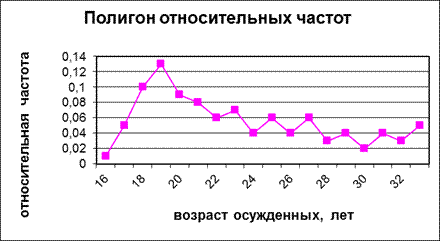
Рис. 1. Структура преступности в РФ

Для графического изображения статистического распределения пользуются полигонами, гистограммами, кумулятами и огивами.

Для построения полигона частот (относительных частот) на оси ОX откладывают значения вариант х_i, на оси ОY- значения частот n_i (относительных частот ).

Пример 2. Полигон относительных частот статистического распределения по возрасту 100 преступников – рецидивистов (таблица 2).

Рис. 2. Полигон относительных частот

Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал разбивают на несколько частичных интервалов и находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i -ый интервал. Затем вычисляют отностительные частоты на каждом интервале по формулам: , и плотности частот по формулам: , где m – длина интервала. Затем на этих интервалах, как на основаниях, строят прямоугольники с высотами, равными плотностям. Таким образом, площади прямоугольников равны соответствующим относительным частотам.

Пример 3. В таблице 4 представлен интервальный вариационный ряд с усредненными показателями для многих стран[4], который отражает связь между варьирующим возрастом и изменением частот (процентами лиц, совершивших преступления).

Таблица 4

Возраст, лет	До 15	16-20	21-25	26-30	31-35	36-40	41-45	46-50	51-60
Преступле­ния, %

Построим гистограмму данного статистического распределения.

Рис. 3. Гистограмма

 

По данным мировой, российской и региональной статистики наблюдается практически одна и та же тенденция распределения правонарушителей по возрасту: с начала возраста уголовной ответственности идет рост преступной активности, в 25—30 лет (с некоторыми колебаниями) ее уровень достигает апогея, а затем наступает постепенное снижение. В этом проявляется определенная закономерность изменения частот в вариационных рядах, называемая закономерностью распределения, которая выявляется в больших совокупностях, где случайные отклонения взаимоуничтожаются.

Графические представления статистического распределения широко используются при выдвижении гипотезы о соответствии наблюдаемых характеристик тому или иному закону распределения, в этом и заключается основная суть анализа вариационных рядов