
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет сети постоянного токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математический метод. Уравнения узловых напряжений в матричном виде для сети постоянного тока из n независимых (без балансирующих) узлов имеют следующее представление:
где Y - матрица проводимостей;
Задача 3.1 Определить напряжения в узлах электрической сети (рис. 3.7). Решение может быть найдено по макету табл. 3.5. Формульное представление расчетных величин отображено в табл.3.6. Таблица 3.5
Таблица 3.6
Самостоятельная работа · Выполните представленный расчет режима электрической сети. · Под матрицей Y получите обратную матрицу Y-1. Проверьте правильность расчетов (произведение матриц YY-1 дает единичную матрицу). Получите вектор напряжений с помощью обратной матрицы. · Включите между узлами 2-4 связь с сопротивлением 4 Ом иповторите расчеты.
· Методом подбора параметра (Сервис/Подбор параметра) получите такое напряжение первого базового узла, чтобы напряжение узла 4 было бы равно 8 кВ. · С помощью таблиц подстановок получите функцию изменения напряжения в узле 4 от напряжения первого базового узла (в диапазоне (8-12) с шагом DU=0,5). Аналогично - для второго базового узла. Совместите полученные функции на одном графике. Какой делается вывод? Расчет токов трехфазного короткого замыкания Метод Z-матрицы Для расчета токов трехфазного короткого замыкания часто используется метод Z-матрицы. Матрица узловых сопротивлений является обратной по отношению к матрице узловых проводимостей Z=Y-1. Если базовый узел является источником питания, то диагональные элементы { Zkk } характеризуют эквивалентное сопротивление между источником питания и соответствующим узлом схемы. Действительно, в уравнении для напряжения узла i
элемент Zij = D Ui /D Jj определяет изменение напряжения в узле i при изменении тока в узле j, а Zkk = D Uk /D Jk - изменение напряжения в узле k при изменении тока в этом же узле, т.е. является эквивалентным сопротивлением между узлом k и источником питания (базисный узел). Отсюда величина тока КЗ в узле k должна быть такой, чтобы напряжение в этом узле стало равным нулю, т.е. D Uk = Uk - Ub= При решении поставленной задачи следует предусмотреть место для матриц Y и Z, где Z является расчетной матрицей. Для выделения диагонали (вектор-столбец) матрицы Z предлагается следующий эффективный в Excel прием. Строится единичная матрица Е такой же размерности, что и матрица Z. В первом элементе результирующего столбца вычисляется сумма произведений соответствующих элементов первых строк матриц Z и Е. Далее формула копируется на остальные строки. Математически для строки k данная операция представляется через скалярное произведение строк матриц Z и Е: dk =(Zk,Ek), k= 1 ,…,n. Полученный столбец-диагональ D можно использовать для вычисления результирующих токов КЗ (табл. 3.7, схема - рис. 3.7, где Ub=100 (одинаково для обоих источников питания)). В ячейке L18 записана формула "=СУММПРОИЗВ(B18:E18;G18:J18)". В ячейке М18 записана формула " =-$G$13/L18". Подобные формулы, полученные через копирование, записаны в L19:М21. Таблица 3.7
· Выполните расчеты по приведенному образцу Остаточные напряжения определяются через отклонения напряжения от базисного
Строка 23 формируется путем транспонирования результирующего столбца токов КЗ (JКЗ из табл. 3.7). В блоке Н24: К24 записана формула "=$G$13+B18:E21*$H$23:$K$23", где в ячейке G13 содержится U b, блоки B18:E21 и *$H$23:$K$23 – соответственно матрица Z и вектор токов КЗ. Представляет интерес представленное в формуле произведение массивов. В результате выполнения операции * каждый столбец матрицы Z умножается на соответствующее значение тока КЗ. Поскольку в результате формируется массив, то конструирование формулы заканчивается комбинацией из трех клавиш – Ctrl+Shift+Enter. Аналогичным образом можно почленно умножать матрицы одинакового размера, матрицу на столбец. · Выполните расчеты по приведенному образцу Распределение токов по ветвям выполняется с помощью взаимных элементов матрицы Z, которые по своему физическому смыслу определяют изменение напряжения в одном узле при изменении тока в другом
Разности Расчет распределения токов по ветвям для рассматриваемой схемы приведен в табл. 3.8, где отдельно выделено вычисление матрицы разностей { Блок D39:G44 формируется с помощью формулы =МУМНОЖ(C30:H35;B18:E23) (умножение матрицы инциденций М на расширенную матрицу Z* (расширение нулями)). Блок I39:L44 вычисляется по формуле =D39:G44*$D$46:$G$46/$C$39:$C$44, отражающей умножение разностей
Таблица 3.8
· Выполните расчеты по приведенному образцу Представляет интерес дополнительный расчет. В результате умножения транспонированной матрицы инциденций на полученную матрицу распределения токов будет вычислена матрица, диагональные элементы которой с точностью до знака представляют токи КЗ в узлах, а строки, соответствующие базовым узлам, характеризуют распределение токов между источниками питания (табл. 3.9). Таблица 3.9.
Эквивалентирование сети
Дальнейшие расчеты токов КЗ выполняются с помощью достаточно хорошо представленных в литературе индивидуальных кривых затухания, которые, при желании, в табличном виде можно представить на отдельном листе рабочей книги Excel.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.232.244 (0.011 с.) |

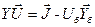 ,
,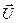 - вектор напряжений;
- вектор напряжений; 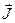 -вектор узловых токов (ток нагрузки положителен, а генерации - отрицателен),
-вектор узловых токов (ток нагрузки положителен, а генерации - отрицателен), 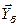 - вектор проводимостей ветвям, связанных с базой; U б - напряжение базисного узла. Базисных узлов может быть несколько, с разными напряжениями. Решение представленного матричного уравнения имеет вид
- вектор проводимостей ветвям, связанных с базой; U б - напряжение базисного узла. Базисных узлов может быть несколько, с разными напряжениями. Решение представленного матричного уравнения имеет вид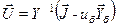 .
. Задача заключается в определении напряжений при заданных схеме электрической сети, сопротивлениях (проводимостях) ветвей схемы, узловых токах и напряжениях базисных узлов.
Задача заключается в определении напряжений при заданных схеме электрической сети, сопротивлениях (проводимостях) ветвей схемы, узловых токах и напряжениях базисных узлов. «функции» в левой части формульной строки вызывается вторая функция МОБР(), где указывается блок B3:E6. Здесь, не нажимая [ ОК ], щелкните ЛК мыши в конце формулы формульной строки. Появляется предыдущая панель функции МУМНОЖ(), где во второй строке указывается блок K3:K6. Не нажимая [ ОК ], нажмите три клавиши Ctrl+Shift+Enter.
«функции» в левой части формульной строки вызывается вторая функция МОБР(), где указывается блок B3:E6. Здесь, не нажимая [ ОК ], щелкните ЛК мыши в конце формулы формульной строки. Появляется предыдущая панель функции МУМНОЖ(), где во второй строке указывается блок K3:K6. Не нажимая [ ОК ], нажмите три клавиши Ctrl+Shift+Enter.
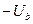 ,
, 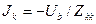 .
.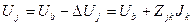 .
.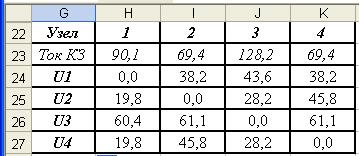 Расчет остаточных напряжений предлагается выполнять по макету рис. 3.8, где отдельные столбцы (H, I, J, K) соответствуют точкам КЗ (узлы 1, 2, 3, 4).
Расчет остаточных напряжений предлагается выполнять по макету рис. 3.8, где отдельные столбцы (H, I, J, K) соответствуют точкам КЗ (узлы 1, 2, 3, 4).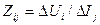 (имеют, как и диагональные элементы, отрицательные значения). Тогда при КЗ в точке k ток по ветви i-j определяется соотношением
(имеют, как и диагональные элементы, отрицательные значения). Тогда при КЗ в точке k ток по ветви i-j определяется соотношением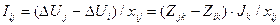 .
.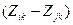 могут быть вычислены с помощью матрицы инциденций М, число строк которой равно числу ветвей, а столбцов - числу узлов. Для ветви i-j в столбце узла i ставится +1, а в столбце узла j - -1. Электрической сети (см. рис. 3.7.) соответствует матрица М, представленная на рис. 3.9. В результате умножения R=MZ * матрицы инциденций М на расширенную матрицу Z * (снизу добавляются нулевые строки, по числу базовых узлов) получается матрица разностей сопротивлений R (число строк равно числу ветвей, а столбцов - числу узлов КЗ). Действительно, в результате умножения строки, соответствующей ветви i-j, на k -й столбец будет получена величина
могут быть вычислены с помощью матрицы инциденций М, число строк которой равно числу ветвей, а столбцов - числу узлов. Для ветви i-j в столбце узла i ставится +1, а в столбце узла j - -1. Электрической сети (см. рис. 3.7.) соответствует матрица М, представленная на рис. 3.9. В результате умножения R=MZ * матрицы инциденций М на расширенную матрицу Z * (снизу добавляются нулевые строки, по числу базовых узлов) получается матрица разностей сопротивлений R (число строк равно числу ветвей, а столбцов - числу узлов КЗ). Действительно, в результате умножения строки, соответствующей ветви i-j, на k -й столбец будет получена величина 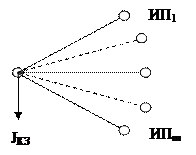 Для учета индивидуального характера изменения во времени периодической составляющей ТКЗ от разных источников питания (ИП) сложная схема электрической сети преобразуется к многолучевой схеме (рис. 3.10). Последняя таблица
Для учета индивидуального характера изменения во времени периодической составляющей ТКЗ от разных источников питания (ИП) сложная схема электрической сети преобразуется к многолучевой схеме (рис. 3.10). Последняя таблица 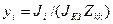 .
.


