
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальное распределение нагрузкиСодержание книги
Поиск на нашем сайте
Предлагаемая задача базируется на рассмотренном выше программном модуле интерполяции. Грубым (без учета потерь мощности и сетевых ограничений) критерием оптимального распределения нагрузки между параллельно работающими агрегатами является равенство их относительных приростов Характеристика относительных приростов агрегата (ХОП) Таблица 4.8
Табличное решение задачи заключается в том, что для одной и той же шкалы относительных приростов строятся ряды мощностей, которые затем суммируются для получения ХОП системы в целом. Для заданного значения нагрузки по ХОП системы вычисляется соответствующий относительный прирост, по которому определяются генерации всех агрегатов. Полученная нами функция линейной интерполяции незаменима как на первом этапе - адаптации ХОП к шкале относительных приростов, так и на втором - распределении нагрузки между агрегатами. В табл. 4.9 показано построение ХОП системы из двух агрегатов с единой шкалой ОП и временное распределение нагрузки между агрегатами.
Таблица 4.9
В ячейке С13 записана формула "=lin_interpolation($B$3:$B$7;$A$3:$A$7;B13)", (см. табл. 4.8). Здесь следует отметить, что блоки $B$3:$B$7, $A$3:$A$7 записываются в абсолютной адресации, в то время как ссылка В13 на параметр - в относительной адресации (для последующего копирования формулы). В ячейке Н13 записана формула =lin_interpolation($E$13:$E$21;$C$13:$C$21;G13).
Здесь в качестве блока параметров представлен ряд мощностей системы, в качестве функционального блока - ряд мощности агрегата, а аргументом является текущая мощность нагрузки. Самостоятельная работа · Добавить к представленной модели еще два- три агрегата и получить решение задачи. · Построить графики ОП агрегатов. Функции комплексных чисел При работе в среде электронной таблицы при подключении пакета анализа становится доступным ряд функций комплексных чисел (разд. 3.6). Однако в среде Visual Basic эти функции не всегда доступны. Кроме того, для электрика желательно иметь набор функций операций с матрицами в среде комплексных чисел. С целью обучения составим пакет некоторых функций комплексных чисел. Функция Compl, получения комплексного числа В Excel комплексное число записывается в виде текстовой строки, скомпонованной из действительной и мнимой составляющих. В приведенной ниже программе следует обратить внимание на организацию индекса, который можно задавать или не задавать (по умолчанию индекс равен " i "). В списке параметров используется ключевое слово Optional, после которого параметр index имеет тип Variant, а не String. Проверка наличия параметра осуществляется функцией IsMissing(index). Поскольку в процессе расчетов могут быть получены числа в экспоненциальной форме, а в представлении комплексного числа не желательны дополнительные буквенные символы (Е), в программе применяется функция Format, преобразующая числа к виду "целая - дробная части", при этом назначается число знаков после запятой. Рекомендуем обратить внимание на данную функцию - ее использование бывает часто полезным. Для преобразования действительного числа в строку используется функция Str$(): Rem Получение комплексного числа Public Function compl(Re As Single, Jm As Single, Optional index) As String Re = Format(Re, "#.000000"): Jm = Format(Jm, "#.000000") If IsMissing(index) Then index = "i" 'проверка: задан ли index? If Jm < 0 Then s$ = "" Else s$ = "+" s$ - это строковая переменная compl = str$(Re) & s$ & str$(Jm) & index End Function
Действительная составляющая комплексного числа (функция ReCompl) Разделителем действительной и мнимой частей комплексного числа, записанного в виде текстовой строки, является знак "+" или "-". Отсюда следует определить местоположение этого символа и левую часть строки рассматривать как строковое представление действительной части. В приведенном ниже модуле используются функции Mid$(strl, k, l) - выделения l символов строки str, начиная с позиции k, и Val(str) - преобразования строки в число. Обратите внимание на конструкцию цикла Do Until …Loop.
Rem Действительная часть комплексного числа Public Function Recompl(compl As String) As Single k = 2 Do Until Mid$(compl, k, 1) = "+" Or Mid$(compl, k, 1) = "-" Or k > Len(compl) k = k + 1 Loop Recompl = Val(Mid$(compl, 1, k - 1)) End Function Самостоятельная работа · Выполните отладку предложенных функций. · Разработайте и выполните отладку функций, указанных в табл.4.10.
Таблица 4.10
Примечание. При построении каждой новой функции используйте уже отлаженные разработанные вами процедуры
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.184 (0.008 с.) |

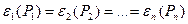 при условии, что в каждый момент времени их суммарная генерация равна мощности нагрузки
при условии, что в каждый момент времени их суммарная генерация равна мощности нагрузки 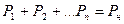 .
.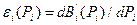 является, как правило, кусочно-линейной функцией, причем с относительно небольшим числом изломов (табл. 4.8).
является, как правило, кусочно-линейной функцией, причем с относительно небольшим числом изломов (табл. 4.8).


