
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет вероятностного режима электрической сетиСодержание книги
Поиск на нашем сайте Задача 3.3. Вероятностные параметры нагрузок
Таблица 3.16
Графики нагрузок (как случайных величин) и расчет искомых величин (математических ожиданий, дисперсий и корреляционных моментов нагрузок ЭЭС) представлены в табл. 3.16, где блок В3:D8 представляет статистическую выборку наблюдаемых величин, в ячейках В10, В11 записаны соответственно формулы =СРЗНАЧ(B3:B8), В11:=ДИСПР(B3:B8). Блоки С10:С11, D10:D11 является копированием В10:В11. Матрица корреляционных моментов строится следующим образом По диагонали записываются формулы F3, G4, H5: =КОВАР($B$3:$B$8;B3:B8); =КОВАР(C3:C8;$C$3:$C$8); =КОВАР($D$3:$D$8;D3:D8). Ячейки справа и слева заполняются копированием соответствующих строчных диагональных элементов. Диагональматрицы ковариаций состоит из дисперсий, в чем нетрудно убедиться (см. табл. 3.16, В11:D11). Получение матрицы коэффициентов корреляции можно выполнить по аналогии с построением матрицы корреляционных моментов (F8: =КОРРЕЛ($B$3:$B$8;B3:B8)), но если матрица { Кij } существует, то проще матрицу { rij } получить, исходя из определения (3.8) с помощью дополнительной матрицы перекрестных произведений S=sts, где s- вектор- строка среднеквадратических отклонений. Элемент матрицы Самостоятельная работа · Выполните приведенные тестовые расчеты табл. 3.16, формируя матрицу коэффициентов корреляции как первым, так и вторым способом. · Получите матрицу коэффициентов корреляции методом перекрестных произведений. Методические указания. В ячейках B14:D19 постройте дополнительную центрированную матрицу статистических данных, например, по формуле {=B3:D8-B10:D10}. Корреляционная матрица определяется произведением транспонированной новой матрицы на новую матрицу, деленную на число элементов ряда. Задача 3.4. Расчет потерь энергиив заданной (см. рис. 3.19) электрической сети. Потери мощности в линии, связывающей узлы i и j сети постоянного тока, имеющей проводимость Yij, рассчитываются по формуле Для расчетов потерь в вероятностном пространстве функция
где частные производные берутся в точке Потери энергии
Данная формула показывает, что величина потерь полностью определяется двумя характеристиками случайного вектора напряжений: его математическим ожиданием и матрицей корреляционных моментов. В простейшем случае составляющая
где При некоторых допущениях
где Расчет потерь энергиив заданной (см. рис. 3.19) электрической сети целесообразно выполнять на том же листе, где представлены расчеты вероятностных параметров (Задача 3.3). Сопротивления связей определены в табл. 3.17. Расчет потерь энергии на основе упомянутого упрощенного выражения (3.10) представлен в табл. 3.18. Таблица 3.17
Блок А18: С20 представляет матрицу проводимостей. Рядом записывается столбец проводимостей на базу (для получения расширенной матрицы проводимостей). Блок E18: G20 получен обращением матрицы Y. В блоке А24:А27 записывается расширенный вектор напряжений (исходные значения Ui=UБ) - определяется методом наименьших квадратов невязок токов. Рядом формируется транспонированный вектор математических ожиданий мощностей, полученных на предыдущем этапе (Задача 3.3). Величины в блоке С24:С26 получены умножением расширенной матрицы проводимостей на расширенный вектор напряжений. Массив D24:D26 определяет токи в узлах (поэлементное деление мощности на напряжение). Вектор справа - небаланс токов в узлах. В ячейке Е28 формируется сумма квадратов невязок токов. Процедурой Данные/Поиск решения этот небаланс минимизируется путем изменения вектора напряжений А24:А26 (на табл. 3.18 представлено оптимальное решение). Таблица 3.18
Потери мощности, соответствующие математическим ожиданиям напряжений (первая составляющая), определяются разностью потока мощности
Определение суммарных потерь мощности и суточных потерь энергии не представляет затруднений. Самостоятельная работа · Выполните представленные тестовые расчеты · Выполните уточненный расчет потерь энергии (с учетом (3.9)) для рассматриваемой сети. Определите погрешность упрощенной модели.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 Электрическая сеть, показанная на рис. 3.19, связывает районы потребления, нагрузки и генерация которых являются случайными величинами. Однако узловые мощности коррелированны, поскольку они в одинаковой степени подвержены жизненным циклам (день, ночь, суббота, воскресенье, с увеличением нагрузки растет и генерация и др.). Для прогноза электрического режима требуется оценить вероятностные параметры электрических величин.
Электрическая сеть, показанная на рис. 3.19, связывает районы потребления, нагрузки и генерация которых являются случайными величинами. Однако узловые мощности коррелированны, поскольку они в одинаковой степени подвержены жизненным циклам (день, ночь, суббота, воскресенье, с увеличением нагрузки растет и генерация и др.). Для прогноза электрического режима требуется оценить вероятностные параметры электрических величин. . Вычисление { rij } реализуется поэлементным делением массивов ковариаций на
. Вычисление { rij } реализуется поэлементным делением массивов ковариаций на  (в блоке F8:H10 записана формула {=E3:G5/МУМНОЖ(ТРАНСП(B12:D12);B12:D12))}. Такой прием особенно ценен при большой размерности матрицы ковариаций; его следует принять на вооружение, поскольку перекрестные произведения часто встречаются в иных технических приложениях.
(в блоке F8:H10 записана формула {=E3:G5/МУМНОЖ(ТРАНСП(B12:D12);B12:D12))}. Такой прием особенно ценен при большой размерности матрицы ковариаций; его следует принять на вооружение, поскольку перекрестные произведения часто встречаются в иных технических приложениях.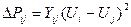 - произведение тока на разность потенциалов. Потери мощности по всей сети определяются суммированием потерь по ветвям
- произведение тока на разность потенциалов. Потери мощности по всей сети определяются суммированием потерь по ветвям 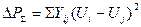 . В таком виде потери функционально зависят от напряжений, в то время как основной случайный параметр - нагрузка в узлах. Кроме того, представленная формула пригодна для единичной реализации режима электрической сети, а не генеральной совокупности режимов.
. В таком виде потери функционально зависят от напряжений, в то время как основной случайный параметр - нагрузка в узлах. Кроме того, представленная формула пригодна для единичной реализации режима электрической сети, а не генеральной совокупности режимов. представляется в окрестности точки математических ожиданий напряжений
представляется в окрестности точки математических ожиданий напряжений  рядом Тейлора
рядом Тейлора ,
, , а
, а  представляет отклонение напряжения от математического ожидания
представляет отклонение напряжения от математического ожидания 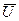 (напряжения узлов являются случайными величинами, поскольку они зависят от случайных узловых мощностей).
(напряжения узлов являются случайными величинами, поскольку они зависят от случайных узловых мощностей). , по-существу, представляют интеграл в вероятностном пространстве с плотностью распределения случайной величины f(t)=1/T, поэтому (МО
, по-существу, представляют интеграл в вероятностном пространстве с плотностью распределения случайной величины f(t)=1/T, поэтому (МО  равно нулю))
равно нулю)) .
. совпадает с матрицей Y. Отсюда
совпадает с матрицей Y. Отсюда ,
,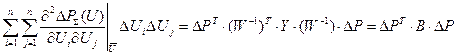 ,
,
 - так называемая матрица квадратичных коэффициентов потерь энергии.
- так называемая матрица квадратичных коэффициентов потерь энергии. . Тогда
. Тогда 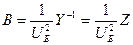 . Отсюда следует вполне приемлемое для практических расчетов выражение
. Отсюда следует вполне приемлемое для практических расчетов выражение ,
,
 - потери мощности, соответствующие режиму математических ожиданий нагрузок; Т - временной интервал определения потерь энергии (Т=24ч.);
- потери мощности, соответствующие режиму математических ожиданий нагрузок; Т - временной интервал определения потерь энергии (Т=24ч.);  - элементы матриц сопротивлений и корреляционных моментов мощности. Здесь уместно заметить, что знак элементов матрицы корреляционных моментов не зависит от направления мощности в узлах. Однако при изменении принятого за положительное направления мощности знаки элементов матрицы Y, а следовательно, и Z=Y-1 меняются на противоположные. В общепринятом представлении матрицы Y (нагрузка положительна) диагональные элементы отрицательны. Отрицательны также и элементы матрицы Z. Однако вторая составляющая потерь положительна. Это следует учесть при определении потерь.
- элементы матриц сопротивлений и корреляционных моментов мощности. Здесь уместно заметить, что знак элементов матрицы корреляционных моментов не зависит от направления мощности в узлах. Однако при изменении принятого за положительное направления мощности знаки элементов матрицы Y, а следовательно, и Z=Y-1 меняются на противоположные. В общепринятом представлении матрицы Y (нагрузка положительна) диагональные элементы отрицательны. Отрицательны также и элементы матрицы Z. Однако вторая составляющая потерь положительна. Это следует учесть при определении потерь. , исходящего из базисного узла, и суммы математических ожиданий мощностей нагрузок в электрической сети. Эти потери вычисляются в ячейке G29. Вторая составляющая потерь определяется в ячейке G30, где записана формула =-СУММПРОИЗВ(E18:G20;F3:H5)/$A$27^2/2 (ссылки см. табл. 3.16), соответствующая математическому выражению
, исходящего из базисного узла, и суммы математических ожиданий мощностей нагрузок в электрической сети. Эти потери вычисляются в ячейке G29. Вторая составляющая потерь определяется в ячейке G30, где записана формула =-СУММПРОИЗВ(E18:G20;F3:H5)/$A$27^2/2 (ссылки см. табл. 3.16), соответствующая математическому выражению .
.


