Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение инженерных задач на ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проектирование ЭТ Для решения прикладных задачи с помощью ЭТ следует разработать проект - определить необходимую совокупность таблиц, диаграмм, сгруппировать их по тематике на отдельных листах, определить, какие блоки таблиц отводятся под исходные, промежуточные и результирующие данные, выбрать математические средства (функции, процедуры, инструментальные средства Excel и др.) обработки данных. Для этого рекомендуется четко придерживаться стандартной схемы программирования: · Математическая постановка задачи; · Математический алгоритм; · Программный алгоритм; · Заполнение таблиц; · Отладка таблиц; · Документация. В математической постановке и при выборе алгоритма решения задачи следует учитывать табличную направленность Excel, максимально использовать набор встроенных функций и процедур. На данном этапе актуальна проблема последовательности формирования таблиц - поэтапного перехода от исходной информации к результирующим данным. В отличие от систем управления базами данных (СУБД), например Access, в Excel нет удобных средств автоматического контроля данных - для контроля правильности заполнения таблиц предлагается либо заполнять их через меню Данные/Формы, либо выполнять фильтрацию по критерию (Данные/ Фильтр), либо предусматривать столбцы (строки) - индикаторы контроля, где с помощью функции Если() осуществляется построение критерия правильности данных. При отладке таблиц следует быть особенно изобретательными на предмет - что бы мне еще придумать, чтобы получить явно неверное решение. Этап разработки документации, по мнению любого программиста, - самый неприятный - дополнительная работа, безусловно необходимый (через неделю мы позабудем детали, а через месяц – все), а потому самый ответственный. Excel - достаточно удобный для документации программный продукт - без всяких проблем здесь можно написать целую книгу с вашими гениальными мыслями. Основные функции Суммирование Наиболее часто в приложениях Excel применяются функции суммирования, определения среднего, максимального или минимального значения массива данных (табл. 3.1)
Таблица 3.1
Замечания
1. Допускаются ссылка на ячейку или блок, текстовое представление числа, дата, логические значения. 2. Пустые ячейки игнорируются. Тексты или значения ошибок в массивах данных приводят к ошибкам. 3. Для суммирования чисел в строке или столбце при записи результата в соседних ячейках в Excel имеется кнопка “S“ автосуммирования. 4. Аргументы функций СУММПРОИЗ, СУММРАЗНКВ, СУММСУММКВ, СУММКВРАЗН, которые оперируют с составными массивами, должны иметь одинаковые размерности. Если это не так, то функция возвращает значение ошибки #ЗНАЧ!. 5. Аргументы функций СУММРАЗНКВ(),СУММКВРАЗН(),содержащие тексты, логические значения или пустые ячейки, игнорируются. 6. Функция СУММСУММКВ(), как правило, используется в статистических вычислениях. Примеры Функция СУММ() СУММ("3"; 2; ИСТИНА) равняется 6, так как текстовые константы преобразуются в числа, а логическое значение ИСТИНА преобразуется в число 1. Если ячейка A1 содержит "3", а ячейка B1 содержит ИСТИНА, то: СУММ(A1; 2; B1) равняется 2, так как нечисловые значения в ссылке не преобразуются. СУММ(А1:С1;D3:E3) – суммирование содержимого двух блоков чисел. Функции МАКС(), МИН() Если ячейки A1:A5 содержат числа 10, 7, 9, 27 и 2, то: МАКС(A1:A5) равняется 27, МИН(A1:A5) равняется 2, МИН(A1:A5; 0) равняется 0. Функция СРЗНАЧ() Если ячейки A1:A5 имеют имя "Баллы" и содержат числа 10; 3; 0; 0 и 2, то СРЗНАЧ(A1:A5) равняется 3 (15/5). СРЗНАЧ(Баллы) также равняется 3; СРЗНАЧ(A1:A5; 9) равняется 4. Функция СУММПРОИЗВ () СУММПРОИЗВ({3;4:8;6}; {2;7:6;7}) (точка с запятой отделяет два элемента одной и той же строки, а двоеточие переводит на новую строку) перемножает все компоненты двух массивов, а затем складывает полученные произведения, 3·2 + 4·7+ + 8·6 + 6·7, в результате чего будет возвращено число 124.
Замечания · Функция СУММПРОИЗВ() может быть использована для получения скалярного произведения двух векторов. · Если в приведенном примере числа хранятся в ячейках A1:B2 и D1:E2, то рассматриваемая функция возвращает тот же самый результат, что и формула СУММ(A1:B2* D1:E2), введенная как массив. Здесь в качестве параметра функции СУММ() фигурирует массив - результат операций с двумя массивами. Такой подход дает более общее средство для выполнения действий, подобных функции СУММПРОИЗВ(), например для вычисления суммы квадратов элементов в массиве A1:B3 - СУММ(A1:B3^2). Функции СУММКВ(), СУММРАЗНКВ(), СУММСУММКВ(), СУММКВРАЗН() СУММКВ (3; 4) равняется 25 СУММРАЗНКВ ({2; 3; 9; 1; 8;}; {6; 5; 11; 7; 5}) равняется -97 СУММСУММКВ ({2; 3; 9; 1; 8; 7; 5}; {6; 5; 11; 7; 5; 4; 4}) равняется 521 СУММКВРАЗН ({2; 3; 9; 1; 8; 7; 5}; {6; 5; 11; 7; 5; 4; 4}) равняется 79 Замечание. Последняя функция, как и функция СУММКВ(), может быть использована для получения минимизируемой суммы квадратов невязок токов или мощностей в узлах электрической сети. Функция СУММЕСЛИ(интервал; критерий; с-интервал) суммирует ячейки, специфицированные заданным критерием. Параметры. В параметрах представлены два блока чисел – те, что участвуют в критерии (интервал) и те, что условно суммируются (с-интервал). Критерий задается в форме числа, выражения или текста. Например, 32, ">32", "яблоки". Согласно критерию текущее число суммируется, если соответствующее число из интервала удовлетворяет критерию. С-интервал - это ячейки для суммирования. Ячейки в с-интервале суммируются, только если соответствующие им ячейки в аргументе "интервал" удовлетворяют заданному критерию. Если параметр «с-интервал» опущен, то суммируются ячейки в аргументе «интервал». Пример Пусть ячейки B1:B4 содержат следующие величины стоимости электрических аппаратов: 100, 200, 300 и 400 тыс. руб. для напряжений 10, 35, 35, 110 кВ (блок A1:A4). Стоимость аппаратов напряжением выше 10 кВ выражается функцией СУММЕСЛИ(A1:A4;">10";B1:B4) и равна 900 тыс. руб, так как первое напряжение не удовлетворяет критерию отбора.
Функция СЧЁТ(Арг1; Арг2;...) используется для получения количества числовых ячеек в блоках данных. Тексты или индикация об ошибках игнорируются. Примеры ( рис. 3.1 ) СЧЁТ(A6:A7) равняется 2. СЧЁТ(A4:A7) равняется 3 (Дата – это число, пустая ячейка игнорируется). СЧЁТ(A2; A6:A9; "Двенадцать"; 5) равняется 3 (ошибка игнорируется). СЧЁТ(A1:A9;;"2"), где параметр "2" является текстовым изображением числа, равняется 5 (пробел-параметр рассматривается как число). СЧЁТ(0,1; ИСТИНА; "три"; 4;; 6,6666; 700;; 9; #ДЕЛ/0!) равняется 8. Функции даты Excel для Windows использует систему дат, в которой дата представляется числом в интервале от 1 до 65380, соответствующем дате в интервале от 1 января 1900 года до 31 декабря 2078 года. Дата представляется числом дней с начала ХХ века (1900 г.). В ячейке дата может быть представлена различными форматами, например ДД.ММ.ГГ; ММ.ГГ. В числовом формате даты цифры справа от «десятичной» запятой представляют время; цифры слева от «десятичной» запятой представляют дату. Например, дата в числовом формате 367,5 представляет код даты и времени, соответствующий 12 часам дня 2 января 1901 года.
Функция СЕГОДНЯ() в озвращает текущую дату в числовом формате. Функция ГОД(дата) возвращает год, соответствующий аргументу "дата" в числовом формате. Год определяется как целое в интервале 1900-2078. Можно задать аргумент "дата" как текст, например как "19 Мар 1955" или "19.3.55", а не как число. Текст автоматически преобразуется в дату в числовом формате. Примеры. ГОД("5.7.90") равняется 1990. ГОД(29747,007) равняется 1981. Функция МЕСЯЦ(дата) возвращает месяц, соответствующий аргументу "дата" в числовом формате. Месяц определяется как целое в интервале от 1 (Январь) до 12 (Декабрь). Примеры. МЕСЯЦ(366) равен 12. МЕСЯЦ(367) равен 1. Функция ТДАТА() возвращает текущую дату и время в числовом формате. Функция меняет свое значение только при перевычислении рабочего листа или при выполнении макроса, содержащего эту функцию. Значение этой функции не обновляется непрерывно. Примеры Если встроенные часы компьютера установлены на 12:30:00 1 января 1987 года, то: ТДАТА() равняется 31778,52083. Десять минут спустя: ТДАТА() равняется 31778,52778. Формульные расчеты Тип оборудования Показательным для электроэнергетиков примером применимости функции СУММЕСЛИ(), является задача определения количества или иных показателей того или иного типа оборудования, например, в ячейке С8 (рис. 3.2) записана формула =СУММЕСЛИ(A2:A6;"ВМП";C2:C6). Самостоятельная работа · На новом листе «Выключатель» повторите расчеты, представленные на рис. 3.2. · Определите суммарное число выключателей МГГ. · Выделите одну ячейку (например, F2) для указания необходимого типа выключателя (в Е2 текст «Тип»). Исправьте формулы в В8, С8 так, чтобы они ссылались на ячейку F2, где указан тип выключателя. · Добавьте еще один тип выключателя (ВМТ) и попытайтесь получить таблицу результатов по всем типам методом Данные/Таблица подстановки. · Выполните итоговое суммирование выключателей методом Данные/Итоги. Несомненно, последняя процедура вам понравилась более всего, но рассматриваемая функция в некоторых приложениях позволяет получить достаточно красивое табличное решение. · ·
Падение напряжения Задача. Известно активное R и реактивное X сопротивления линии электропередач (ЛЭП), напряжение U1 и поток мощности S 1 =P 1 +jQ 1 в начале ЛЭП. Требуется вычислить продольную и поперечную составляющие падения напряжения в электропередаче, модуль напряжения V 2 в конце ЛЭП а также потери мощности и мощность S 2 =P 2 +jQ 2 в конце ЛЭП.
Расчет выполняется по формулам:
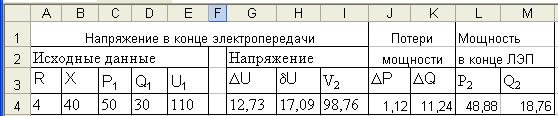
Прежде всего необходимо разработать макет таблицы расчетов, выбрать ячейки, где будут храниться исходные и результирующие данные. Для образца предлагается таблица на рис. 3.3.
Рис. 3.3 Параметры режима ЛЭП В ячейках G3:I3 записываются формулы, реализующие (3.1). Приводим их для образца G3:= (C3*A3+D3*B3)/E3; H3:= (C3*B3-D3*A3)/E3; I3:=КОРЕНЬ((E3-G3)^2+I3^2). Не пытайтесь формулы срисовать (вполне возможно, что вы, из чувства протеста, расположили таблицу в другом месте, и тогда неизбежна ошибка), постарайтесь построить их, глядя на математические формулы (3.1). Запишите формулы для расчета остальных искомых величин. Ячейкам могут быть присвоены имена. Формулы станут более понятными. При этом следует помнить, что имя ячейки (блока) должно отличаться от принятого буквенно-цифрового идентификатораячейки, например U1. Изменяя исходные данные в блоке исходных данных А3:E3, в ячейках G3:I3 будем сразу же получать результаты расчетов, что намного веселее, чем делать это с помощью калькулятора.
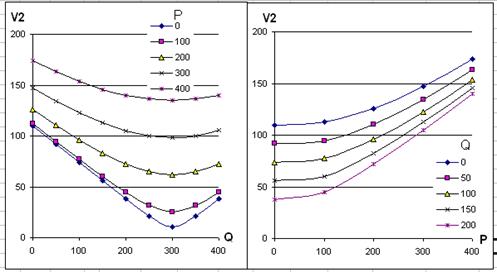
Рис. 3.4. Напряжение в конце ЛЭП Самостоятельная работа Задана электропередача с параметрами X =40 Ом; R =4 Ом; P 1=100 МВт, напряжение в начале U 1= 110 кВ. · Определить угол d между векторами напряжений. · Построить графики функций V 2(Q 1), при нескольких (4-6) значениях P 1=const (в диапазоне (0-400) МВт) и варьировании Q 1 в диапазоне (0-400) МВАр и V 2(Р 1), при нескольких значениях Q 1=const (использовать аппарат таблиц подстановок). Графики должны иметь вид, подобный рис. 3.4. · Принимая Q 1=100 МВAр, построить график функции d(P 1) при варьировании P1 в диапазоне (0-400) МВт с шагом по 50 МВт. · Объяснить причины нелинейности функций. · Построить графики функции Δ Р (Q 1) при P 1=const, Δ Р (Р 1) при Q 1=const. Можно ли считать потери мощности пропорциональными передаваемой мощности? · Пусть потери мощности Δ Р оплачивает предприятие, которое получает прибыль, пропорциональную потребляемой мощности. Суммарный доход предприятия условно можно считать пропорциональным функции Д=α Р 2-Δ Р. Построить график функции Д(P 1), при варьировании P 1= Р 2+Δ Р в диапазоне (0-300) МВт и α=0,1; 0,15; 0,2. Какие выводы можно сделать?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.30.161 (0.013 с.) |

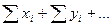

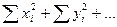
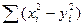
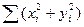





 ;
;