
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Предмет статистики, ее задачи и организацияСодержание книги
Поиск на нашем сайте
СТАТИСТИКА ЧАСТЬ I
Курс лекций для студентов сельскохозяйственных высших учебных заведений экономических специальностей
Гродно 2011 УДК 311: 330.101.541 (075.8) ББК 65. 051 Я73 С 78
Авторы: доцент, кандидат экономических наук Л.Н. Кривенкова-Леванова, старший преподаватель С.В. Грудько.
Рецензенты: кандидат экономических наук, доцент В.И. Сильванович; кандидат экономических наук, доцент М.В. Пестис.
Статистика. Курс лекций. Ч.Ι. / Л.Н. Кривенкова-Леванова, С78 С.В. Грудько. – Гродно: ГГАУ, 2011 – 156 с.
Курс лекций предназначен для подготовки студентов бухгалтерских и экономических специальностей к предмету «Статистика». Рассмотрены основные понятия, задачи и методы статистики: наблюдение, средние величины и показатели вариации, группировка, корреляционно-регрессионный анализ, ряды динамики и индексный метод.
УДК 311: 330.101.541 (075.8) ББК 65. 051 Я73
Рекомендовано межфакультетской учебно-методической комиссией экономического факультета и факультета бухгалтерского учета УО «ГГАУ» (Протокол № 6 от 13.02.2009 г.).
© Л.Н. Кривенкова-Леванова, С.В. Грудько, 2011 © УО «ГГАУ», 2011 ОГЛАВЛЕНИЕ
Тема 1. Предмет статистики, ее задачи и организация…………………………………………………………... 4 Тема 2. Статистическое наблюдение…………………….10 Тема 3 Средние величины и показатели вариации……..20 Тема 4. Группировка……………………………………...35 Тема 5. Выборочное наблюдение………………………...55 Тема 6. Корреляционно-регрессионный анализ…………70 Тема 7.Ряды динамики………………………………..….100 Тема 8. Индексный метод …………………………...…..126
Тема 1. Предмет статистики, ее задачи и организация
1. Предмет и метод статистики. 2. Основные принципы статистики. 3. Задачи статистики. Связь статистики с общественно-эконо-мическими науками. 4. Организация статистической службы в РБ. 5. Закон РБ о государственной статистике. 6. Основные понятия статистики.
ЛИТЕРАТУРА
1. Громыко Г.А. Общая теория статистики: Практикум. – М.: ИНФРА – М, 1999. –139 с. 2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: М.: Финансы и статистика, 1998. 3. Ефимова М.Р., Петрова В.В. Общая теория статистики. Учебник. – 2-е издание, – М.: ИНФРА – М. 2002, – 413 с.
4. Едронова В.С. Общая теория статистики: Учебник / – М.: Юристъ, 2001, – 511 с. 5. Статистика: Учебник / Ред. И.И. Елисеева. – М.: Проспект, 2002. – 448 с.
В 1. Предмет и метод статистики. Статистика начинает свою историю с 4-го века до н.э. с Аристотеля, который сделал первые описательные сообщения о государствах (Спарта, Греция, Рим), об их экономической мощи. 12-17 вв. – период Возрождения – привел к появлению числовой информации о рождаемости, смертности, бракосочетаниях, налогах (уже тогда появились акцизные налоги). Информация бралась из податных книг. Были установлены первые статистические закономерности: на 100 родившихся девочек рождалось 105-106 мальчиков; на 10 человек умерших приходилось 13 рожденных. Statistica (термин был введен Готфридом Ахенвалем (1719-1772)) – «сумма знаний, нужных купцам, политикам, военным, всем культурным людям». Зарождение статистики связано с зарождением учета, в частности бухгалтерского учета. Следует отличать понятие statistica от понятия statista. В 17 веке статистами называли людей, искушенных в политике. Существует около 50 определений статистики, например, одно из них приведено ниже. Статистика – это наука о количественных и качественных характеристиках жизнедеятельности человека, их изменениях, взаимосвязях и методах анализа. Предметом статистики является любой вид деятельности человека, который требует числового учета, учета качественных показателей, их систематизации и анализа, с последующим прогнозом на перспективу. Методы статистики: 1. Диалектический метод. Рассматривает явление в пространстве, времени и связях. 2. Монографический (описательный). Как правило, применяется для описания отдельно взятого или “уникального” явления. 3. Метод массового наблюдения. 4. Группировки и сводки. 5. Выборочный метод. 6. Метод дисперсионного анализа. 7. Корреляционно-регрессионный метод. 8. Индексный анализ и т.д. Методы очень широко комбинируются, сочетаются друг с другом. Как наука статистика может рассматриваться двумя своими составляющими: 1) как общественная наука; 2) как метод исследований и анализа.
В 2. Основные принципы статистики. К основным принципам статистики как науки относятся:
1) неразрывность количественного и качественного анализа изучаемых явлений; 2) описание объекта с помощью обобщающих величин; 3) аналитичность изучения явлений, т.е. раскрытие типов совокупностей, их динамики и взаимодействия.
В соответствии с законом РБ “О государственной статистике”, основными принципами организации государственной статистики являются: 1) объективность и достоверность статистической информации; 2) стабильность и сопоставимость статистических данных; 3) доступность и открытость статистической информации в пределах, установленных законодательством РБ.
В 4. Организация статистической службы в РБ. Существует два подхода к организации статистической службы: -централизованный; -децентрализованный. При централизованном способе организации статистики вся сфера деятельности статистических служб регламентируется государством. В РБ деятельность статистических органов и служб подчиняется закону "О государственной статистике в РБ", “Положением о коммерческой тайне” и двум статьям закона “О предприятии”. При децентрализованной системе организации существуют вне государственные статистические службы как при предприятиях, так и самостоятельные, которые выполняют частные заказы по сбору, обработке и анализу информации государства и различных предприятий. Проблемы в организации статистической работы: 1. Подготовка квалифицированных кадров. 2. Обеспечение автоматизации и механизации сбора, обработки и передачи информации снизу вверх и сверху вниз. 3. Проблема технического обеспечения статистических служб (персональные компьютеры, включенные в единую глобальную сеть, программное обеспечение, защита от вирусов и др.). 4. Унификация статистической информации с учетом общепринятой мировой системы национального счетоводства.
В 5. Закон РБ о государственной статистике. Закон РБ о государственной статистике принят Палатой представителей 29 октября 2004 года с изменениями и дополнениями от 4 января 2008 года. Закон состоит из 6 глав: 1. Общие положения. В данной главе рассматриваются основные термины и их определения; отношения, регулируемые настоящим законом; задачи и принципы статистики; законодательство о государственной статистике и международное сотрудничество в области государственной статистики. 2. Субъекты правоотношений в области государственной статистики, их права и обязанности. В данной главе приводится перечень органов государственной статистики; их права и обязанности; права и обязанности уполномоченных государственных организаций; права и обязанности респондентов. 3. Осуществление государственной статистической деятельности. Рассматривается ведение, планирование, финансовое обеспечение статистической деятельности, а также государственные статистические наблюдения. 4. Представление, распространение и использование статистических данных (информации). В данной главе рассматривается: кому представляются статистические данные, в каком виде, как используются, кем и каким образом формируется и ведется статистический регистр. 5. Ответственность за нарушение законодательства Республики Беларусь в области государственной статистики. В главе предусмотрена ответственность за нарушение порядка представления и искажение данных государственной статистической отчетности, а также за нарушения, допущенные при осуществлении государственной статистической деятельности.
6. Заключительные положения. В данной главе предусмотрены сроки вступления в силу данного нормативного акта, документы, утратившие силу.
В 6. Основные понятия статистики. Статистическая совокупность – это массовое явление, взятое в определенных пространственных и временных границах. Например, совокупность СПК Гродненской области, совокупность торговых точек г. Гродно, совокупность студентов экономического факультета УО «ГГАУ». Признаки статистических совокупностей – это свойства единиц объектов. В наших примерах единицами объектов могут служить каждое СПК, торговая точка, студент. Статистический показатель – это обобщающий сводный показатель признака. Система показателей – это совокупность показателей, связанных между собой. Показатели бывают: натуральные (штуки, килограммы, тонны, гектары и др.), условно-натуральные (лошадиные силы, эталонные гектары, условные банки, погонные метры), стоимостные (в денежных единицах), относительные. Статистическая совокупность количественно характеризуется: 1) индивидуальными значениями признака для единиц совокупности; 2) средней величиной показателя (признака) для всей совокупности или ее части; 3) величиной (силой) вариации (изменчивости). В 4. Понятие вариации. Колеблемость, многообразие, изменяемость значений величины признака совокупности называется вариацией. Развитие статистической науки шло от анализа средних величин в 19в. к исследованию изменчивости анализируемых показателей в начале 20в. Р.А.Фишер писал: «Вариация, взятая сама по себе, не была предметом изучения, и на нее смотрели разве только как на досадное обстоятельство, приводящее к снижению точности средней величины. С современной точки зрения изучение причин изменчивости любой переменной величины, начиная с урожайности пшеницы и кончая интеллектом человека, должно производится на основе измерения и анализа вариации, которая и сама по себе имеет большое значение». При экономическом анализе нас может интересовать не только и не столько обобщенный средний показатель, как поведение индивидуальных значений признака. Например, в двух соседних районах средняя урожайность зерновых составила 47 и 47,5 ц/га, в одном из районов урожайность в отдельных хозяйствах достигает 70 ц/га и может быть очень низкой – 33 ц/га, в другом районе урожайность по хозяйствам незначительно отличается от средней (около 5 ц/га). Встает вопрос о том, где более стабильное производство, выдерживается технология, обеспечено качественное управление отраслью.
Понятие вариации признака включает в себя оценку индивидуальных значений признака по сравнению со средними. В некоторых учебниках прибегают к оценке силы вариации при попарном сравнении индивидуальных признаков. Применение показателей вариации весьма разнообразно: 1) для оценки однородности совокупностей (совокупности); 2) для оценки концентрации и специализации производства; 3) для выявления аномальностей в совокупностях; 4) для сравнения вариации в различных совокупностях и их оценки.
Относительный размах
2. Относительное линейное отклонение:
3. Коэффициент вариации:
Для коэффициента вариации существует шкала оценки силы вариации: - если V<10%, то вариация показателя слабая; - если 10% £ V < 20%, то вариация показателя средняя; - если V ³ 20%, то вариация показателя сильная. Часто используют "полутона" силы вариации.
Например, V=3,1% – вариация слабая, практически отсутствует; V=9,3% – вариация слабая, ближе к средней; V=11,4% – вариация средняя, ближе к слабой; V=18,5% – вариация средняя, ближе к сильной; V=21-22% – вариация сильная, ближе к средней.
В нашем примере относительные показатели будут:
Таким образом, вариация успеваемости студентов сильная, ближе к средней. Это говорит о том, что не все студенты добросовестно относятся к изучению данной дисциплины. Рассмотрим использование коэффициентов вариации для оценки уровня концентрации отрасли и специализации районов. Используя первичную информацию по годовым отчетам хозяйств в двух районах, были рассчитаны значения показателей вариации по поголовью свиноматок, т.к. в первую очередь их число, плодовитость и многоплодие определяют объемы выращивания и откорма свиней в целом. Оценить уровень специализации и концентрации производства в двух районах, если есть следующие данные по поголовью свиноматок.
Таблица 3.5. Анализ поголовья свиноматок.
В обоих районах свиноматок содержат только в трех хозяйствах. Поголовье свиноматок на одно хозяйство в первом районе много больше, чем во втором. Выводы: концентрация и специализация свиноводства выше в первом районе, чем во втором.
Тема 4. Группировка
1. Сводка как один из этапов статистического наблюдения и исследования. 2. Группировка как составная часть сводки. 3. Виды группировок: - типологическая, - структурная, - аналитическая. 4. Виды интервалов группировок и их определение. 5. Равночастотные группировки и их использование. 6. Система группировок. Перегруппировка. 7. Использование дисперсионного анализа в группировках.
7.1 Анализ достоверности связей факторов. 7.2 Анализ тесноты связи факторов. 8. Правила оформления таблиц.
ЛИТЕРАТУРА:
1. Ефимова М.Р., Петрова В.В. Общая теория статистики. Учебник/ – 2- е издание., – М.: ИНФРА- М, 2002, – 413 с. 2. Едронова В.С. Общая теория статистики: Учебник / – М.: Юристъ, 2001, – 511 с. 3. Статистика: показатели и методы анализа: справ. пособие / Н.Н. Бондаренко, Н.С. Бузыгина, Л.И. Василевская и др.; под ред. М.М. Новикова. – Мн.: «Современная школа», 2005. 4. Экономическая статистика. 2-е изд., доп.: Учебник / Под ред. Ю.Н. Иванова. – М.:ИНФРА – М, 2001.
В данной таблице видно, что с увеличением площади землевладения, уменьшаются затраты из расчета на 1 акр на наемный труд, на удобрения и т.д. На сколько интенсивно осуществляется ведение сельского хозяйства можно увидеть из следующей таблицы.
Таблица 4.2. Влияние размеров ферм на уровень интенсивности земледелия (США, 1900 г.).
Эта группировочная таблица позволяют сделать определенные выводы о том, насколько крупные фермерские хозяйства эффективно работают.
В 3. Виды группировок Как метод статистического анализа группировка позволяет решить следующие задачи: 1)выделить социально-экономические типы, единиц совокупности; 2)изучить структуру однотипной совокупности; 3)обнаружить и изучить существующие связи и зависимости между признаками исследуемого явления. Исходя из этого, определяется три вида или типа группировок: 1) типологическая, 2) структурная, 3) аналитическая. Признак (статистический показатель), который положен в основу проведения группировки, называют группировочным признаком. Как правило, это наиболее важный технологический или экономический показатель, соответствующий целям исследования. От степени сложности изучаемого массового явления и от задач анализа группировки могут быть простыми, то есть по одному группировочному признаку и сложными или комбинационными (по двум или более группировочным признакам). Группировки, приведенные в таблицах 4.1 и 4.2, являются простыми, так как в каждой из таблиц один группировочный признак (это показатель, отраженный в первой графе). Рассмотрим все виды группировок. Типологической принято считать группировку совокупности на классы, социально-экономические типы, однородные группы. В сельском хозяйстве типологической модно считать группировку сельскохозяйственных угодий по виду их использования (пашня, сенокосы, пастбища, многолетние насаждения) или группировку сельскохозяйственных животных по половозрастным группам. Рассмотрим типологическую группировку студентов по полу и анализ успеваемости по различным дисциплинам Таблица 4.3). В данном примере группировка студентов проведена по признаку, который не имеет числового значения, причем пол студента рассматривается как факторный признак, а успеваемость – как результативный. По результатам группировки можно сказать, что в данной группе студентов девушки более добросовестно относятся к учебе, но юноши превосходят их в точных науках (высшей математике, информатике и программировании).
Таблица 4.3.Успеваемость студентов экономического факультета.
Но выбор типа не так прост, как кажется на первый взгляд. Например, как произвести группировку продукции по сортам? Здесь надо учитывать много показателей и государственные стандарты на их величину. Поэтому в типологических группировках группировочные признаки делят на атрибутивные и количественные. Если группировочный признак атрибутивный (сорт, порода, форма собственности, и др.), то единица совокупности или обладает этим признаком или нет. Если группировочный признак числовой, то возникают проблемы: 1) как определить число групп (интервалов), 2) какие должны быть границы группировочного признака. Поэтому придерживаются следующих правил: 1) Число интервалов при типологической группировке должно соответствовать числу предварительно намеченных частных совокупностей; 2) Границы интервалов подбирают и устанавливают таким образом, чтобы переход через них означал переход к иному типу или в новое качество. В таких группировках группировочный признак может быть факторным, а показатели, характеризующие группы единиц, могут быть результативными, т.е. можно установить некоторые зависимости между показателями. Например, группировка коров по их классности (элита-рекорд, элита, 1 класс и т.д.) позволяет установить зависимость продуктивности коров и других важных характеристик дойного стада от классности животных. Также примером такой группировки может служить группировка продукции по ее качеству или сортам. Государственными стандартами на сельскохозяйственную продукцию предусмотрены параметры по очень многим показателям, отражающим чистоту продукции от химических элементов, которые могут в последствии принести вред здоровью человека. Так, качество молока оценивается по его жирности, по содержанию белка, по микробиологической чистоте и др. Следующий вид группировки – это структурная группировка. Группировка, расчленяющая однородную совокупность единиц по долям признака, выраженного в процентах, называется структурной или вариационной. Примером может служить группировка работников по стажу работы (таблица 4.4).
Таблица 4.4. Группировка рабочих по стажу работы
Для построения такой группировки необходимо знать численность рабочих каждого интервала по стажу работы. Анализ таблицы позволяет сделать вывод о том, что на предприятии увеличились доли работников с небольшим стажем и людей предпенсионного и пенсионного возраста, что для предприятия не может считаться положительной динамикой, так как производительность труда этих групп работников всегда минимальна. Эта группировка является неполной, так как здесь отсутствуют другие показатели, отражающие качество работы, производительность труда, оплату труда и т.д. В аналитической группировке группировочный признак Хi может принимать любое числовое значение на каком-то промежутке от Хmin до Xmax. Группировочный признак выбирается с учетом цели и задач исследования. Аналитическая группировка в качестве группировочного признака всегда использует числовой показатель и позволяет установить связи и зависимости между явлениями и признаками. В аналитической группировке, также как и в других видах группировок, выделяют два вида признаков: 1) факторные, 2) результативные. Факторным является тот признак, который оказывает влияние на изменение других показателей. Результативные признаки сами изменяются под влиянием факторных. Чаще всего в аналитической группировке в качестве группировочного показателя выбирают факторный признак. Однако это необязательно. В аналитической группировке устанавливается: 1) наличие связей между показателями, 2) достоверность установленных связей, 3) направление связи (прямая или обратная), 4) теснота связи. Примечание. Независимо от вида группировки в каждой из них должны быть указаны: 1) количество единиц совокупности в каждой группе, 2) группировочный признак, и если он числовой, то его интервал и среднее значение для каждой группы, 3) система технолого-экономических показателей, характеризующих каждую группу совокупности и отражающих связи признаков, 4) итоговые строки и (или) графы. Группировка должна быть оформлена в виде таблицы с учетом всех требований ГОСТа (см. вопрос 8).
Различают Повторный и Задача 1. Для определения средней урожайности картофеля в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25.
Таблица 5.3. Результаты обследования по районам.
Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность картофеля по области. Решение. Из условия задачи выпишем значения имеющихся показателей: n=5; N=25; P=0,954; по таблицам найдем значение t=2,00. Надо определить предельную ошибку выборки Δx -? Чтобы произвести необходимые расчеты ошибки выборки, надо вычислить среднее значение урожайности картофеля и величину дисперсии.
Таблица 5.4. Расчет дисперсии
Теперь можно вычислить величину предельной ошибки урожайности:
Средняя урожайность картофеля в области (в генеральной совокупности) составит
или результат можно представить в интервальном виде 272,66ц/га Задача 2. Рассмотрим постановку и решение задач на использование механического бесповторного отбора. Используя исходную информацию по группировке покупателей можно решить несколько задач. В нашем случае они указаны по пунктам 1-3. Условие: При опросе покупателей на рынке отбирается каждый десятый покупатель со стоимостью покупки до 35 тыс. руб. и каждый десятый со стоимостью выше 35 тыс. руб. Покупатели распределились по выборке следующим образом:
Таблица 5.5. Распределение покупателей на рынке.
Определить: 1) Каковы возможные пределы ошибки выборочной средней (т.е. средней цены покупки), если ее надо гарантировать с вероятностью Р=0,954. 2) Какова вероятность того, что предельная ошибка выборочной средней стоимости покупок на 1 покупателя не превысит 1,6 тыс. руб., а предельная ошибка частости покупателей, приобретших товаров на сумму более 60 тыс. руб., не превысит 0,04 при объеме выборки n=400, если по предыдущим обследованиям известно, что доля таких покупок равна ω=0,2. 3) Каким должен быть объем выборки для того, чтобы можно было гарантировать с вероятностью p=0.954, что пределы возможной средней ошибки выборки (средней цены покупки) не превзойдут 1,6 тыс. руб., а возможной ошибки доли (частости) не превзойдут 0,04, если по предыдущим обследованиям известно, что ω=0,2.
Решение. Для решения всех трех задач необходимо найти среднюю общую стоимость одной покупки и общую дисперсию:
Средняя из частных внутригрупповых дисперсий
1) Для расчета величины ошибки используем формулу предельной ошибки средней выборочной и подставим в нее все необходимые значения.
t=2 при Р=0,954 (из таблицы) N=4000, т.к. осуществлен десятипроцентный отбор и n=400 Вывод: средняя цена покупки в генеральной совокупности будет Хген=36 ± 0,78 тыс. руб. 2) В пункте 2 необходимо произвести расчеты по величине вероятности для цены покупки и для доли покупателей, поэтому из формул ошибок средней и доли необходимо вычислить величину коэффициента доверия t, а затем по таблицам найти значение вероятностей. а) б)
Вывод: Вероятность средней цены покупки велика (0,99), а вероятность доли покупателей практически равна нулю. 3) В третьем пункте предлагается рассчитать объемы выборки для очередного выборочного наблюдения. Для этого мы выбираем формулу из таблицы 5.2. и подставляем в нее все необходимые числовые значения. а) t=2 (из таблиц), Dx=1,6 б) Dw=0,04, w=0,2 Вывод: Для оценки средней цены покупки надо опросить 105 человек, а для оценки доли покупателей необходимо побеседовать с 200 покупателями.
..
Рисунок 6.3. Точечная диаграмма связи показателей
Это достигается при использовании метода наименьших квадратов (МНК), разработанного К.Ф.Гауссом (1777–1855). Для прямой линии Получим:
В учебниках по общей теории статистики, как правило, даются формулы для расчета параметров уравнения регрессии
Эти формулы получены при использовании правила определителей второго порядка для решения систем двух линейных уравнений с двумя неизвестными, где в знаменателе стоит значение главного определителя:
где Δ – главный определитель системы. В числителях формул 6.4 и 6.5 стоят определители, где в главном определителе заменен один из столбцов на столбец свободных членов. В полученном уравнении регрессии параметры носят следующие названия: а0 – свободный член; а1 – коэффициент регрессии. В уравнении свободный член может иметь экономико-технологический смысл, а может не иметь. Например, если уравнение отражает уровень продуктивности животных в зависимости от уровня кормления, то свободный член должен показывать уровень продуктивности животных при «нулевом» кормлении, что является абсурдным. С точки зрения математики свободный член отражает значение точки пересечения прямой линии с осью ординат. Корреляционно-регрессионная связи существует только в определенной области (в области размаха вариации для Х и У) Парный коэффициент регрессии всегда интерпретируем. Парный коэффициент регрессии показывает, на сколько единиц своего измерения в среднем изменится результат (У), если факторный показатель (Х) изменится в среднем на единицу своего измерения. Например, получено уравнение зависимости уровня рентабельности от уровня механизации производственного процесса: Ỹх = 10 + 0,301Х, где значения обоих параметров уравнения имеют смысл: а0=10% будет отражать уровень рентабельности при полном отсутствии механизации труда; а1=0,301% показывает, что уровень рентабельности увеличится на 0,3%, если уровень механизации вырастет на 1%. Имея значения параметров уравнения регрессии, вычисляют теоретические значения результативного показателя, подставляя в уравнение фактические значения Хi (см. таблицу 6.2), для дальнейшей работы с моделью.
В 15. Рекомендации по составлению различных корреляционно-регрессионных моделей. Все виды моделей можно классифицировать следующим образом: 1) Объемные или количественные модели. Это такие модели, где и результативный признак и факторы, на него влияющие, являются объемными или количественными показателями. К таким моделям можно отнести зависимость выхода продукции от наличия (объема) различных ресурсов. 2) Интенсивные модели. В них все показателя являются качественными или интенсивными. Например, зависимость уровня себестоимости единицы продукции растениеводства от удельных затрат труда на 1га, от урожайности, от стоимости 1 тонны удобрений NPK действующего вещества и т.д. 3) Третий вид моделей – смешанный, где результативным показателем выступает объемный признак, а среди факторов могут быть как объемные, так и интенсивные или качественные признаки. Здесь главное выдержать наличие технико-экономи-ческой связи показателей, включенных в модель. Однако существуют рекомендации, чего нельзя допускать в многофакторных корреляционно-регрессионных моделях. 1) Нельзя допускать включение в модель факторов, которые сами зависят от результативного показателя. Например, в
модель себестоимости продукции нельзя включать уровень рентабельности, т.к. он сам зависит от себестоимости. 2) Признаки-факторы не должны быть составными частями результативного показателя. Например, нельзя строить модель зависимости уровня себестоимости от составляющих ее статей или элементов затрат. 3) Как уже говорилось в вопросе 1, нельзя включать в модель факторы, которые относительно друг друга являются мультиколлинеарными. 4) Нельзя в модель интенсивного типа включать объемные факторы. Например, размер посевной площади никак не может влиять на урожайность.
Тема 7. Ряды динамики
1. Понятие о динамических рядах. Виды рядов динамики. 2. Показатели ряда динамики. 3. Приемы выравнивания рядов динамики. 4. Тренд. Аналитическое выравнивание ряда. Прогнозы по тренду. 5. Сезонные колебания в рядах динамики. 6. Модели рядов с учетом тенденции и сезонности. 7. Корреляция рядов динамики. Регрессия рядов динамики. 8. Понятия интерполяции и экстраполяции в рядах динамики.
ЛИТЕРАТУРА:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: М.: Финансы и статистика, 1998. 2. Ефимова М.Р., Петрова В.В. Общая теория статистики. Учебник/ – 2- е издание., – М.: ИНФРА- М, 2002, – 413 с. 3. Едронова В. С. Общая теория статистики: Учебник / – М.: Юристъ, 2001, – 511 с 4. Кривенкова Л.Н. Статистические методы анализа и моделирования свиноводства (на уровнях отдельного предприятия и региона). Диссертация на соискание ученой степени к.э.н. С.Петербург, 1992, – 149с. 5. Плошко Б.Г., Елисеева И.И. История статистики: Учеб.пособие / – М.: Финансы и статистика, 1990, – 295с. 6. Статистика: показатели и методы анализа: справ. пособие/ Под ред. М.М. Новикова. – Мн.: “Современная школа”, 2005.– 268 с. 7. Сельское хозяйство РБ: статистический сборник / ред.кол.: В.С. Метекс; В.Н. Синкевич; Л.Л. Выбчик и др.; Министерс |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.248.140 (0.015 с.) |

 (3.24)
(3.24) (3.25)
(3.25)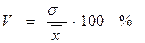 (3.26)
(3.26)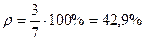


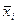
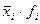
 280 ц/га.
280 ц/га.
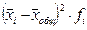
 ц/га.
ц/га. ц/га
ц/га ц/га
ц/га 287,34ц/га
287,34ц/га )
)
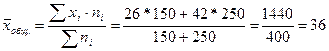 тыс. руб.
тыс. руб.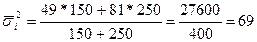
 тыс. руб.
тыс. руб. ; P(4,06)=0.99;
; P(4,06)=0.99; 
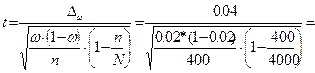 0,006
0,006  P(0,0066)=0,008
P(0,0066)=0,008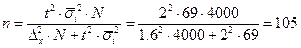

 x
x составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными).
составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными).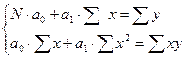 (6.3)
(6.3)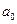 и
и 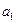 :
: (6.4)
(6.4)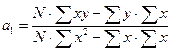 (6.5)
(6.5) (6.6)
(6.6)


