
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 7. Использование дисперсионного анализа в группировках.Содержание книги
Поиск на нашем сайте
В результате проведения анализа показателей, включенных в группировку, можно установить наличие связей межу ними. Однако наши выводы о наличии связей могут оказаться ошибочными. Поэтому установленные связи должны быть подтверждены с помощью критериев достоверности или другими статистическими методами. Если группировочный признак является факторным, а остальные показатели, включенные в анализ – результативные признаки, то достоверность зависимости результатов от фактора можно доказать с помощью критерия Фишера. В экономическом анализе принято предполагаемое утверждение называть рабочей гипотезой. В противовес рабочей гипотезе о наличии связей между признаками может быть установлена "ноль-гипотеза", утверждающая отсутствие достоверных связей между анализируемыми показателями.
Немецкий статистик и экономист Вильгельм Лексис (1837–1914) вывел широко известное правило сложения дисперсий, которое было центральным местом в теории устойчивости (теории дисперсий). В предыдущих темах мы уже рассмотрели показатели вариации, особое место среди которых занимает дисперсия. Но вариация результативного показателя обычно обусловлена многими факторами, которые могут быть разделены на две большие группы: систематические и случайные. И очень важно уметь из общего объёма влияния выделить вариацию за счёт постоянно действующих факторов. Из темы "Показатели вариации" мы знаем, как определить общую дисперсию признака, отражающую объем вариации показателя независимо от факторов на него влияющих. Используем ту же систему обозначений, что и в теме "Средние величины и показатели вариации".
где Хi – значение анализируемого показателя у каждой единицы объекта,
f– частота значений анализируемого показателя. Дисперсия, отражающая вариацию результата под воздействием конкретного фактора, называется межгрупповой или факторной. Ее вычисляют по формуле:
где Однако на результативный показатель влияет не только группировочный фактор, рассматриваемый в анализе, но и другие факторы. Кроме того, всегда присутствует случайная колеблемость анализируемого показателя. Сила случайной (остаточной) колеблемости оценивается по величине остаточной дисперсии, которую можно вычислить двумя способами. При первом – используем правило сложения дисперсий, которое рассматривается в курсе математической статистики:
Из нее получаем формулу для расчета остаточной дисперсии:
Однако такая последовательность расчетов дисперсий не позволяет выявить ошибки расчетов. Поэтому лучше остаточную дисперсию вычислить по формуле средней взвешенной из внутригрупповых дисперсий, а затем проверить правильность расчетов по формуле сложения дисперсий.
На базе полученных дисперсий вычисляют значение F–критерия (критерия Фишера) по одной из формул:
Символом "ν" обозначается "число степеней свободы". В группировке число степеней свободы определим по формулам:
νм.г. = m – 1, (4.9) где m – число групп
νост. = n – m, (4.10) где n – объём изучаемой совокупности В учебниках по теории статистики для обозначения числа степеней свободы часто используют следующие символы:
Отношение
F-критерий можно рассчитать, используя значение такого показателя тесноты связи, как индекс детерминации (см. ниже по тексту):
Расчетное значение F-критерия необходимо сравнить с табличным значением критерия Фишера. Табличное значение F-критерия находим по таблицам Фишера, определив столбец по значению νм.г. и строку по νост. Если Fрасчетное > Fтабл., то подтверждается рабочая гипотеза о наличии связи между показателями и опровергается "ноль-гипотеза". Если Fтабл. ≥ F расч., то подтверждается "ноль-гипотеза" и опровергается рабочая гипотеза. Если установлена достоверная связь показателей, то нужно установить тесноту связи, используя эмпирические коэффициенты корреляции и детерминации. Эмпирический коэффициент корреляции η отражает силу связи между результативным и факторным показателем. Если 0< η ≤ 0,3 – связь слабая 0,3 ‹ η ≤ 0,7 – связь средняя 0,7 ‹ η ≤ 1 – связь тесная Эмпирический коэффициент корреляции вычисляют по формуле:
(4.13)
Эмпирический коэффициент детерминации η2 показывает, какая часть вариации результативного показателя зависит от вариации факторного признака. Он может быть выражен в процентах. Рассмотрим числовой пример. Среди молодых механизаторов сельскохозяйственных предприятий есть прошедшие обучение в СПТУ (колледжах) и есть прошедшие обучение непосредственно в хозяйстве. Был проведен конкурс молодых механизаторов. В результате проведенного конкурса известна производительность труда всех молодых механизаторов и необходимо установить, зависит ли их производительность труда от формы подготовки. Для анализа составим сложную типологическую группировку по формам обучения и показателям производительности труда в каждой группе (таблица 4.9).
Расчеты по группировке.
Средние значения производительности труда в группах и в целом по совокупности найдем по формуле средней арифметической взвешенной:
Вычислим все необходимые дисперсии. Причем остаточную дисперсию рассчитаем двумя способами и проверим выполнение правила сложения дисперсий.
или
Установим достоверность зависимости производительности труда молодых механизаторов от формы подготовки, используя F-критерий, рассчитав его по формуле (4.12) с использованием имперического коэффициента детерминации.
Поскольку Fрасч. > Fтабл., можно утверждать, что производительность труда молодых механизаторов зависит от формы подготовки, т.е. "ноль-гипотеза" является несостоятельной. Эмпирические коэффициенты корреляции и детерминации показывают, что связь между анализируемыми показателями слабая (η=0,214) и вариация производительности труда только на 4,6% зависит от формы подготовки механизаторов.
В 8. Правила оформления таблиц. Статистическая таблица является наиболее компактной формой представления информации. Кроме того, в статистических исследованиях используются промежуточные расчетные таблицы, которые позволяют упростить математические вычисления или использовать электронные таблицы ПЭВМ. Виды таблиц весьма разнообразны, но ко всем предъявляются некоторые стандартные требования. 1. Если таблиц много, то они должны быть пронумерованы. 2. Каждая таблица должна иметь заголовок, отражающий ее суть. Заголовок может содержать указание на объект, время и место исследования. 3. Заголовки граф и строк должны быть краткими и не допускают сокращений, кроме общепринятых. 4. Графы и строки должны содержать единицы измерения, проставленные через запятую (например: Численность работников, чел.) 5. Округление чисел в пределах одной и той же строки или графы следует проводить с одинаковой степенью точности. 6. Отсутствие числового значения в зависимости от причины может быть отмечено следующими символами: а) "Х" – если позиция в таблице не подлежит заполнению, в) "…" или "нет свед.", или "н.св." – если отсутствуют сведения, с) "–×" при отсутствии явления. 7. Если числовое значение показателя очень мало по сравнению с другими значениями, то используют обозначения "0,0" или "0,00". 8. Таблицы должны содержать итоговые строки и графы. 9. Желательно, чтобы таблица целиком размещалась на странице. 10. Допускается расположение таблицы поперек страницы. 11. Если таблица не помещается на одной странице, то допускается перенос ее части на другую страницу с указанием на то, что это продолжение таблицы с номерами граф. 12. В тексте кроме ссылки на таблицу должен быть дан ее анализ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.185 (0.008 с.) |

 (4.3)
(4.3) – среднее значение показателя по всей совокупности,
– среднее значение показателя по всей совокупности, (4.4)
(4.4) - среднее значение показателя в каждой группе.
- среднее значение показателя в каждой группе. (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) , или
, или  , или νм.г.
, или νм.г. , или
, или  , или νост.(случ)
, или νост.(случ) называется средним квадратом и часто обозначается как
называется средним квадратом и часто обозначается как 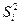 , тогда
, тогда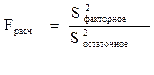 (4.11)
(4.11)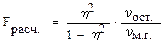 (4.12)
(4.12)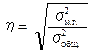
 =
= 


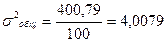







 Fрасч>Fтабл
Fрасч>Fтабл ;
; 



