
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 3. Виды парной корреляционно-регрессионной связи.Содержание книги
Поиск на нашем сайте
К самым простым корреляционно-регрессионным связям относят парные или однофакторные связи. Среди парных выделяют: линейные и криволинейные связи. Результативный показатель обозначается У, факторный признак обозначается Х. Исходную базу данных (цифровую информацию) можно представить в виде горизонтальной или вертикальной таблицы. Например,
Таблица 6.1. База данных для исследования связи показателей
В исходной информации вместо «№ по порядку» могут быть указаны наименования хозяйств (точек совокупности). Если задана информация в таком виде, то каждой паре чисел на декартовой системе координат в соответствие может быть поставлена точка. На рисунках 6.1 и 6.2 изображены некоторые виды таких графиков, которые называются точечными диаграммами. Виды парной корреляционно-регрессионной связи:
1. Линейное уравнение регрессии:
2. Степенная связь факторов:
Это уравнение может быть приведено к линейному уравнению путем логарифмирования: log Y = log a + b log х
3. Показательная связь факторов: Уравнение приводится к линейному виду через логарифмирование: log у = log a +(log b) х
4. Гиперболическая зависимость результата от фактора: Ỹх= а + Это уравнение преобразуется в линейное уравнение подстановкой величины, обратной Х, т.е. Z= тогда Ỹz = a + bz.
Рисунок 6.1. – Прямая (положительная) регрессия
Рисунок 6.2. – Обратная (отрицательная) регрессия
5. Параболическая связь:
В 4. Парная линейная корреляционно-регрессионная модель. Процесс построения корреляционно-регрессионной модели сводится к осреднению значения результата и фактора. Пусть исходные данные Х и У сведены в таблицу и дополнительно рассчитаны Х2, ХУ, Ух.
Таблица 6.2. Информация для построения уравнения регрессии
В дальнейшем, после расчета уравнения регрессии и нахождения по нему теоретических значений результативного показателя, необходимо будет проверить выполнение равенства:
Для парной связи следует построить график (точечную диаграмму), и выявить наличие ошибок информации и (или) аномальные точки: Уравнение регрессии должно быть таким, чтобы обеспечить минимум суммы квадратов отклонений эмпирических значений результативного показателя от теоретических значений, полученных по модели: ỹх
Y
... (*) – «аномальные» точки ... или ошибки ... * информации ..
Рисунок 6.3. Точечная диаграмма связи показателей
Это достигается при использовании метода наименьших квадратов (МНК), разработанного К.Ф.Гауссом (1777–1855). Для прямой линии Получим:
В учебниках по общей теории статистики, как правило, даются формулы для расчета параметров уравнения регрессии
Эти формулы получены при использовании правила определителей второго порядка для решения систем двух линейных уравнений с двумя неизвестными, где в знаменателе стоит значение главного определителя:
где Δ – главный определитель системы. В числителях формул 6.4 и 6.5 стоят определители, где в главном определителе заменен один из столбцов на столбец свободных членов. В полученном уравнении регрессии параметры носят следующие названия: а0 – свободный член; а1 – коэффициент регрессии. В уравнении свободный член может иметь экономико-технологический смысл, а может не иметь. Например, если уравнение отражает уровень продуктивности животных в зависимости от уровня кормления, то свободный член должен показывать уровень продуктивности животных при «нулевом» кормлении, что является абсурдным. С точки зрения математики свободный член отражает значение точки пересечения прямой линии с осью ординат. Корреляционно-регрессионная связи существует только в определенной области (в области размаха вариации для Х и У) Парный коэффициент регрессии всегда интерпретируем. Парный коэффициент регрессии показывает, на сколько единиц своего измерения в среднем изменится результат (У), если факторный показатель (Х) изменится в среднем на единицу своего измерения. Например, получено уравнение зависимости уровня рентабельности от уровня механизации производственного процесса: Ỹх = 10 + 0,301Х, где значения обоих параметров уравнения имеют смысл: а0=10% будет отражать уровень рентабельности при полном отсутствии механизации труда; а1=0,301% показывает, что уровень рентабельности увеличится на 0,3%, если уровень механизации вырастет на 1%. Имея значения параметров уравнения регрессии, вычисляют теоретические значения результативного показателя, подставляя в уравнение фактические значения Хi (см. таблицу 6.2), для дальнейшей работы с моделью.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.006 с.) |

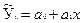
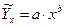 или
или 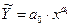
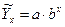
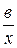
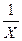






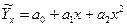
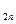
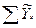
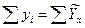
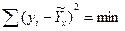 (6.2)
(6.2) * ..
* .. x
x составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными).
составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными).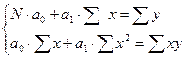 (6.3)
(6.3)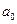 и
и 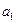 :
: (6.4)
(6.4)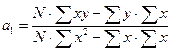 (6.5)
(6.5) (6.6)
(6.6)


