Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произведение ts называется предельной ошибкой выборки.Содержание книги
Поиск на нашем сайте
Можно доказать, что величина предельной ошибки может быть вычислена по формуле
т.е. предельная ошибка (Dх) зависит от трех факторов: s2, n и t (дисперсии, объема выборки, величины коэффициента доверия или вероятности) следующим образом: 1) величина дисперсии (s2) отражает силу вариации, поэтому чем выше сила вариации анализируемого показателя, тем больше ошибка выборки; 2) чем больше объем выборки n, тем меньше ошибка исследования; 3) чем больше вероятность Р, тем меньше ошибка. Значительно величина ошибки (Dx) зависит не только от объема выборки n, но и от доли выборки относительно генеральной совокупности. Величина значения коэффициента доверия
зависит только от того, с какой вероятностью необходимо гарантировать пределы ошибки выборки. Если известны величина дисперсии s2 и коэффициент доверия t, то из формулы (5.6) можно получить формулу для расчета объема выборки
На основании формул (5.6) и (5.8) решаются все три поставленные задачи. Для доли выборки эти формулы трансформируются:
В 5. Выбор формул для оценки результатов выборочного наблюдения при повторном и бесповторном способах отбора. Система формул (5.6-5.11) является основой для построения формул для оценки предельной ошибки выборки при различных способах и видах выборки, что отражено в следующей таблице 5.1. Необходимо помнить, что выражение, стоящее под радикалом, дает значение средней ошибки выборки. Из таблицы 5.1 видно, что при бесповторном способе отбора в формулах добавляется разность между 1 и долей выборки относительно объема генеральной совокупности (1–n/N). В таблице 5.2 отражены формулы для расчета объема выборки. Все представленные в этой таблице формулы получают из формул таблицы 5.1 путем алгебраических преобразований. Таблица 5.1. Предельная ошибка выборки для некоторых способов формирования выборочной совокупности
Их используют тогда, когда уже были ранее проведены аналогичные исследования и рассчитаны дисперсии и ошибки выборки. Тогда расчет объема выборки позволяет не делать лишнюю ненужную работу, при этом сохраняя достаточно высокую точность и надежность выборочного исследования.
Таблица 5.2. Необходимый объем выборки для некоторых способов формирования выборочной совокупности
В 6. Особенности малой выборки. В перерабатывающей промышленности и в сельском хозяйстве, где необходимо установить качество продукции используют метод оценки проб продукции в лабораторных условиях. Как правило, количество проб небольшое. В каждом конкретном случае экспериментальным способом отрабатывались методики взятия проб и оценки качества продукции. Малой выборкой считают выборку, объем которой находится в пределах от 5 до 30 единиц, т.е. 5<n£30. При малой выборке нельзя принимать равенство дисперсий Закон распределения случайных ошибок малой выборки был найден английским ученым Вильямом Госсетом (1876–1937) и опубликован в 1908 г. под псевдонимом «Стьюдент». Для малой выборки расчет предельной ошибки выборки найдем по формуле:
где Разность (n-1) называется числом степеней свободы и обозначается Стьюдентом разработаны таблицы, которыми все пользуются для определения предельного значения t, при различных значениях вероятности (Р). Современные таблицы Стьюдента, которые имеются в каждом учебнике статистики и теории вероятностей, более подробные.
Рассмотрим несколько задач по выборочному наблюдению. Задача 1. Для определения средней урожайности картофеля в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25.
Таблица 5.3. Результаты обследования по районам.
Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность картофеля по области. Решение. Из условия задачи выпишем значения имеющихся показателей: n=5; N=25; P=0,954; по таблицам найдем значение t=2,00. Надо определить предельную ошибку выборки Δx -? Чтобы произвести необходимые расчеты ошибки выборки, надо вычислить среднее значение урожайности картофеля и величину дисперсии.
Таблица 5.4. Расчет дисперсии
Теперь можно вычислить величину предельной ошибки урожайности:
Средняя урожайность картофеля в области (в генеральной совокупности) составит
или результат можно представить в интервальном виде 272,66ц/га Задача 2. Рассмотрим постановку и решение задач на использование механического бесповторного отбора. Используя исходную информацию по группировке покупателей можно решить несколько задач. В нашем случае они указаны по пунктам 1-3. Условие: При опросе покупателей на рынке отбирается каждый десятый покупатель со стоимостью покупки до 35 тыс. руб. и каждый десятый со стоимостью выше 35 тыс. руб. Покупатели распределились по выборке следующим образом:
Таблица 5.5. Распределение покупателей на рынке.
Определить: 1) Каковы возможные пределы ошибки выборочной средней (т.е. средней цены покупки), если ее надо гарантировать с вероятностью Р=0,954. 2) Какова вероятность того, что предельная ошибка выборочной средней стоимости покупок на 1 покупателя не превысит 1,6 тыс. руб., а предельная ошибка частости покупателей, приобретших товаров на сумму более 60 тыс. руб., не превысит 0,04 при объеме выборки n=400, если по предыдущим обследованиям известно, что доля таких покупок равна ω=0,2. 3) Каким должен быть объем выборки для того, чтобы можно было гарантировать с вероятностью p=0.954, что пределы возможной средней ошибки выборки (средней цены покупки) не превзойдут 1,6 тыс. руб., а возможной ошибки доли (частости) не превзойдут 0,04, если по предыдущим обследованиям известно, что ω=0,2.
Решение. Для решения всех трех задач необходимо найти среднюю общую стоимость одной покупки и общую дисперсию:
Средняя из частных внутригрупповых дисперсий
1) Для расчета величины ошибки используем формулу предельной ошибки средней выборочной и подставим в нее все необходимые значения.
t=2 при Р=0,954 (из таблицы) N=4000, т.к. осуществлен десятипроцентный отбор и n=400 Вывод: средняя цена покупки в генеральной совокупности будет
Хген=36 ± 0,78 тыс. руб. 2) В пункте 2 необходимо произвести расчеты по величине вероятности для цены покупки и для доли покупателей, поэтому из формул ошибок средней и доли необходимо вычислить величину коэффициента доверия t, а затем по таблицам найти значение вероятностей. а) б)
Вывод: Вероятность средней цены покупки велика (0,99), а вероятность доли покупателей практически равна нулю. 3) В третьем пункте предлагается рассчитать объемы выборки для очередного выборочного наблюдения. Для этого мы выбираем формулу из таблицы 5.2. и подставляем в нее все необходимые числовые значения. а) t=2 (из таблиц), Dx=1,6 б) Dw=0,04, w=0,2 Вывод: Для оценки средней цены покупки надо опросить 105 человек, а для оценки доли покупателей необходимо побеседовать с 200 покупателями.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.191.203 (0.011 с.) |

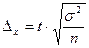 (5.6),
(5.6), (5.7)
(5.7) (5.8)
(5.8) ; (5.9)
; (5.9) ; (5.10)
; (5.10)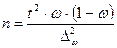 (5.11)
(5.11)



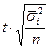




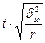








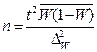

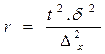



 , как это делается для большой выборки. Особенность малой выборки в том, что ее случайные ошибки не подчиняются закону нормального распределения.
, как это делается для большой выборки. Особенность малой выборки в том, что ее случайные ошибки не подчиняются закону нормального распределения. (5.12)
(5.12)
 – стандартная ошибка малой выборки.
– стандартная ошибка малой выборки.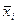
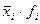
 280 ц/га.
280 ц/га.
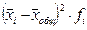
 ц/га.
ц/га. ц/га
ц/га ц/га
ц/га 287,34ц/га
287,34ц/га )
)
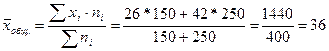 тыс. руб.
тыс. руб.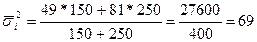
 тыс. руб.
тыс. руб. ; P(4,06)=0.99;
; P(4,06)=0.99; 
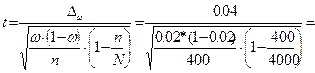 0,006
0,006