
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 1. Понятие средней величины.Содержание книги
Поиск на нашем сайте
Из истории статистики известно, что в 17-18 веках политические статистики (англ. Чарльз Давенант (1656-11714), англичанин Вилиям Пети (1623-1687), англичанин Грегори Кинг (1648-1712)) при проведении анализа результатов переписи населения во Франции и Англии использовали средние величины: средний душевой доход, средняя продолжительность жизни, средний размер семьи, среднее дневное пропитание одного взрослого работника и др. Понятие средней величины встречается в работах Адольфа Кетле (1796-1874), бельгийца по национальности и математика по образованию. В своей работе он отмечал: «Понятие о средней величине существует вне науки, которая придает ему определенность и точность» (1866 г.) Теория средних дальнейшее развитие получила в работах ученных 19 в. (Карл Пирсон (1857-1936), Макс Отто Лоренц (1876-1944), Родольфо Беннини (1862-1956) и др.). Большой вклад в развитие теории средних величин внесли советские ученые: А.Я. Боярский, В.Н. Старовский, В.И. Хотимский, Б.С. Ястремский и др. В 1930 г. в Москве был опубликован учебник этих авторов «Теория математической статистики». В результате сбора математической информации получаем базу данных, которую в последствии необходимо оценить. Если мы рассматриваем результаты деятельности сельскохозяйственных организаций по районам области, то возникает необходимость оценить значение анализируемых показателей в целом по области и в каждом районе. Если объектом исследования являются поля или фермы конкретного сельскохозяйственного предприятия, то необходимо оценить работу в полеводческих бригадах или на фермах и т.д. В таких случаях, когда оцениваются показатели в целом по нескольким объектам, прибегают к расчету средних значений анализируемых показателей. Однако выбор формул для расчета средних не так прост, как кажется на первый взгляд. Например, как рассчитать среднюю урожайность по культуре, если она занимает несколько полей с различной площадью? В экономических и технологических исследованиях возникает необходимость дать характеристику всей совокупности в целом, не рассматривая подробно состояние отдельных единиц этой совокупности. Например, есть необходимость оценить уровень развития молочного скотоводства по районам Гродненской области для принятия решения об инвестировании в строительство новых молочно-товарных ферм, где обеспечено содержание коров по современным интенсивным технологиям. Для чего и необходимо провести комплексное исследование совокупности молочно-товарных ферм в каждом районе.
Однако такой анализ требует особых знаний и умений для его проведения. Поэтому мы рассмотрим более простые задачи. Разберем понятие средней величины на конкретном примере. Задача. Группа студентов из 18 человек сдала экзамен по истории Беларуси при десятибалльной системе оценок знаний. Необходимо вычислить средний балл по этой дисциплине в группе, если получены следующие оценки: 9, 9, 9, 8, 6, 6, 9, 9, 6, 9, 8, 8, 8, 6, 6, 9, 8, 6. Средний балл можно вычислить двумя способами:
2) Подсчитаем, сколько каких оценок получили студенты. Тогда "девяток" – 7; "восьмерок" – 5; "шестерок" – 6; всего 18. Здесь средний балл можно вычислить иначе:
Как видно, в данном случае результат (средний балл) не зависит от способа расчета. Кроме того, второй способ быстрее дает результат, который отражает успеваемость группы, а не конкретного студента. Однако так бывает не всегда. Очень часто выбор формулы для расчета среднего значения анализируемого признака существенно влияет на качество исследования. Некоторые формы средних используются для расчетов в конкретных статистических методах (например, рядах динамики). При анализе статистической совокупности возникают два вопроса: 1) что отражает средний показатель; 2) как его вычислить. Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего признака в качественно однородной совокупности. Значит, средняя величина отражает или характеризует всю совокупность, а не отдельные ее единицы. По точности расчета (числу знаков после запятой) средняя величина может совпадать с индивидуальными значениями признака, а может не совпадать (например, средняя оценка в группе). Поскольку признак варьирует (изменяется), то совокупность должна быть однородной, то есть изменчивость показателя не должна быть сильной. Средние, характеризующие систему, совокупность в целом, называются системными или общими средними.
Средние, характеризующие подсистемы, типические группы или подгруппы, называются групповыми (см. дальше тему "Статистические группировки").
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.75 (0.01 с.) |

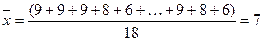 1)
1)



