Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 3. Приемы выравнивания рядов динамики.Содержание книги
Поиск на нашем сайте
Часто в рядах динамики сложно определить общую тенденцию развития. Второй задачей рядов динамики является выявление таких периодов развития, которые достаточно однородны по своим условиям и взаимодействиям связей между показателями. Под тенденцией понимается общее направление к росту, снижению или стабилизации уровня явления с течением времени. Тенденция по периодам может не совпадать с общей тенденцией. Иногда вообще сложно определить общую тенденцию. В этом случае прибегают к различным методам выравнивания ряда для определения его тенденции: 1) способу укрупнения интервалов; 2) сглаживанию ряда с помощью скользящей средней; 3) производят аналитическое выравнивание и получают уравнение тренда. Первый способ заключается в переходе от меньших временных интервалов к большим и расчете усредненных уровней ряда за укрупненный интервал. Временной промежуток для укрупнения интервала производят с учетом общей длины анализируемого ряда и величины исходных интервалов. Так, например, если исходный ряд содержит информацию за каждый месяц, то можно перейти к укрупненному интервалу величиной в квартал. Если представлена информация по годам, то «укрупнение» можно произвести за 2,3,4,5 лет в зависимости от длины исходного ряда. График этого ряда изображен на рисунке 7.2, где видно, что имеются периоды спада производства продукции и периоды подъема. Если рассмотреть только часть графика, начиная с 1998 года по 2005, то сложно установить общую тенденцию производства продукции данного вида. Поэтому более четко общая тенденция будет просматриваться, если произвести выравнивание ряда одним из методов. Так, использование метода укрупнения интервалов дает результаты, представленные в таблице 7.6 и 7.7. Например:
Таблица 7.6. Производство цельномолочной продукции в пересчете на молоко, тыс. тонн.
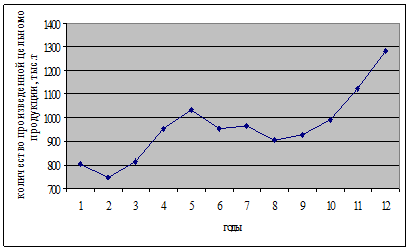
Рисунок 7.2. График динамики производства цельномолочной продукции в РБ
Таблица 7.7. Расчет производства цельномолочной продукции по укрупненным периодам (трехлетиям).
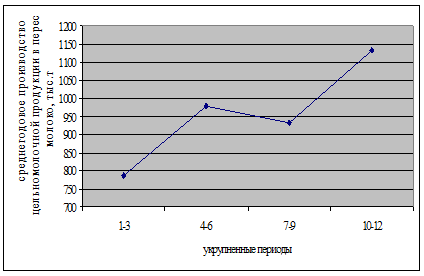
Алгоритм расчета: 801+744+813 = 2358; 2358/3=786,0 952+1032+954=2938; 2938/3=979,3 и т.д. Из последнего столбика таблицы 7.7 и рисунка 7.3 более четко видна тенденция к росту производства цельномолочной продукции.
Рисунок 7.3. График ряда, выровненного по укрупненным интервалам
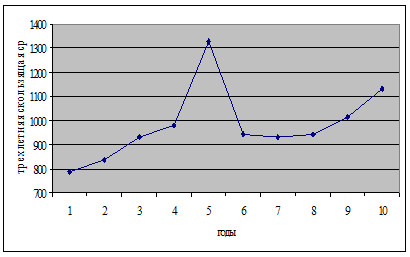
Второй способ заключается в последовательном расчете средних уровней за выбранный лаг времени, передвигая этот лаг на 1 интервал по времени t. Величину лага L выбирают произвольно в зависимости от длины анализируемого ряда: L = 2, 3, 4, …, n. Например, мы выберем трехлетний лаг. И тогда выровненный ряд можно представить в следующей таблице (7.8). Алгоритм расчета: 801+744+813=2358; 2358/3=786,0 744+813+952=2509; 2509/3=836,3 813+952+1032=2797; 2797/3=932,3 и т.д.
В настоящее время в основном используют третий метод, который рассмотрим в следующем вопросе.
Таблица 7.8 – Расчет трехлетней скользящей средней.
Рисунок 7.4. График ряда, выровненного по скользящей средней
В 4. Тренд. Аналитическое выравнивание ряда. Прогнозы по тренду. Самые точные результаты выравнивания ряда динамики дает аналитическое выравнивание, с помощью которого строят математическое уравнение, наилучшим образом описывающее тенденцию изменения показателя. Понятие об уравнении тенденции динамики ввел в 1902 году английский ученый Р.Гукер. Он предложил называть такое уравнение трендом (the trend). Под трендом понимают уравнение линии во времени, вдоль которой расположена ломаная ряда динамики. Этапы построения тренда: 1. Выявляют этапы развития явления (спады, подъемы, однородные участки и т.д.). 2. Анализируют показатели ряда динамики на этих этапах и выбирают вид уравнения (вид тренда). 3. Вычисляют параметры тренда, используя метод наименьших квадратов.
4. Оценивают адекватность уравнения развитию анализируемого показателя, оценивая колеблемость фактических уровней ряда вокруг теоретических, т.е. вычисленных по тренду. Рассмотрим 3-ий этап на простейшем примере, когда трендом является уравнение прямой линии. Будем искать уравнение в виде:
где t – параметр времени; Yt – соответствующие времени уровни ряда, Ŷt– выровненные уровни ряда, т.е. вычисленные по тренду. Исходную информацию и расчетные показатели представим в виде таблицы 7.9. Используя метод наименьших квадратов, построим систему уравнений:
Таблица 7.9. Схема таблицы для расчета параметров тренда
Решение этой системы позволит найти значения параметров уравнения. Если уравнение построено качественно, то åYi = Σ Ŷt. Эти расчеты можно упростить, если иначе производить номерацию параметра t. Ее нужно произвести следующим образом: начало отсчета должно находиться в середине анализируемого ряда. Если количество точек нечетное, то в середине ряда t ставим 0; если количество точек четное, то нуль выбрасывается. К началу ряда счет идет со знаком «–», к концу – со знаком «+», тогда åt становиться равной 0 (т.е. åt=0).
Таблица 7.10. Схема номерации уровней ряда от середины ряда
Тогда в системе нормальных уравнений (7.12) исчезнут слагаемые, в которые входит сумма t (Σt=0), т.е. мы получим упрощенную систему
где n – количество точек анализируемого ряда. Отсюда:
Параметр а1 соответствует абсолютному приросту за единицу периода времени. Тенденции или тренды могут быть выражены в виде кривых. Это могут быть: парабола, ветка гиперболы, экспонента или показательная кривая, логарифмическая линия и т.д. Виды трендов в виде кривых и их построение рассмотрим ниже. Прогноз по тренду. Используя уравнение можно построить точечный прогноз на последующие периоды времени, подставляя в уравнение тренда (7.11) номера t, следующие за последним фактическим номером, используемым при построении тренда. Например:
Таблица 7.11. Схема расчета прогноза при различной номерации показателей ряда динамики
Параметры а0 и а1 в уравнении тренда, построенных различным способом нумерации t, будут отличаться, а прогнозы будут совпадать. Оценка точности тренда. В экономическом анализе необходимо оценить силу разброса фактических точек вокруг расчетных (трендовых). Это оценивается по величине остаточного среднеквадратического отклонения и коэффициенту вариации:
Чем меньше значения σост. и V, тем лучше тренд отражает тенденцию изменения показателя. Имея оценку качества тренда, производят оценку качества прогноза на перспективу.
Для точечного прогноза по тренду, также как и для выборочного наблюдения, необходимо оценить среднюю ошибку прогноза. Для линейного тренда средняя ошибка прогноза рассчитывается:
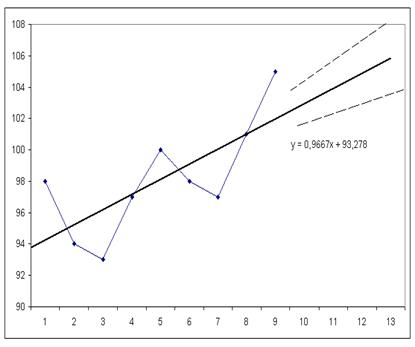
Рисунок 7.5. Точечное и интервальное прогнозирование
Доверительный интервал или предельная ошибка прогноза равна средней ошибке умноженной на коэффициент доверия t-Стьюдента, при доверительных вероятностях p=0,90; 0,95; 0,99. Строчку в таблицах находим по числу степеней свободы тренда n – m.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |


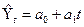 (7.11)
(7.11)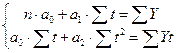 (7.12)
(7.12)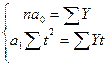 (7.13)
(7.13)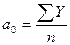 (7.14)
(7.14)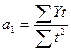 (7.15)
(7.15)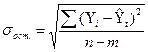 (7.16)
(7.16)
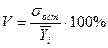 (7.17)
(7.17) где Yi – средний уровень ряда.
где Yi – средний уровень ряда.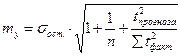 (7.18)
(7.18)