
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 7. Классификация агрегатных индексов по содержанию.Содержание книги
Поиск на нашем сайте
Рассмотрим деление агрегатных индексов на качественные и количественные на примере индексов объёма товарооборота переменного состава и его разложения на индексы постоянного состава (формула 8.12).
7.1)
Это агрегатный индекс переменного состава. Кроме того, он будет объёмным (или количественным) в силу того, что здесь индексируется (изменяется) обобщающий объёмный показатель – товарооборот (выручка или стоимость товара). Для индексов постоянного состава этот вопрос решается иначе. Отнесение индекса к количественному или качественному зависит от того, какой фактор (количественный или качественный) индексируется (изменяется).
7.2)
– Это агрегатный индекс постоянного состава. Он показывает, во сколько раз изменился товарооборот (выручка) за счет изменения количества и структуры товара. В индексе количества и структуры товара отражена динамика объёмного показателя (q), поэтому этот индекс является объёмным или количественным.
7.3)
– Данный агрегатный индекс цен постоянного состава отражает изменение выручки за счет изменения цен. В индексе цен определяющей является динамика качественного показателя – цены (р) и влияние её на товарооборот, поэтому этот индекс является качественным. В 8. Классификация агрегатных индексов по базе сравнения. Если в индексном анализе сравниваются показатели за два периода, то эти индексы носят название базисных. Если система индексов построена на показателях, взятых как минимум за 3 периода и более, причём каждый последующий показатель сравнивается как с начальным уровнем, взятым за базу сравнения, так и с предыдущим, то первые из них индексы являются базисными, а вторые – цепными. Кроме того, при построении системы необходимо учитывать состав индексов, в зависимости от цели исследования и базы сравнения показателей. В формулах это может выглядеть следующим образом. Базисные индексы выручки (стоимости товара) переменного состава:
Цепные индексы выручки (стоимости товара) переменного состава:
Можно построить системы цепных и базисных индексов постоянного состава. Например, базисные индексы физического объема постоянного состава:
цепные индексы физического объема постоянного состава:
Кроме того, между цепными и базисными индексами установлены математические зависимости, которые могут быть использованы в конкретном экономическом анализе. Зная базисные индексы, можно построить цепные и наоборот.
В 9. Средние индексы. В разной научной и учебной литературе предлагаются кроме агрегатных другие формы индексов. В технико-экономическом анализе часто решается задача исследования поведения индивидуальных значений показателей, входящих в модель и их влияния на результативные показатели. Например, как влияют на выручку или товарооборот индивидуальные изменения цены и объема каждого вида продукции. И здесь используется другая форма построения индексов – общие средние индексы из индивидуальных индексов.Такая форма индексов получила название средних индексов: средние арифметические и средние гармонические. Рассмотрим эти формы построения общих индексов. 1) Средний арифметический индекс физического объема продукции получим в том случае, если частотой (или повторяемостью) для индивидуального индекса iq будет служить объем товарооборота q0p0. Построенный индекс будет равен агрегатному индексу количества и структуры товара, т.е.
Это равенство среднего и агрегатного индексов следует и соотношения
При построении среднеарифметического индекса цен необходимо определиться с весами (в нашей формуле это веса Г. Пааше). Тогда построенный средний арифметический индекс цен будет равен агрегатному индексу цен Пааше.
Данное равенство индексов обеспечивается за счет соотношения:
2) Средний гармонический индекс. Средний гармонический индекс цен с весами Г.Пааше будет иметь вид:
Равенство среднего гармонического индекса и агрегатного индекса обеспечивается соотношением:
Аналогично средний гармонический индекс количества и структуры товара будет построен следующим образом.
Данное равенство обеспечивается соотношением
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 (8.19)
(8.19)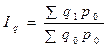 (8.20)
(8.20) (8.21)
(8.21) ;
;  ;…;
;…;  (8.22)
(8.22) ;
;  ; …;
; …;  (8.23)
(8.23) ;
;  ;...;
;...;  (8.24)
(8.24) ;
;  …;
…;  (8.25)
(8.25)
 (8.26)
(8.26)
 (8.27)
(8.27)
 (8.28)
(8.28)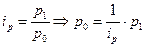
 =
=  (8.29)
(8.29)



