
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В 7. Расчет параметров криволинейных уравнений.Содержание книги
Поиск на нашем сайте
Гипербола:
Степенная функция:
Парабола:
В 8. Оценка тесноты связи при криволинейных моделях. В отличие от линейной корреляционно-регрессионной зависимости, при криволинейных связях тесноту связи признаков определяют по индексам корреляции и детерминации. Смысл индексов тот же, что и коэффициентов корреляции и детерминации. Схема нахождения индекса детерминации: 1. Определяют общую дисперсию
2. Определяют меру колеблемости расчетных значений признака около среднего:
3. Определяют меру колеблемости результативных показателей вокруг теоретических значений, вычисленных по уравнению регрессии.
4. В математической статистике доказывают, что общая дисперсия равна факторной дисперсии плюс остаточная дисперсия:
Индексом детерминации i2 называется отношение факторной дисперсии к общей дисперсии, т.е.
Этот индекс объясняет, какая часть вариации результативного признака (Y) объясняется вариацией факторного признака (X). Индекс детерминации может быть выражен в процентах. 5. Индекс корреляции равен корню квадратному из индекса детерминации взятого в долях (а не в процентах):
Индекс корреляции всегда положителен и не может указывать направление связи. Например: при параболической связи признаков одна ветвь показывает возрастание, другая убывание факторов и общего направления быть не может. 6. Достоверность индексов корреляции и детерминации при криволинейных связях оценивают по критерию Фишера:
где: n — число единиц в совокупности, m — число параметров уравнения. F расчетное сравниваем с F табличным. Строку в таблицах находим по значению
столбец по значению
Если F расчетное больше F табличного, то нуль-гипотеза отвергается и принимается утверждение, что криволинейная связь в виде полученного уравнения регрессии, индекс корреляции и детерминации достоверны. Если же соотношение Fрасч.<Fтабл., то наша модель недостоверна.
В 9. История развития многофакторного корреляционно-регрессионного анализа. Начало корреляционного и регрессионного анализа относится ко второй половине ХIХ века и связано с именем двоюродного брата Ч. Дарвина – Френсисом Гальтоном (1822–1911). Он ввел понятие «закона регрессии», связав его со средним снижением роста сыновей по сравнению с ростом отцов (1899 г). Ему же принадлежит введение числовой меры, оценивающей силу связи показателей (корреляцию). Поэтому началом разработки корреляционно-регрессионного анализа ученые–статистики считают статью Ф. Гальтона «Регрессия, наследственность и панмиксия» (1896 г), в которой автор «дал определение корреляции, построил теоретическую модель совместного измерения двух переменных, ввел понятие линии регрессии и корреляционного индекса «r».
Экономистами и математиками разработаны различные модели, оценивающие влияние нескольких факторов на результат. Например, в США в 1929 г. при анализе развития обрабатывающей промышленности за 1899–1922 гг. была построена мультипликативная производственная функция, отражающая зависимость выхода продукции от затрат живого труда и наличия капитала, которая получила название функции Кобба-Дугласа (там же, с.176):
У= а Lα Kβ, (6.39)
где У – объем выпускаемой продукции, а – коэффициент размерности, L – объем затрат живого труда или численность работников, К – объем капитала (основного или совокупного), α и β – коэффициенты эластичности производства продукции по труду и капиталу. Для сельского хозяйства данную модель можно расширить, включив в нее еще один важный ресурс – это площадь сельскохозяйственных угодий (S) с соответствующим коэффициентом эластичности. Тогда данная функция будет иметь вид:
У=аLαKβSγ, (6.40)
Существуют и другие нелинейные модели, отражающие различные связи факторов, некоторые из которых рассматриваются в курсе «Планирование и прогнозирование». Однако большинство из них не могут быть интерпретированы системой экономических параметров и сложны в экономическом обосновании. Например, что может отражать экономический логарифм производительности труда или производительность труда в степени n и так далее? То есть модели могут быть использованы для прогнозов без экономической интерпретации параметров. Наилучшим образом экономически интерпретируется многофакторные линейные модели вида:
где: n – отражает число факторов.
При составлении модели встает вопрос отбора факторов, которые могут быть включены в многофакторную модель. Как правило, имеется таблица с базой данных, где указаны числовые значения факторов интересующих исследователя. Общий вид такой таблицы с информацией о значениях технико-экономических показателей следующий:
Таблица 6.3. База данных для исследования связей факторов
При исследовании необходимо решить целый ряд проблем, одна из которых заключается в отборе факторов для их включения в модель (уравнение регрессии). Здесь существенную роль играют знания исследователя об экономических закономерностях развития процессов и явлений, знания экономики конкретной отрасли (сельского хозяйства легкой и тяжелой промышленности, транспорта и т.д.). После сбора информации и проведения ее априорного анализа можно провести расчеты, позволяющие достаточно качественно отобрать факторы для проведения корреляционно-регрессионного анализа. Для отбора факторов для модели часто используют матрицу парных коэффициентов корреляции, расчет и интерпретация которых рассматривалась в вопросах 5 и 6 темы.
Таблица 6.4. Матрица парных коэффициентов корреляции
Матрицу используют следующим образом: По строке Y анализируют значения парных коэффициентов корреляции rij и отбирают в модель те факторы, для которых riy>0,2. Используя остальные строки матрицы, устанавливают наличие или отсутствие мультиколлинеарности факторов. Если выявляется наличие таких пар факторов, то в модель включают только один из них. Факторы являются мультиколлинеарными, если связь между ними близка к функциональной или функциональна. Например, производительность труда и трудоемкость –показатели обратные друг другу, и для них парный коэффициент корреляции равен единице. В модель можно включить только один из этих факторов. Можно считать, что фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффициентов регрессии, не изменяя суммы квадратов остатков, то есть:
Если при включении в модель факторного признака увеличивается величина множественного коэффициента корреляции и детерминации, а коэффициенты регрессии меняются незначительно, то данный признак существенен, и его включение в уравнение регрессии обязательно. В 10. Нахождение параметров уравнения многофакторной корреляционно-регрессионной модели. Параметры уравнения регрессии (6.41), то есть коэффициенты регрессии ai и свободный член a0 находят из системы (6.43) нормальных уравнений по методу наименьших квадратов.
Данная система может быть решена методом Гаусса или матричным методом. a0 –- свободный член, который отражает объем вариации результативного показателя за счет вариации факторов, не включенных в модель (в том числе и случайную вариацию); ai – называют частными коэффициента регрессии в отличие от парных. Частный коэффициент регрессии показывает, на сколько единиц в среднем изменится результативный показатель (У) с учетом знака, при изменении факторного признака (Xi) на единицу своего измерения при условии, что другие учтенные в модели факторы остаются неизменными.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.243 (0.007 с.) |

 (6.21)
(6.21)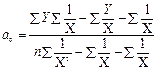 (6.22)
(6.22) (6.23)
(6.23) (6.24)
(6.24) (6.25)
(6.25)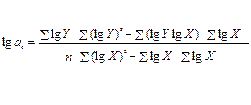 (6.26)
(6.26)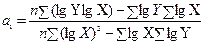 (6.27)
(6.27) (6.28)
(6.28) (6.29)
(6.29) (6.30)
(6.30) (6.31)
(6.31) (6.32)
(6.32) (6.33)
(6.33) (6.34)
(6.34) (6.35)
(6.35) (6.36)
(6.36) ; (6.37)
; (6.37) (6.38)
(6.38) (6.41)
(6.41) = const (6.42)
= const (6.42) (6.43)
(6.43)


