
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение системы комплексных чисел
Вопрос 1 Построение системы комплексных чисел Самые простые числа — это натуральные, они обозначаются буквой 1, 2, 3, 4, 5, 6, … С помощью этих чисел мы считаем разные объекты. Натуральные числа мы можем складывать и умножать. Целые числа, обозначаемые
Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы дробные числа
Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга и снова получать рациональное число (конечно, на ноль делить при этом нельзя). Следующее множество чисел, расширяющее множество рациональных чисел — это действительные (вещественные) числа Существует ещё одно расширение чисел — комплексные числа. В комплексных числах можно брать корни из отрицательных чисел. Комплексные числа хороши ещё тем, что любой многочлен имеет среди этих чисел корень. Например, уравнение
Не имеет корней в действительных числах, но имеет корень в комплексных числах.
Рассмотрим множество М{(а,в)(а,в)еR} Введем на М операцию + Длю любого а,б,с,деР (а,б)+(с,д)=(а+с;б+д); Свойства этой операции 1) (а,б)+(с,д)=(с;д)+(а,б) 2 (а,б)+(с,д)+(е,ф)=((а+с)+е)+((б+д)+ф)=(а,б)+((с,д)+(е+ф))
Вопрос 2 Алгебраическая форма комплексного числа Числа вида z=a+bi, где а и b действительные числа, i – мнимая единица, называются комплексными. Обозначение a=Rez, b=Imz. Запись комплексного числа в виде a+bi называется алгебраической формой записи комплексного числа. Число a называется действительной частью, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части. Возможны случаи, когда действительные числа а и b могут быть равны 0. Если а=0, то комплексное число bi называется чисто мнимым. Если b=0, то комплексное число a+bi равно а и называется действительным. Если а=0 и b=0 одновременно, то комплексное число 0+0i равно нулю.
Число i называется мнимой единицей, а равенство i2=-1 считается определением мнимой единицей.
Вопрос 3 Действия над комплексными числами в алгебраической форме Сложение Чтобы найти сумму двух комплексных чисел, надо отдельно сложить их действительные и мнимые части:
Вычитание Вычитание комплексных чисел определяют как действие, обратное сложению. Поэтому действительная и мнимая части разности z1 − z2 равны, соответственно, разности действительных и мнимых частей чисел z1 и z2. Умножение Комплексные числа умножают по правилам умножения многочленов, принимая во внимание, что i2 = −1:
Деление Чтобы разделить комплексное число z1 на число z2 не равное 0 в алгебраической форме, надо числитель и знаменатель дроби z1/z2 умножить на число z2, комплексно-сопряженное знаменателю:
Вопрос 4 Вопрос 5 Тригонометрическая форма комплексного числа Часто бывает тригонометрическая форма записи комплексного числа. Пусть
Отсюда получается
Такая форма называется тригонометрической формой записи комплексного числа. Таким образом, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Вопрос 6,7 Действия над числами в тригонометрической форме Вопрос 8 Вопрос 9 Понятие дифференциального уравнения первой степени Обыкновенным дифферинциальным уравнением первой степени, называется уравнения вида F(x,y,y’)=0; Связывающее независимые переменные х, искомую функцию у и её производную у’ Y=y(x); y’=y’(x)
Вопрос 10 Вопрос 11 Понятие решения дифференциального уравнения Решением д.у. называется функция y=u(x), которая при постановке её в уравнение превращает его в тождество
Вопрос 12 Интегральная прямая
График уравнения y=u(x), называется интегральной прямой
Вопрос 13 Вопрос 14. Залача Коши. Теорема Коши.
Задача отыскания решений д.у. первого порядка, удовлетворяющее заданному начальному условию
Y(x0)=y0, называется задачей Коши
Т. Коши Пусть в д.у. y’=f(x’y), функция f(x,y) и её частная производная f’y(x;y), не прерывна в некоторой области Д, тогда любая точка М(х0.у0)еД существует единственное решение у=у(х), удовлетворяющее начальному условию у0=у(х0)
Вопрос 15 Вопрос 16 Вопрос 1 Построение системы комплексных чисел Самые простые числа — это натуральные, они обозначаются буквой 1, 2, 3, 4, 5, 6, … С помощью этих чисел мы считаем разные объекты. Натуральные числа мы можем складывать и умножать. Целые числа, обозначаемые
Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы дробные числа
Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга и снова получать рациональное число (конечно, на ноль делить при этом нельзя). Следующее множество чисел, расширяющее множество рациональных чисел — это действительные (вещественные) числа Существует ещё одно расширение чисел — комплексные числа. В комплексных числах можно брать корни из отрицательных чисел. Комплексные числа хороши ещё тем, что любой многочлен имеет среди этих чисел корень. Например, уравнение
Не имеет корней в действительных числах, но имеет корень в комплексных числах.
Рассмотрим множество М{(а,в)(а,в)еR} Введем на М операцию + Длю любого а,б,с,деР (а,б)+(с,д)=(а+с;б+д); Свойства этой операции 1) (а,б)+(с,д)=(с;д)+(а,б) 2 (а,б)+(с,д)+(е,ф)=((а+с)+е)+((б+д)+ф)=(а,б)+((с,д)+(е+ф))
Вопрос 2
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.117.95 (0.009 с.) |
 :
: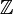 , расширяют множество натуральных чисел — добавляют нуль и отрицательные числа. Наличие отрицательных чисел позволяет нам вычитать любое число из любого, тогда как «живя» в натуральных числах, при вычитании мы должны были всегда следить, чтобы из большего вычиталось меньшее. Вот примеры целых чисел:
, расширяют множество натуральных чисел — добавляют нуль и отрицательные числа. Наличие отрицательных чисел позволяет нам вычитать любое число из любого, тогда как «живя» в натуральных числах, при вычитании мы должны были всегда следить, чтобы из большего вычиталось меньшее. Вот примеры целых чисел:
 . Их так же называют рациональными:
. Их так же называют рациональными:
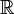 . Действительные числа – это рациональные и иррациональные числа. Иррациональное число – это число, которое нельзя представить в виде отношения двух чисел. Например, корень из 2
. Действительные числа – это рациональные и иррациональные числа. Иррациональное число – это число, которое нельзя представить в виде отношения двух чисел. Например, корень из 2


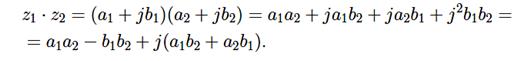

 и φ = arg z. Тогда по определению аргумента имеем:
и φ = arg z. Тогда по определению аргумента имеем:



