
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнений с комплексным переменнымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим сначала простейшее квадратное уравнение z2 = a, где а - заданное число, z - неизвестное. На множестве действительных чисел это уравнение: 1) имеет один корень z = 0, если а = 0; 2) имеет два действительных корня z1,2 = 3) не имеет действительных корней, если а<0. На множестве комплексных чисел это уравнение всегда имеет корень. Задача 1. Найти комплексные корни уравнения z2 = a, если: 1)а = -1; 2)а = -25; 3)а = -3. 1)z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2 - i2 = 0. Отсюда, раскладывая левую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i.Ответ. z1,2 = 2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение: z2 = (-1)25, z2 = i2 52, z2 - 52 = 0, (z-5i)(z+5i) = 0, откуда z1 = 5i, z2 = -5i.Ответ.z 1,2 = 3) z2 = -3, z2 = i2( Вообще уравнение z2 = a, где а < 0 имеет два комплексных корня: Z1,2= Используя равенство i2 = -1, квадратные корни из отрицательных чисел принято записывать так: Z1,2 = Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 = Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13. Число 4- это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13- свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 - корни уравнения az2+bz+c = 0, z1+z2 = - Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i. Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим P=-(z1+z2)=2, q=z1z2=5. Ответ z2-2z+5=0. Вопрос Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = arg z. Тогда по определению аргумента имеем: Отсюда получается где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось; Arg z - множество аргументов числа z: Вопрос 1 сложение При сложении и вычитании складываются отдельно действительные части чисел, и отднльно мнимые части чисел и опять же число записывается в виде z=a+bi Вопрос Формула Муавра и извлечение корней из комплексных чисел
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |


 , если а>0;
, если а>0; )2, z2 - (
)2, z2 - ( = i,
= i,  = i
= i 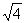 = 2i,
= 2i,  = i
= i  . Итак,
. Итак,  0, имеет корни. Эти корни находятся по известной формуле:
0, имеет корни. Эти корни находятся по известной формуле: .
. =
=  =
=  =
=  =2
=2 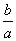 , z1z2 =
, z1z2 =  .
.
 здесь
здесь  – биномиальные коэффициенты.
Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.
– биномиальные коэффициенты.
Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.



