
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация комплексного числаСодержание книги
Поиск на нашем сайте Вопрос Множество - это совокупность, класс отличающихся друг от друга объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества. К множеству целых чисел относятся все положительные или отрицательные числа, не являющиеся дробями, и нуль. Например,...-3, -2, -1, 0, 1, 2, 3... Множество целых чисел бесконечно. Положительные целые числа также называются натуральными. Записать множество целых чисел можно так Z={... -3, -2, -1, 0, 1, 2, 3...} Вопрос
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел. Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i 3 = 3 i. Чисто мнимое число i 1 = 1 i = i обладает удивительным свойством:
Вопрос Рассмотрим решение квадратного уравнения х2 +1 = 0. Отсюда х2 = -1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом, i2 = -1, откуда i = Числа вида 4+3i и 4-3i называют комплексными числами. В общем виде комплексное число записывается а + bi, где a и b- действительные числа, а i – мнимая единица. Число а называется действительной частью комплексного числа, bi-мнимой частью этого числа, b- коэффициентом мнимой части комплексного числа. Сложение комплексных чисел. Суммой двух комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = (a+c) + (b+d)i. Числа a + bi и a-bi называются сопряженными. Их сумма равна действительному числу 2а, (а+bi) + (а-bi) = 2а. Числа а+bi и -a-bi называются противоположными. Их сумма равна нулю. Комлексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi = c+di, если a = c, b = d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0,b = 0. Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a - действительное число. Если а = 0, b Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и с + di называется комплексное число х + уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что х = а-с, у = b-d. Значит, (а+bi) - (c+di) = (a-c) + (b-d)i. Произведение комплексных чисел z 1= a + bi и z2 = c + di называется комплексное число z = (ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac - bd) + (ad + bc)i. Легко проверить, что умножение комплексных чиcел можно выполнять как умножение многочленов с заменой i2 на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению. Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a + bi)(a - bi) = a2 + b2 Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di) = Степень числа i является периодической функцией показателя с периодом 4. Действительно, i2 = -1, i3 = -i, i4 = 1, i4n = (i4)n = 1n = 1, i4n+1 = i, i4n+2 = -1, i4n+3 = -i. Вопрос Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = arg z. Тогда по определению аргумента имеем: Отсюда получается где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось; Arg z - множество аргументов числа z: Вопрос 1 сложение При сложении и вычитании складываются отдельно действительные части чисел, и отднльно мнимые части чисел и опять же число записывается в виде z=a+bi Вопрос Формула Муавра и извлечение корней из комплексных чисел
Вопрос Решение уравнений высших степеней. В общем случае уравнение степени выше четвертой не разрешимо в радикалах. Однако, иногда можно отыскать корни уравнения высшей степени, представив его в виде призведения многочленов степени не выше четвертой. Таким образом, разложение многочлена на множители является основным методом решения таких уравнений, поэтому, рекомендуем подробно изучить этот раздел, прежде чем двигаться дальше. Достаточно часто рассматриваются уравнения высших степеней с целыми коэффициентами. В этом случае можно попытаться найти рациональные корни и понизить степень исходного уравнения хотя бы до четвертой делением многочлена на многочлен. На их решении и остановимся. Уравнения высших степеней с целыми коэффициентами. Любое уравнение вида можно свести к приведенному уравнению той же степени домножив обе его части на и выполнив замену переменной Полученные коэффициенты тоже будут целыми. Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида Алгоритм решения. Находим целые корни уравнения. Целые корни уравнения, i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена. То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде, где - корень уравнения, а - частное от деления на. Продолжаем подставлять выписанные ранее делители в уравнение, начиная с (так как корни могут повторяться). Как только получаем тождество, то корень найден и уравнение предстает в виде, где - частное от деления на. И так продолжаем перебор делителей, начиная с. В итоге найдем все m целых корней уравнения и оно представится в виде, где - многочлен степени n-m. Весь этот процесс удобно представлять в виде схемы Горнера. Дробных корней приведенное уравнение с целыми коэффициентами иметь не может. Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения любым способом.
http://www.cleverstudents.ru/equations_of_higher_degree.html Вопрос Интегрирование дробно-рациональных функций. Определение дробно-рациональной функции. Определение 1. Целой функцией называется многочлен (полином).
Определение 2. Дробно-рациональной функцией называется дробь, числителем и знаменателем которой являются многочлены.
Определение 3. Дробно-рациональная функция называется неправильной рациональной дробью, если степень числителя не меньше степени знаменателя(n m). Определение 4. Дробно-рациональная функция называется правильной, если степень числителя меньше степени знаменателя. Теорема: Любую неправильную рациональную дробь можно представить в виде суммы целой функции и правильной рациональной дроби.
Постановка задачи интегрирования дробно-рациональной функции.
Простейшие рациональные дроби. Простейшими рациональными дробями являются рациональные дроби: 1) 2) 3) Выделяем полный квадрат и делаем замену переменной:
Тогда интеграл примет вид:
Делаем обратную замену переменной и получаем окончательный ответ. Разложение правильной рациональной дроби на сумму простейших дробей. Дана правильная дробь:
Теорема 1. Если знаменатель Q(x) имеет любые корни, то правильная дробь разлагается на сумму простейших дробей 1 и 2 типа. Интегрирование правильной рациональной дроби.
Вопрос Определение Областью определения функции (выражения f(x)) называют множество всех значений x, для которых функция (выражение) имеет смысл. Область определения функции обозначается как или D(f) или D(y) Вопрос 1. Метод оценки (границ). Для нахождения множества значений функции сначала находят множество значений аргумента, затем, используя свойства неравенств, отыскивают соответствующие наименьше и наибольшее значения функции функции. Если есть возможность путем тождественных преобразований получить функцию, которая на всей области определения или на заранее заданном множестве является непрерывной и либо только возрастающей либо только убывающей, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Пример 1. Найдите множество значений функции y=5 - Из определения квадратного корня следует, что 4 - x2 Возведем в квадрат каждое из этих двойных неравенств, в результате получим 0 - 4 0 t = 4 - x2, где 0 Функция y = Множество значений функции y = 5 -
Пример 2. Найти множество значений функции y = 5 - 4sinx. Из определения синуса следует, -1 -4 1 Так как данная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением на всей области определения, если таковые существуют. В данном случаее множество значений функции y =5 - 4sinx есть множество [1; 9].
Пример 3. Найти множество значений функции y = sinx + cos x. Преобразуем выражение sinx + cos x = sinx +sin( Из определения косинуса следует -1 -1 - Так как данная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением, если таковые существуют, множество значений функции y = y = sinx + cosx есть множество чисел [-
Пример 4. Найти множество значений функции y = 3sinx + 7cos x. Преобразуем выражение 3sinx + 7cos x. Заметим, что 32 + 72 = 9 + 49 = 58 = Из определения синуса следует, что при любом х справедливо неравенство -1 -1 sin( Множество значений функции y = 3sinx + 7cos x является множество [ - Вопрос Пасаны извени но это реально большая пизда нет у меня вариантов как это найти)) Вопрос Вопрос Вопрос Вопрос No))) Вопрос 1.Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. 2.Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй. 3.Произведение суммы двух величин на их разность равно разности их квадратов. 4.Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй. 5.Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй. 7. Произведение разности двух величин на неполный квадрат суммы равно разности их кубов. Всем удачи чуваки)) Вопрос Множество - это совокупность, класс отличающихся друг от друга объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества. К множеству целых чисел относятся все положительные или отрицательные числа, не являющиеся дробями, и нуль. Например,...-3, -2, -1, 0, 1, 2, 3... Множество целых чисел бесконечно. Положительные целые числа также называются натуральными. Записать множество целых чисел можно так Z={... -3, -2, -1, 0, 1, 2, 3...} Вопрос
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел. Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i 3 = 3 i. Чисто мнимое число i 1 = 1 i = i обладает удивительным свойством:
Геометрическая интерпретация комплексного числа Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой. Расстояние r точки z от нулевой точки, т. е. число
называется модулем комплексного числа z и обозначается символом | z |. Число
называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном r углы, отличающиеся на Числа r и θ называют полярными координатами комплексного числа z. В этом случае z = (x, y) = (r cos θ, r sin θ) = r (cos θ + i sin θ) называется тригонометрической формой комплексного числа. Если z 1 = (r 1 cos θ 1, r 1 sin θ 1), z 2 = (r 2 cos θ 2, r 2 sin θ 2), то z 1 z 2 = (r 1 r 2 cos(θ 1 + θ 2), r 1 r 2 sin(θ 1 + θ 2)),
Для n -й степени числа z = (r cos θ, r sin θ) формула приобретает вид zn = (rn cos nθ, rn sin nθ). При r = 1 соотношение приобретает вид zn = (cos nθ, sin nθ) и называется формулой Муавра. Корень n -й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
Вопрос Рассмотрим решение квадратного уравнения х2 +1 = 0. Отсюда х2 = -1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом, i2 = -1, откуда i = Числа вида 4+3i и 4-3i называют комплексными числами. В общем виде комплексное число записывается а + bi, где a и b- действительные числа, а i – мнимая единица. Число а называется действительной частью комплексного числа, bi-мнимой частью этого числа, b- коэффициентом мнимой части комплексного числа. Сложение комплексных чисел. Суммой двух комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = (a+c) + (b+d)i. Числа a + bi и a-bi называются сопряженными. Их сумма равна действительному числу 2а, (а+bi) + (а-bi) = 2а. Числа а+bi и -a-bi называются противоположными. Их сумма равна нулю. Комлексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi = c+di, если a = c, b = d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. z = a + bi = 0, если a = 0,b = 0. Действительные числа являются частным случаем комплексных чисел. Если b = 0, то a + bi = a - действительное число. Если а = 0, b Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a + bi и с + di называется комплексное число х + уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что х = а-с, у = b-d. Значит, (а+bi) - (c+di) = (a-c) + (b-d)i. Произведение комплексных чисел z 1= a + bi и z2 = c + di называется комплексное число z = (ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac - bd) + (ad + bc)i. Легко проверить, что умножение комплексных чиcел можно выполнять как умножение многочленов с заменой i2 на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению. Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a + bi)(a - bi) = a2 + b2 Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di) = Степень числа i является периодической функцией показателя с периодом 4. Действительно, i2 = -1, i3 = -i, i4 = 1, i4n = (i4)n = 1n = 1, i4n+1 = i, i4n+2 = -1, i4n+3 = -i.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.014 с.) |






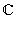 . Мы установили, что
. Мы установили, что 


 . Решение квадратного уравнения, например, х2 – 8х + 25 = 0, можно записать следующим образом: х = 4
. Решение квадратного уравнения, например, х2 – 8х + 25 = 0, можно записать следующим образом: х = 4 
 = 4
= 4  = 4
= 4 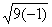 = 4
= 4  0, то a + bi = bi – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
0, то a + bi = bi – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
 =
= 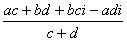 =
=  +
+ 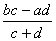 i.
i.
 здесь
здесь  – биномиальные коэффициенты.
Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.
– биномиальные коэффициенты.
Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.


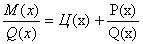
 - задача свелась к интегрированию правильной рациональной дроби.
- задача свелась к интегрированию правильной рациональной дроби.





 (1)
(1) сумме интегралов от простейших дробей (см. формулу 1 из 9.4).
сумме интегралов от простейших дробей (см. формулу 1 из 9.4). .
. 0, решая квадратичное неравенство получаем, что -2
0, решая квадратичное неравенство получаем, что -2  x
x  на указанном промежутке непрерывна и возрастает, поэтому свои наименьшее и наибольшее значения принимает на концах промежутка и, следовательно, 0
на указанном промежутке непрерывна и возрастает, поэтому свои наименьшее и наибольшее значения принимает на концах промежутка и, следовательно, 0  - x) =
- x) = )cos(x +
)cos(x + 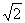 cos(x +
cos(x + 
 (
( sinx +
sinx +  cosx).
cosx). что cos
что cos 





 , соответствуют одному и тому же числу. В этом случае записываем
, соответствуют одному и тому же числу. В этом случае записываем 

 называем главным значением аргумента.
называем главным значением аргумента.






 (1)
(1)


