
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод применения свойств непрерывной функции.Содержание книги
Поиск на нашем сайте Среди числовых значений, принимаемых на заданном отрезке непрерывной функцией, всегда имеется как наименьшее pначение m, так и наибольшее значение М. Множество значений функции заключено между числами m и M. Это основные утверждения положенны в основу поиска множества значений функции в следующем примере. Пример 5. Найти множество значений функции y = 2sinx + cos2x на отрезке [0; p]. Решение. D(y) = R. Данная функция на всей области определения непрерывна, поэтому на отрезке [0; p] существуют такие точки, в которых функция принимает свои наименьше и наибольшее значения. Эти точки либо критические, либо концы отрезка. 1) найдем производную данной функции 2) y' = 2cosx - 2 sin2x = 2cosx - 4sinxcosx = 2cosx(1 - 2sinx) 3) Область определения производной R. 3) Найдем ее критические точки. y' = 0. 2cosx(1 - sinx) = 0, это уравнение равносильно совокупности двух уравнений: Отрезку [0; Вычисляем значение функции на концах промежутка и в критических точках: 3. Метод приведения к уравнению относительно х с параметром у. Возможна следующая схема применения этого метода: Пусть функция задана формулой y = f(x). 2) Рассматриваем функцию как уравнение с параметром у. 3) Выясняем при каких значениях у уравнение f(x) - y = 0 имеет хотя бы один корень. Полученное множество будет множеством значений заданной функции. Пример 6. найдите множество значений функции Решение. x2 + 5 > 0 при любом х, следовательно, D(y) = R. Рассматриваем формулу:
x2 (y - 1) + 4x + 5y + 1 = 0; 1) Если у = 1, то данное уравнение равносильно линейному уравнению 4х + 6 = 0, которое имеет один корень. Если у D/4 = 4 - (y - 1)(5y + 1) - 5y2 + 4y +5 5y2 - 4y - 5 D/4 = 4 + 25 = 29 y = 2 - Таким образом квадратное уравнение имеет корни,если параметр y Учитывая пункты 1) и 2), делаем вывод, что множество значений изучаемой функции - [2 - 4. Метод непосредственных вычислений. В случае, когда область определения функции содержит конечное число значений аргумента или количество значений не велико, или множество значений аргумента может быть описано с помощью конечного числа формул, так бывает в случае рассмотрения тригонометрических функций, обычно множество значений функции находят путем непосредственных вычислений. Пример 7. Укажите множество значений функции y = 11 - Решение. Найдем область определения данной функции. Так как в формуле задающей функцию есть квадратный корень, то согласно определению квадратного корня потребуем, чтобы подкоренное выражение было неотрицательным: 10х - х2 -25 -(х - 5)2 (х - 5)2 Вопрос Пасаны извени но это реально большая пизда нет у меня вариантов как это найти)) Вопрос Вопрос Ебенячаяя ссылка на презинтацию только есть)) http://www.google.ru/url?sa=t&rct=j&q=%D0%BF%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5+%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%BE%D0%B2+%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85+%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B9&source=web&cd=8&ved=0CE8QFjAH&url=http%3A%2F%2Farm-math.rkc-74.ru%2FDswMedia%2Fprez.ppt&ei=ZMTtTu3DK6n04QSeydzvCA&usg=AFQjCNHLpVSYyHE9W7QxccbJCuuAOl4JYQ Вопрос Пасаны, найдите и киньте в группу пожалуйсто) 17 вопрос Вопрос No))) Вопрос 1.Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. 2.Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй. 3.Произведение суммы двух величин на их разность равно разности их квадратов. 4.Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй. 5.Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй. 7. Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 +
+  n, где n
n, где n 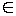 Z и x = (-1)n
Z и x = (-1)n  +
+ 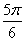 .
.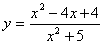 .
. 1, то квадратное уравнение, которое мы получили в результате выше изложенных соображений, имеет корни тогда и только тогда, когда его дискриминант не отрицателен.
1, то квадратное уравнение, которое мы получили в результате выше изложенных соображений, имеет корни тогда и только тогда, когда его дискриминант не отрицателен. 0;
0; и y = 2 +
и y = 2 +  .
. 0; Откуда х = 5. Таким образом область определения данной функции состоит из одного числа, следовательно, множество значений функции состоит из одного числа и Е(у) = {11}.
0; Откуда х = 5. Таким образом область определения данной функции состоит из одного числа, следовательно, множество значений функции состоит из одного числа и Е(у) = {11}.



