
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип возможных перемещений при равновесии материальной системы. Общее уравнение статики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть материальная система находится в равновесии. Силы, действующие на каждую ее точку, уравновешиваются. Если
Рис.65
Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения Затем вычислим работу всех сил на этих перемещениях. Так как силы, приложенные к каждой точке уравновешиваются и
Если связи идеальные, то вторая сумма всегда равна нулю. Значит,
Этот результат, уравнение работ, называют общим уравнением статики. При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю. Конечно, если у системы есть неидеальные связи, например, с трением, или упругие, вроде пружины, то в уравнение работ надо добавить возможную работу реакций этих связей. Принцип возможных перемещений можно записать в другой форме. Если возможные перемещения точек определить с помощью возможных скоростей:
где Равенство (2) можно назвать принципом возможных скоростей, уравнением мощностей. Оно иногда бывает более удобным, так как используются конечные величины скоростей, а не бесконечно малые перемещения. Этот принцип, общее уравнение статики, позволяет решать задачи на исследование равновесного состояния системы, в частности – находить неизвестные реакции связей. Естественно, при этом возникает вопрос: как же так, ведь реакции идеальных связей не входят в уравнение работ? Выход прост – надо сделать тело свободным, реакции отнести к разряду активных сил и затем назначать такие возможные перемещения, чтобы эти неизвестные силы совершали работу. Общее уравнение статики – довольно эффективный метод и применять его, конечно, надо для исследования равновесия сложных систем; хотя и при решении обычных задач статики он оказывается тоже выгодным.
Уравнения Лагранжа. По определению (7) и (12) обобщенные силы
Сумма их
Но на основании общего уравнения динамика (3), правая часть равенства равна нулю. И так как все
Эти уравнения называются дифференциальными уравнениями движения в обобщенных координатах, уравнениями Лагранжа второго рода или просто – уравнениями Лагранжа. Количество этих уравнений равно числу степеней свободы материальной системы. Если система консервативная и движется под действием сил потенциального поля, когда обобщенные силы
или где L = T – П называется функцией Лагранжа (предполагается, что потенциальная энергия П не зависит от обобщенных скоростей). Нередко при исследовании движения материальных систем оказывается, что некоторые обобщенные координаты qj не входят явно в функцию Лагранжа (или в Т и П). Такие координаты называют циклическими. Уравнения Лагранжа, соответствующие этим координатам, получаются проще. Так как Первый интеграл таких уравнений находится сразу. Он называется циклическим интегралом:
Дальнейшие исследования и преобразования уравнений Лагранжа составляют предмет специального раздела теоретической механики – «Аналитическая механика». Уравнения Лагранжа обладают целым рядом достоинств в сравнении с другими способами исследования движения систем. Основные достоинства: методика составления уравнений одинакова во всех задачах, реакции идеальных связей не учитываются при решении задач. И еще одно – эти уравнения можно использовать для исследования не только механических, но и других физических систем (электрических, электромагнитных, оптических и др.).
Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное Иваном Мещерским в 1904 году. Оно имеет вид:
где: § m — переменная масса тела; § v — скорость движения тела переменной массы; § F — внешние силы (сопротивление среды и т. п.); § § § §
Реактивная тяга — сила, возникающая в результате взаимодействия двигательной установки с истекающей из сопла камеры сгорания струей расширяющихся продуктов сгорания, обладающих кинетической энергией.[1] Природа возникновения реактивной тяги заключена в физико-химических процессах протекающих в двигательной установке при сгорании топлива. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения - центр среза сопла двигателя, а направление - противоположноевектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга: § приложена непосредственно к корпусу реактивного двигателя; § обеспечивает передвижение ракетного двигателя и связанного с ним аппарата в сторону, противоположную направлению реактивной струи.[2]
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

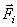 – равнодействующая всех активных сил, приложенных к i -той точке, а
– равнодействующая всех активных сил, приложенных к i -той точке, а  – реакция связей этой точки, то (рис.65)
– реакция связей этой точки, то (рис.65)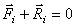

 ,
,  ,
,  ,…,
,…,  .
.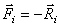 , то сумма работ этих сил на перемещении
, то сумма работ этих сил на перемещении 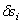 будет равна нулю:
будет равна нулю: 
 . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю
. Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю .
.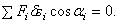 (1)
(1) где время
где время  - произвольная бесконечно малая величина, то уравнение работ (1) запишется так
- произвольная бесконечно малая величина, то уравнение работ (1) запишется так 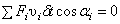 , а, поделив его на
, а, поделив его на  , (2)
, (2) – углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.
– углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.
 .
. или
или .
. (k = 1,2,3,…, s) отличны от нуля, то
(k = 1,2,3,…, s) отличны от нуля, то 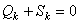 . Подставив значение обобщенной силы инерции (17), получим уравнение
. Подставив значение обобщенной силы инерции (17), получим уравнение (k = 1,2,3,…, s). (18)
(k = 1,2,3,…, s). (18) , уравнения Лагранжа можно составить по форме
, уравнения Лагранжа можно составить по форме (19)
(19) (k = 1,2,3,…, s), (20)
(k = 1,2,3,…, s), (20) и
и 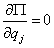 , то
, то 
 (21)
(21) ,
, — относительная скорость отделяющихся частиц;
— относительная скорость отделяющихся частиц; — относительная скорость присоединяющихся частиц;
— относительная скорость присоединяющихся частиц;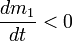 — секундный расход массы;
— секундный расход массы; — секундный приход массы.
— секундный приход массы.


