
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия относительного покоя. Сила тяжестиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть материальная точка под действием приложенных к ней сил находится в состоянии относительного покоя, т.е. не движется относительно подвижной системы отсчета Oxyz. В этом случае относительная скорость Таким образом, если материальная точка находится в состоянии относительного покоя, геометрическая сумма действующих на нее сил и переносной силы инерции равна нулю. Следует отметить, что выполнения условия (3.8) не означает, что после сообщения точке начальной скорости она будет двигаться равномерно и прямолинейно относительно подвижной системы, как это имеет место в инерциальной системе отсчета. Действительно, при появлении относительной скорости, во-первых, возникает кориолисово ускорение Рассмотрим в качестве примера материальную точку М, подвешенную на нити и находящуюся в покое относительно Земли (рис. 3.3). Запишем условие относительного покоя (3.8) и получим где
где ρ = МК – радиус географической параллели; R – радиус Земли; ω – угловая скорость вращения Земли; φ – геоцентрическая широта. Силу, равную по модулю и направленную противоположно реакции Направление силы тяжести Сила инерции
Оно максимально на экваторе (1/290) и равно нулю на полюсе. Отклонение линии отвеса от направления радиуса Земли максимально на широте 450 и составляет
Масса системы. Центр масс. Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему
В однородном поле тяжести, для которого
В полученные равенства входят только массы Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы. Положение центра масс определяется его радиус-вектором
где Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.117.147 (0.011 с.) |

 и относительное ускорение
и относительное ускорение 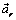 точки равны нулю, следовательно, равна нулю и кориолисова сила инерции
точки равны нулю, следовательно, равна нулю и кориолисова сила инерции 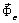 . Уравнение относительного покоя получим из уравнения (3.5)
. Уравнение относительного покоя получим из уравнения (3.5)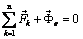 . (3.8)
. (3.8)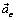 и кориолисова сила инерции
и кориолисова сила инерции 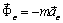 , во-вторых, может измениться переносное ускорение, зависящее от положения точки в подвижной системе отсчета, что приведет к изменению переносной силы инерции
, во-вторых, может измениться переносное ускорение, зависящее от положения точки в подвижной системе отсчета, что приведет к изменению переносной силы инерции 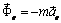 . Таким образом, правая часть уравнения (3.5) будет отлична от нуля, и точка будет иметь относительное ускорение
. Таким образом, правая часть уравнения (3.5) будет отлична от нуля, и точка будет иметь относительное ускорение 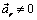 .
.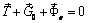 , (3.9)
, (3.9)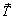 – реакция нити;
– реакция нити;  – сила притяжения Земли, направленная к ее центру;
– сила притяжения Земли, направленная к ее центру; 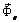 – переносная сила инерции, которая вследствие равномерного вращения Земли имеет только центробежную составляющую, направленную от ее оси вращения. Модуль силы инерции
– переносная сила инерции, которая вследствие равномерного вращения Земли имеет только центробежную составляющую, направленную от ее оси вращения. Модуль силы инерции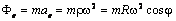 ,
,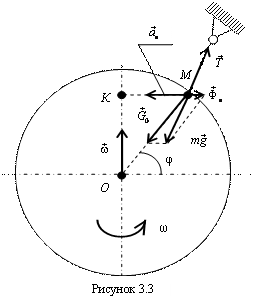
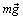 . Таким образом, сила тяжести равна геометрической сумме силы притяжения
. Таким образом, сила тяжести равна геометрической сумме силы притяжения 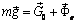 .
.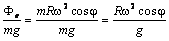 .
.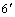 . Таким образом, сила тяжести
. Таким образом, сила тяжести 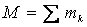 .
.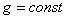 , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:
, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести: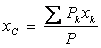 ,
, 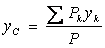 ,
,  . (1)
. (1)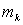 материальных точек (частиц), образующих тело, и координаты
материальных точек (частиц), образующих тело, и координаты 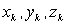 этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под
этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под 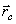
 ,
,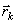 -радиус-векторы точек, образующих систему.
-радиус-векторы точек, образующих систему.


