
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия системы. Закон Кёнига.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач. Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
Кинетическая энергия – скалярная и всегда положительная величина. Найдем формулы для вычисления кинетической энергии тела в разных случаях движения. 1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки
или
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит. 2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
Рис.46
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)
или, окончательно,
где Ix, Iy, Iz – моменты инерции тела относительно главных осей инерции x 1, y 1, z 1 в неподвижной точке О;
Рис.47
3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис.46). Следовательно
где
Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной скинетической энергией вращательного движения вокруг центра масс. 4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига. Рассмотрим движение материальной системы как сумму двух движений (рис.48). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x 1, y 1, z 1. Тогда скорость точек
Рис.48
По определению центра масс его радиус-вектор в подвижной системе
Поэтому, окончательно, кинетическая энергия системы
Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс. В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим
где Ix, Iy, Iz – главные центральные оси инерции тела. 52. Работа силы…
Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.
Рис.16
При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки. Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы
где Данное определение соответствует понятию о работе, как о характеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу Замечая, что
Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементарное перемещение Если угол Если угол Если угол Найдем аналитическое выражение элементарной работы. Для этого разложим силу
Рис.17
Элементарное перемещение Но на перемещении Формула дает аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М 0 М 1 вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:
Следовательно, работа силы на любом перемещении М 0 М 1 равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям переменных интегрирования в точках М 0 и М 1.
Рис.18 Если величина Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F = const), а точка, к которой приложена сила, движется прямолинейно (рис.18}. В этом случае Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).
Работа силы упругости при одномерном растяжении (или сжатии), характеризующемся вектором удлинения (сжатия), Если одна из координатных осей (например, Ох) выбранной системы отсчета совпадает по направлению, с вектором, то где x1 и x2 — координаты начала и конца вектора. При перемещении точки упруго деформируемого тела по замкнутой траектории работа силы упругости равна нулю (Аупр = 0 при =0 или при x1 = x2).
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |





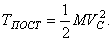
 , где
, где 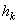 - расстояние точки от оси вращения, а w- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
- расстояние точки от оси вращения, а w- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:



 ,
, ,
, 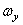 ,
,  – проекции вектора мгновенной угловой скорости
– проекции вектора мгновенной угловой скорости  на эти оси.
на эти оси.
 ,
,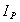 - момент инерции тела относительно названной выше оси, w- угловая скорость тела. Величина
- момент инерции тела относительно названной выше оси, w- угловая скорость тела. Величина  , относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса
, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса  , где d=PC. Подставим это выражение для
, где d=PC. Подставим это выражение для  , где
, где  - скорость центра масс С, окончательно найдем:
- скорость центра масс С, окончательно найдем: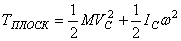 .
.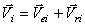 . Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны
. Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны  . Значит,
. Значит,  и кинетическая энергия будет
и кинетическая энергия будет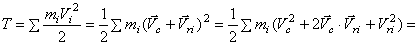
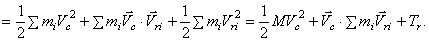

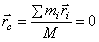 (центр масс находится в начале координат), значит, и
(центр масс находится в начале координат), значит, и  . Производная по времени от этой суммы также равна нулю:
. Производная по времени от этой суммы также равна нулю: .
. (1)
(1) или
или  ,
,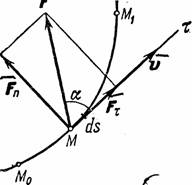
 (рис.16) называется скалярная величина:
(рис.16) называется скалярная величина: ,
,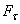 - проекция силы
- проекция силы  -бесконечно малое перемещение точки, направленное вдоль этой касательной.
-бесконечно малое перемещение точки, направленное вдоль этой касательной. и
и  , то изменять модуль скорости точки будет только составляющая
, то изменять модуль скорости точки будет только составляющая 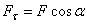 , получаем:
, получаем: . (1)
. (1) острый, то работа положительна. В частности, при
острый, то работа положительна. В частности, при  элементарная работа
элементарная работа  .
. элементарная работа
элементарная работа 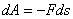 .
. , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.
, т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю. ,
,  ,
,  по направлениям координатных осей (рис.17; сама сила
по направлениям координатных осей (рис.17; сама сила 
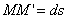 слагается из перемещений
слагается из перемещений  ,
, 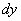 ,
,  вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы
вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы  . Работа на перемещениях
. Работа на перемещениях  .
.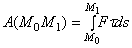
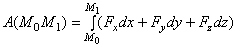 .
.
 получим:
получим: 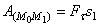 .
. и работа силы
и работа силы  .
.


