
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярно-кинетическая теория идеальных газовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
· Концентрация частиц (молекул, атомов и т.п.) однородной системы
где V -объём системы · Основное уравнение кинетической теории газов
где p — давление газа; < Ek >-средняя кинетическая энергия поступательного движения молекулы. · Средняя кинетическая энергия: приходящаяся на одну степень свободы молекулы
приходящаяся на все степени свободы молекулы (полная энергия молекулы)
поступательное движение молекулы
где k -постоянная Больцмана; T- термодинамическая температура; i- число степеней свободы молекулы; Энергия вращательного движения молекулы
· Зависимость давления газа от концентрации молекул и температуры
· Скорость молекулы: средняя квадратичная
средняя арифметическая
наиболее вероятная
где m 1 – масса одной молекулы. · Барометрическая формула
где ph и p 0 – давление газа на высоте h и h 0. · Распределение Больцмана во внешнем потенциальном поле
где n и n 0 – концентрация молекул на высоте h и h =0; П= m 0 gh – потенциальная энергия молекулы в поле тяготения. · Среднее число соударений, испытываемых молекулой газа за 1 с где d – эффективный диаметр молекулы; n – концентрация молекул; <υ> - средняя арифметическая скорость молекул. · Средняя длина свободного пробега молекул газа
· Закон теплопроводности Фурье
где Q – теплота, прошедшая посредством теплопроводности через площадь S за время t; dT / dx – градиент температуры; λ – теплопроводность:
где cV – удельная теплоемкость газа при постоянном объеме; ρ – плотность газа; <υ> - средняя арифметическая скорость теплового движения его молекул; < l > - средняя длина свободного пробега молекул. · Закон диффузии Фика
где M – масса вещества, переносимая посредством диффузии через площадь S за время t; d ρ/ dx – градиент плотности; D – диффузия:
· Закон Ньютона для внутреннего трения (вязкости)
где F – сила внутреннего трения между движущимися слоями площадью S; dυ/dx – градиент скорости; η – динамическая вязкость:
6.1. Начертить графики изотермического, изобарного и изохорного процессов в координатах P и V, P и Т, Т и V. 6.2. Определить число N атомов в 1 кг водорода и массу одного атома водорода. Ответ: Н = 3,01·1026; т0 = 3,32.10-27 кг. 6.3. В закрытом сосуде вместимостью 20 л находятся водород массой 6 г и гелий массой 12 г. Определить: 1) давление; 2) молярную массу газовой смеси в сосуде, если температура смеси Т = 300 К. Ответ: 1) P = 0,75 кПа; 2) М = 3·10-3 кг/моль. 6.4. Определить плотность смеси газов водорода массой m1 = 8 г и кислорода массой m2 = 64 г при температуре Т = 290 К и при давлении 0,1 МПа. Газы считать идеальными. Ответ: 0,498 кг/м3. 6.5. Баллон вместимостью V = 20 л содержит смесь водорода и азота при температуре 290 К и давлении 1 МПа. Определить массу водорода, если масса смеси равна 150 г. Ответ: 6,3 г. 6.6. В сосуде вместимостью 1 л находится кислород массой 1 г. Определить концентрацию молекул кислорода в сосуде. Ответ: 1,88.1025 м-3. 6.7. Определить наиболее вероятную скорость молекул газа, плотность которого при давлении 40 кПа составляет 0,35 кг/м3. Ответ: 478 м/с. 6.8. Определить среднюю кинетическую энергию <E 0 > поступательного движения молекул газа, находящегося под давлением 0,1 Па. Концентрация молекул газа равна 1013 см-3. Ответ: 1,5·10-19 Дж. 6.9. Используя закон распределения молекул идеального газа по скоростям, найти формулу наиболее вероятной скорости υB. Ответ: υB = 6.10. Используя закон распределения молекул идеального газа по скоростям, найти закон, выражающий распределение молекул по относительным скоростям и (u = υ/υв). Ответ: f (u) = 6.11. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать, что температура воздуха везде одинакова и равна 10 °С. Ответ: 4,22 км. 6.12. Каково давление воздуха в шахте на глубине 1 км, если считать, что температура по всей высоте постоянная и равна 22 °С, а ускорение свободного падения не зависит от высоты. Давление воздуха у поверхности Земли принять равным P0. Ответ: 1,12 P0. 6.13. Определить отношение давления воздуха на высоте 1 км к давлению на дне скважины глубиной 1 км. Воздух у поверхности Земли находится при нормальных условиях, и его температура не зависит от высоты Ответ: 0,78. 6.14. На какой высоте плотность воздуха в е раз (е — основание натуральных логарифмов) меньше по сравнению с его плотностью на уровне моря? Температуру воздуха и ускорение свободного падения считать не зависящими от высоты. Ответ: 7,98 км. 6.15. Определить среднюю длину свободного пробега < l > молекул кислорода, находящегося при температуре 0 °С, если среднее число < z > столкнрвений, испытываемых молекулой в 1 с, равно 3,7·109. Ответ: 115 нм. 6.16. При каком давлении средняя длина свободного пробега молекул водорода равна 2,5 см, если температура газа равна 67 °С? Диаметр молекулы водорода принять равным 0,28 нм. Ответ: 0,539 Па. 6.17. Определить среднюю продолжительность <τ> свободного пробега молекул водорода при температуре 27 °С и давлении 5 кПа. Диаметр молекулы водорода' принять равным 0,28 нм. Ответ: 13,3 нс. 6.18. Средняя длина свободного пробега < l > молекул водорода при нормальных условиях составляет 0,1 мкм. Определить среднюю длину их свободного пробега при давлении 0,1 мПа, если температура газа остается постоянной. Ответ: 101 м. 6.19. При температуре 300 К и некотором давлении средняя длина свободного пробега < l > молекул кислорода равна 0,1 мкм. Чему равно среднее число < z > столкновений, испытываемых молекулами в 1 с, если сосуд откачать до 0,1 первоначального давления? Температуру газа считать постоянной. Ответ: 4,45.108 с-1. 6.20. Определить коэффициент теплопроводности λ азота, находящегося в некотором объеме при температуре 280 К. Эффективный диаметр молекул азота принять равным 0,38 нм. Ответ: 8,25 мВт/(м.К). 6.21. Кислород находится при нормальных условиях. Определить коэффициент теплопроводности λ кислорода, если эффективный диаметр его молекул равен 0,36 нм. Ответ: 8,49 мВт/(м·К). 6.22. Пространство между двумя параллельными пластинами площадью 150 см2 каждая, находящимися на расстоянии 5 мм друг от друга, заполнено кислородом. Одна пластина поддерживается при температуре 17 °С, другая – при температуре 27 °С. Определить количество теплоты, прошедшее за 5 мин посредством теплопроводности от одной пластины к другой. Кислород находится при нормальных условиях. Эффективный диаметр молекул кислорода считать равным 0,36 нм. Ответ: 76,4 Дж. 6.23. Определить коэффициент диффузии D кислорода при нормальных условиях. Эффективный диаметр молекул кислорода принять равным 0,36 нм. Ответ: 9,18.10-6 м2/с. 6.24. Определить массу азота прошедшего вследствие диффузии через площадку 50 см2 за 20 с, если градиент плотности в направлении, перпендикулярном площадке, равен 1 кг/м4. Температура азота 290 К, а средняя длина свободного пробега его молекул равна 1 мкм. Ответ: 15,6 мг. 6.25. Определить коэффициент теплопроводности λ азота, если коэффициент динамической вязкости η для него при тех же условиях равен 10 мкПа.с Ответ: 7,42 мВт/(м.К).
Основы термодинамики
· Связь между молярной (Cm) и удельной (c) теплоёмкостями газа
где M -молярная масса газа. · Молярные теплоёмкости * при постоянном объёме и постоянном давлении соответственно равны
где i- число степеней свободы; R- молярная газовая постоянная. · Удельные теплоемкостью при постоянном объёме и постоянном давлении соответственно равны
· Уравнение Майера · Показатель адиабаты
· Внутренняя энергия идеального газа
где < Ek >-средняя кинетическая энергия молекулы; N- число молекул газа; k- количество вещества, · Работа, связанная с изменением объёма газа, в общем случае вычисляется по формуле
где – V1 начальный объём газа; V2 - его конечныё объём. Работа газа; а) при изобарном процессе (p=const)
б) при изотермическом процессе (T=const)
в) при адиабатном процессе
где T1 – начальная температура газа; T2 – ого конечная температура.
· Уравнение Пуассона (уравнение газового состояния при адиабатном процессе)
· Связь между начальным и конечным значениями параметров состояния газа при адиабатном процессе:
· Первое начало термодинамики в общем случае записывается в виде
где Q -количество теплоты, сообщение газу; ∆ U -изменение его внутренней энергии; A -работа, совершаемая газом против внешних сил. Первое начало термодинамики: а) при изобарном процессе
б) при изохорном процессе (A=0)
в) при изотермическом процессе (∆U=0)
г) при адиабатном процессе (Q=0)
· Термический коэффициент полезного действия (КПД) цикла в общем случае
где Q1 – количество теплоты, полученное рабочим телом (газом) от нагревателя; Q2 – количество теплоты, переданное рабочим телом охладителю. КПД цикла Карно
где T1 – температура нагревателя; T1 – температура охладителя. · Изменение энтропии
где А и В – пределы интегрирования, соответствующие начальному и конечному состоянию системы. Так как процесс равновесный, то интегрирование проводится по любому пути. · Формула Больцмана
где S – энтропия системы; W – термодинамическая вероятность её состояния; k – постоянная Больцмана. 7.1. Азот массой m = 10 г находится при температуре Т = 290 К. Определить: 1) среднюю кинетическую энергию одной молекулы азота; 2) среднюю кинетическую энергию вращательного движения всех молекул азота. Газ считать идеальным. Ответ: 1) 10-20 Дж; 2) 860 Дж. 7.2. Кислород массой m = 1 кг находится при температуре Т = 320 К. Определить: 1) внутреннюю энергию молекул кислорода; 2) среднюю кинетическую энергию вращательного движения молекул кислорода. Газ считать идеальным. Ответ: 1) 208 кДж; 2) 83,1 кДж. 7.3. В закрытом сосуде находится смесь азота массой m 1 = 56 г и кислорода массой m 2 = 64 г. Определить изменение внутренней энергии этой смеси, если ее охладили на 20°. Ответ: 1,66 кДж. 7.4. Считая азот идеальным газом, определить его удельную теплоемкость: 1) для изобарного процесса; 2) для изохорного процесса. Ответ: 1) cV = 742 Дж/(кг.К); 2) cр = 1,04 кДж/(кг.К). 7.5. Определить удельные теплоемкости cV и cр, если известно, что некоторый газ при нормальных условиях имеет удельный объем V = 0,7 м3/кг. Что это за газ? Ответ: cV = 649 Дж/(кг·К), ср = 909 Дж/(кг·К). 7.6. Определить удельные теплоемкости cv и ср смеси углекислого газа массой m 1 = 3 г и азота массой m2 = 4 г. Ответ: cV = 667 Дж/(кг.К), сp = 918 Дж/(кг.К). 7.7. Определить показатель адиабаты г для смеси газов, содержащей гелий массой m1 = 8 г и водород массой m2 = 2 г Ответ: 1,55. 7.8. Применяя первое начало термодинамики и уравнение состояния идеального газа, показать, что разность удельных теплоемкостей ср – cV = R/M. 7.9. Кислород массой 32 г находится в закрытом сосуде под давлением 0,1 МПа при температуре 290 К. После нагревания давление в сосуде повысилось в 4 раза. Определить: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу. Ответ: 1) 2,4.10-2 м3; 2) 1,16 кК; 3) 18,1 кДж. 7.10. Определить количество теплоты, собщенное газу, если в процессе изохорного нагревания кислорода объемом V = 20 л его давление изменилось на Δ P = 100 кПа. Ответ: 5 кДж. 7.11. Двухатомный идеальный газ (ν = 2 моль) нагревают при постоянном объеме до температуры T 1 = 289 К. Определить количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в n = 3 раза. Ответ: 24 кДж. 7.12. При изобарном нагревании некоторого идеального газа (ν = 2 моль) на Δ T = 90 К ему было сообщено количество теплоты 2,1 кДж. Определить: 1) работу, совершаемую газом; 2) изменение внутренней энергии газа; 3) величину γ = Cp / CV. Ответ: 1) 1,5кДж; 2) 0,6 кДж; 3) 1,4. 7.13. Азот массой m = 280 г расширяется в результате изобарного процесса при давлении P = 1 МПа. Определить: 1) работу расширения; 2) конечный объем газа, если на расширение затрачена теплота Q = 5 кДж, а начальная температура азота T 1 = 290 К. Ответ: А = 1,43 кДж; V2= 0,026 м3. 7.14. Кислород объемом 1 л находится под давлением 1 МПа. Определить, какое количество теплоты необходимо сообщить газу, чтобы: 1) увеличить его объем вдвое в результате изобарного процесса; 2) увеличить его давление вдвое в результате изохорного процесса. Ответ: 1) 3,5 кДж; 2) 2,5 кДж. 7.15. Некоторый газ массой m = 5 г расширяется изотермически от объема V1 до объема V2 = 2 V1. Работа расширения А = 1 кДж. Определить среднюю квадратичную скорость молекул газа. Ответ: 930 м/с. 7.16. Азот массой m = 14 г сжимают изотермически при температуре Т = 300 К от давления P 1 = 100 кПа до давления P 2 = 500 кПа. Определить: 1) изменение внутренней энергии газа; 2) работу сжатия; 3) количество выделившейся теплоты. Ответ: 1) 0; 2) –2,01 кДж; 3) 2,01 кДж. 7.17. Некоторый газ массой 1 кг находится при температуре Т = 300 К и под давлением P 1 = 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в два раза. Работа, затраченная на сжатие, А = –432 кДж. Определить: 1) какой это газ; 2) первоначальный удельный объем газа. Ответ: 2) 1,25 м3/кг. 7.18. Азот массой m = 50 г находится при температуре T 1= 280 К. В результате изохорного охлаждения его давление уменьшилось в n = 2 раза, а затем в результате изобарного расширения температура газа в конечном состоянии стала равной первоначальной. Определить: 1) работу, совершенную газом; 2) изменение внутренней энергии газа. Ответ: 1) 2,08 кДж; 2) 0. 7.19. Работа расширения некоторого двухатомного идеального газа составляет А = 2 кДж. Определить количество подведенной к газу теплоты, если процесс протекал: 1) изотермически; 2) изобарно. Ответ: 1) 3 кДж; 2) 7 кДж. 7.20. При адиабатическом расширении кислорода (ν = 2 моль), находящегося при нормальных условиях, его объем увеличился в n = 3 раза. Определить: 1) изменение внутренней энергии газа; 2) работу расширения газа. Ответ: 1) –4,03 кДж; 2) 4,03 кДж. 7.21. Азот массой m = 1 кг занимает при температуре T1 = 300 К объем V1 = 0,5 м3. В результате адиабатического сжатия давление газа увеличилось в 3 раза. Определить: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа. Ответ: 1) 0,228 м3; 2) 411 К; 3) 82,4 кДж. 7.22. Азот, находившийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объем увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определить массу азота. Ответ: 28 г. 7.23. Двухатомный идеальный газ занимает объем V 1 = 1 л и находится под давлением P 1 = 0,1 МПа. После адиабатического сжатия газ характеризуется объемом V 2 и давлением P 2. В результате последующего изохор-ного процесса газ охлаждается до первоначальной температуры, а его давление P 3 = 0,2 МПа. Определить: 1) объем V 2; 2) давление P 2. Начертить график этих процессов. Ответ: 1) 0,5л; 2) 264 кПа. 7.24. Кислород, занимающий при давлении P 1 = 1 МПа объем V 1= 5 л, расширяется в n = 3 раза. Определить конечное давление и работу, совершенную газом. Рассмотреть следующие процессы: 1) изобарный; 2) изотермический; 3) адиабатический. Ответ: 1) 1 МПа, 10 кДж; 2) 0,33 МПа, 5,5 кДж; 3) 0,21 МПа, 4,63 кДж. 7.25. Рабочее тело – идеальный газ – теплового двигателя совершает цикл, состоящий из последующих процессов: изобарного, адиабатического и изотермического. 7.26. В результате изобарного процесса газ нагревается от T 1 = 300 К до Т 2 = 600 К. Определить термический к.п.д. теплового двигателя. Ответ: 30,7 %. 7.27. Азот массой 500 г, находящийся под давлением P 1 = 1 МПа при температуре T 1= 127 °С, подвергли изотермическому расширению, в результате которого давление газа уменьшилось в n = 3 раза. После этого газ подвергли адиабатическому сжатию до начального давления, а затем он был изобарно сжат до начального объема. Построить график цикла и определить работу, совершенную газом за цикл. Ответ: –11,5 кДж. 7.28. Идеальный газ, совершающий цикл Карно, 70 % количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) термический к.п.д. цикла; 2) работу, совершенную при полном цикле. Ответ: 1) 30%; 2) 1,5 кДж. 7.29. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический к.п.д. цикла; 2) отношение температур нагревателя и холодильника. Ответ: 1) 20%; 2) 1,25. 7.30. Идеальный газ совершает цикл Карно, термический к.п.д. которого равен 0,4. Определить работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж. Ответ: –240 Дж. 7.31. Идеальный газ совершает цикл Карно. Температура нагревателя Т 1 = 500 К, холодильника Т 2 = 300 К. Работа изотермического расширения газа составляет 2 кДж. Определить: 1) термический к.п.д. цикла; 2) количество теплоты, отданное газом при изотермическом сжатии холодильнику. Ответ: 1) 40 %; 2) 0,6 кДж. 7.32. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатического расширения объем газа увеличивается в n = 4 раза. Определить термический к.п.д. цикла. Ответ: 37 %. 7.33. Во сколько раз необходимо увеличить объем V = 5 моль идеального газа при изотермическом расширении, если его энтропия увеличилась на 57,6 Дж/К? Ответ: 4. 7.34. При нагревании двухатомного идеального газа (ν = 3 моль) его термодинамическая температура увеличилась в n = 2 раза. Определить изменение энтропии, если нагревание происходит: 1) изохорно; 2) изобарно. Ответ: 1) 28,8 Дж/К; 2) 40,3 Дж/К. 7.35. Идеальный газ (ν = 2 моль) сначала изобарно нагрели, так что объем газа увеличился в n 1 = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n = 2 раза. Определить приращение энтропии в ходе указанных процессов. Ответ: 11,5 Дж/К. 7.36. Азот массой 28 г адиабатически расширили в n = 2 раза, а затем изобарно сжали до первоначального объема. Определить изменение энтропии газа в ходе указанных процессов. Ответ: –0,2 Дж/К.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 804; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.009 с.) |

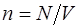
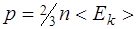



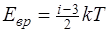

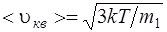 , или
, или 
 , или
, или 
 , или
, или 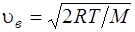


 ,
,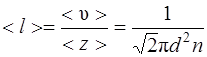 .
. ,
,
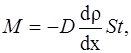
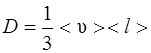 .
. ,
, .
.
 .
.
 ;
; 
 ;
; 
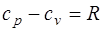
 , или
, или  , или
, или  .
. , или
, или  ,
, .
.



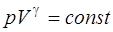
 ;
; 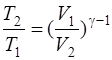 ;
; 





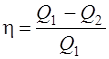

 ,
, ,
,


