Экспериментальные газовые законы

Лабораторная работа №46.

«Экспериментальные газовые законы»

Составитель: О. В. Сергеева, к.ф.-м.н., доцент

Рецензент: И. А. Малиненко, к.ф.-м.н., доцент

Цели работы:

1. Изучить понятие идеального газа.

2. Изучить экспериментальные газовые законы для идеального газа.

3. Изучить уравнение состояния идеального газа.

Задачи:

1. Проверить, является ли воздух, находящийся при атмосферном давлении и комнатной температуре идеальным газом.

2. Проверить выполнение экспериментальных газовых законов для воздуха.

3. Рассчитать универсальную газовую постоянную различными способами.

4. Рассчитать и сравнить между собой термические коэффициенты объемного расширения и давления для воздуха.

Приборы и принадлежности

1. Универсальная установка Кобра 3.

2. Источник питания на 12 В.

3. Датчик давления.

4. Программное обеспечение для изучения уравнения состояния газа.

5. Полупроводниковый датчик, -10..120 °C.

6. Стеклянный корпус.

7. Газовый шприц на 100 мл.

8. Нагреватель.

9. H-образная опора.

10. Магнит, магнитная мешалка.

11. Трубка-переходник для подключения датчика давления.

Идеальный газ

Системы, состоящие из большого числа молекул, называются макросистемами. К таким системам относятся, например, газ, жидкость, жидкие кристаллы, твердые тела, плазма.

Теоретическое изучение макросистем связано с большими трудностями, так как для этого требуется учесть все силы, которые действуют на каждую молекулу со стороны всех других. Если предположить, что движения молекул являются чисто механическими и подчиняются законам механики, то для полного описания всякой молекулярной системы нужно решить механическую задачу о движении всех молекул под действием заданных сил. Это значит, что должны быть написаны и решены уравнения движения, число которых равно числу молекул в данной системе (точнее говоря, число уравнений должно быть втрое больше, поскольку положение молекулы определяется тремя координатами, поскольку каждая молекула имеет три степени свободы). Если учесть, что, например, в 1 см³ газа при обычных условиях содержится 2,7 ^. 10¹⁹ молекул, то ясно, что не только решить, но даже написать такое число уравнений невозможно.

Но именно большое количество молекул делает ненужным рассмотрение движения каждой из них в отдельности. При таком большом числе частиц оказывается возможным ограничиться знанием лишь средних значений величин, характеризующих их движение: их средней скорости, средней энергии и т. д. Этим приемом и пользуются в молекулярно-кинетическом подходе при изучении молекулярных систем.

Из трех агрегатных состояний, в которых может находиться всякое вещество, наиболее простым является газообразное, так как в этом случае силы, действующие между молекулами, очень малы и ими при определенных условиях можно пренебречь. Будем считать, что межмолекулярные силы в них даже не малы, а полностью отсутствуют. Пренебрежем также размерами молекул, будем считать их материальными точками. При таких допущениях молекулы газа должны считаться совершенно свободными. Этозначит, что движутся они прямолинейно и равномерно, как всегда движутся тела, не подверженные действию каких-либо сил. Каждая молекула ведет себя, следовательно, так, как будто других молекул в сосуде нет. Газ, обладающий такими же свойствами, как и совокупность невзаимодействующих материальных точек, называется идеальным газом.

Таким образом, идеальный газ удовлетворяет следующим условиям:

1. Между молекулами газа отсутствуют силы взаимодействия на расстоянии;

2. Объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, т. е. молекулы газа можно считать материальными точками;

3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Идеальный газ – это модель, применяемая для описания реальных газов. Любой газ, находящийся в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах, близки по своим свойствам к идеальному.

Ученые используют модель идеального газа даже в сложных теоретических расчетах. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. Интересно, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. Дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия, то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов. Понятие «идеальный газ» используют также для описания свойств совокупности частиц различной природы: фотоны, электроны, фононы и т. д.

Закон Гей-Люссака

Пусть теперь газ находится в условиях, когда постоянным сохраняется его давление р и масса,но изменяется температура. Такие условия можно осуществить, если поместить газ в цилиндр, закрытый легким подвижным поршнем. В таком цилиндре изменение температуры вызывает перемещение поршня и изменение объема, давление же остается постоянным. Для данной массы газа при постоянном давлении р = const объем газа изменяется линейно с температурой (закон Гей-Люссака):

(2),

где V_o – объем газа при 0^oС, V – объем газа при температуре t, a_p –термический коэффициент объемного расширения газа при постоянном давлении (или изобарический коэффициент объемного расширения газа, или изобарный коэффициент давления).

Уравнение (2), называемое уравнением изобары (процесс, происходящий при постоянном давлении, называется изобарическим), выражает закон Ж. Л. Гей-Люссака. Этот закон был открыт им в 1802 году.

Коэффициент объемного расширения a для любых вещество определяют как:

(3)

Индекс pу производной показывает, что она берется при p = const Для идеального газа в соответствии с выражением (2) он будет равен

(4)

Коэффициент объемного расширения представляет собой относительное изменение объема при изменении температуры на 1 К при изобарическом процессе. Относительное изменение объема определяется по отношению к объему, занимаемому газом при 0^оС.

Закон Шарля

Для данной массы газа при постоянном объеме V = const давление газа изменяется линейно с температурой (закон Шарля):

(5)

где р_о – давление газа при 0^оС, р – давление газа при температуре t, a_V – термический коэффициент давления газа для изохорического процесса (или изохорный коэффициент давления, или термический коэффициент давления).

Уравнение (5), называемое уравнением изохоры (процесс, происходящий при постоянном объеме, называется изохорическим), выражает закон Шарля. Этот закон был открыт им в 1787 году.

Термический коэффициент давления любого вещества для изохорического процесса определяют как

(6).

Индекс Vу производной показывает, что она берется при V = const. Для идеального газа в соответствии с выражением (5) этот коэффициент будет равен

(7)

Термический коэффициент объемного расширения представляет собой относительное изменение давления при изменении температуры на 1 К при изохорическом процессе. Относительное изменение давления определяется по отношению к давлению, соответствующему нормальным условиям, то есть при 0^оС.

Экспериментально установлено, что для идеального газа

(8).

Согласно формулам (2) и (5), изобарический и изохорический процессы представляются на графиках прямыми линиями (изобарами и изохорами) (рис. 2, 3), проходящими наклонно к оси температур и пересекающими ее в точке , определяемой из условия 1 + at = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (рис. 2, 3), откуда Т = t + . Точка принята за начало отсчета новой шкалы температур, называемой термодинамической шкалой (шкалой Кельвина), или абсолютной шкалой. Температура, отсчитываемая по этой шкале, называется термодинамической; ноль этой шкалы называется нолем Кельвина.

 

Рис. 2. Изобары

Рис. 3. Изохоры

 

Вводя в формулы (2), (5) термодинамическую температуру, законам Гей-Люссака и Шарля можно придать более удобный вид:

(9)

(10).

Или для р = const, m = const, (11)

для V = const, m = const (12).

Практическая часть

Экспериментальная установка для исследования экспериментальных газовых законов приведена на рис. 4.

В стеклянном корпусе (1) находится шприц с подвижным поршнем (2). Под стеклянным корпусом, не касаясь его, расположена плитка (3). Датчик давления (4), подключают к входу S1 устройства Cobra (5). Короткая резиновая трубка-переходник (6) соединяет датчик давления со шприцом. Этот датчик позволяет автоматически производить измерение давления во внутренней камере шприца. Стеклянную емкость через отверстие (7) заполняют водой. В воду помещают магнитную мешалку. Можно перемешивать воду, обеспечивая равномерный прогрев воздуха во внутренней камере шприца, поднося магнит (9) к стеклянному корпусу (1). В отверстие (8), закрытое специальной пробкой с отверстием, помещают термодатчик (10), также подключив его к разъему S2 устройства Cobra (5).

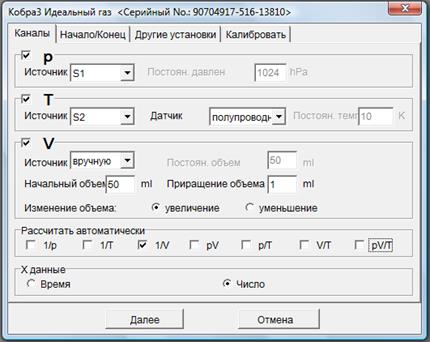
Рис. 4. Схема установки для исследования газовых законов.

1 – стеклянный корпус; 2 – подвижный поршень (шприц находится внутри стеклянного корпуса); 3 – плитка; 4 – датчик давления; 5 – устройство Cobra; 6 – резиновая трубка-переходник; 7, 8 – отверстия в стеклянном корпусе; 9 – магнит;10 – термодатчик.

Осуществить изотермический процесс можно при комнатной температуре, изменяя объем воздуха в шприце, перемещая поршень (2). Давление при этом будет меняться, что автоматически зафиксирует датчик давления (4). Температуру при этом будет фиксировать термодатчик (10).

Изобарический и изохорический процессы можно изучать одновременно. Температуру воздуха в шприце можно увеличить при нагревании воды, находящейся в стеклянном корпусе. Для этого используют плитку (3). Нагревание воздуха в шприце приведет к его расширению, поршень будет перемещаться таким образом, чтобы давление оставалось равным атмосферному (р = const). Фиксируя вручную изменение объема воздуха и соответствующую температуру по показаниям термодатчика (10), можно получить данные о зависимости V(T) для изобарического процесса.

В то же время, можно получить данные о зависимости р(Т) для изохорического процесса, возвращая поршень (2) в исходное положение (к начальному объему, то есть поддерживая V = const) после повышения температуры на определенную величину DТ (например, 5К). Давление автоматически будет фиксировать датчик давления (4).

Во всех случаях количество воздуха в шприце остается неизменным, то есть n = const.

Идея метода

Упражнение 1. Подготовка к работе.

1. Соберите установку в соответствии с рис. 4. Не подключайте пока трубку-переходник (6) к датчику давления (4).

2. Поместив стеклянную воронку в отверстие (7), заполните стеклянную емкость дистиллированной водой, поместите в воду магнитную мешалку, выньте воронку и закройте отверстие крышкой.

3. Резиновую трубку, закрепленную на «отростке» отверстия (7), опустите в стеклянный стакан для стекания жидкости при последующем нагревании.

4. Смажьте поршень шприца глицерином, чтобы предотвратить утечку воздуха. Поршень должен быть покрыт сплошной пленкой глицерина на протяжении всего эксперимента.

5. Перемещая поршень (2), установите начальный объем шприца V_o = 50 мл.

6. Подключите трубку (6) к датчику давления (4).

7. Подключите устройство Cobra к USB – порту компьютера.

Упражнение 2. Проверка закона Бойля – Мариотта.

1. Запустите программу для проведения измерений. Для этого на рабочем столе компьютера выберите ярлык программы Phywe Measure 4. В открывшемся окне в пункте меню Прибор > Кобра3 Идеальный газ. В появившемся диалоговом окне в закладке Каналы установите настройки измерений в соответствие с рис. 5.

Рис. 5. Окно настроек работы по изучению

изотермического процесса

 

2. В закладке Начало/Конец выберите «по нажатию клавиши».

Рис. 6а. Закладке Другие установки

Рис. 6б. Окно параметры дисплея

3. В закладке Другие установки поставьте флажки в поле Цифр. дисплей 1. В появившемся диалоговом окне в разделе Канал выберите Давление р в соответствии с рис. 6а, 6б. Поставьте флажок в поле Цифр. дисплей 2. В появившемся диалоговом окне в разделе Канал выберите Температура Т.

4. Поставьте флажок в поле Диаграмма 1, затем в появившемся диалоговом окне Параметры дисплея заполните поля в соответствии с рис. 7. В разделе Канал в поле давление р задается диапазон возможных значений давления. В разделе ось х в полях задается число возможных измерений. Рекомендуется в качестве максимального значения выбрать 20. В поле режим установите не автодиапазон.

Рис. 7. Окно Параметры дисплея

Рис. 8. Закладка Калибровать

5. Откалибруйте датчик. Для этого в закладке Калибровать введите в соответствующие поля значения комнатной температуры и давления, измеренные термометром и барометром соответственно.

6. Нажмите Далее взакладке Калибровать. На экране появится четыре окна: температура Т, давление р, Кобра3 - Измерение, окно для построения графика зависимости давления от числа измерений.

Рис. 9. Окно Измерение

7. Сохраните исходные данные измерения температуры Т_о, давления р_о, нажав на кнопку Сохранить значения в окне Измерение (рис. 9 ) илинажав Enter.

8. Рассчитайте число молей воздуха в шприце по (27) (V₁ – начальный объем воздуха, равный 50 мл)

9. Перемещая вращательным движением поршень (2) шприца вправо, увеличьте объем на 1 мл. Давление воздуха в шприце изменится. Сохраните результаты измерения давления и температуры, нажав кнопку Сохранить значения или Enter. Результаты измерений автоматически отображаются на графике зависимости р(V) на экране монитора.

10. Постепенно увеличивайте количество воздуха с шагом в 1 мл до объема 70 мл. Сохраняйте результаты измерения давления и температуры, нажимая кнопку Сохранить значения или Enter.

11. По окончании измерений нажмите кнопку Закрыть в окне Измерение (рис. 9). На экране появится окно с графиками зависимостей р, V, T, 1/V от числа измерений.

12. Для сохранения данных измерений в другой программе в пункте меню выберите Измерение > Экспорт данных и поставьте метки в полях Копировать в буфер и Экспортировать как число (рис. 10). Откройте программу, в которой вы будете обрабатывать данные и выберите Вставить.

 

Рис. 10. Окно Экспорт данных

Примечание: Для построения графиков можно воспользоваться возможностями программного обеспечения Phywe 4. Выберите пункт меню Измерение > Управление каналами. Например, для построения графика зависимости давления от объема, используя стрелки →, ←, →, ↓, заполните поля в окне Управление каналами в соответствии с рис.12. Нажмите Да, на экране появится график зависимости p(V)

 

Рис. 11. Окно Управление каналами

13. По экспериментальным данным на миллиметровой бумаге постройте график зависимости р(V).

14. Убедитесь, что график зависимости р(V) является гиперболой. Для этого линеаризируйте его, построив по экспериментальным данным график зависимости р(1/V) на миллиметровой бумаге.

15. Рассчитайте тангенс угла наклона g полученного графика методом парных точек или методом наименьших квадратов. Определите универсальную газовую постоянную по формуле (25), воспользовавшись результатами расчета числа молей воздуха, выполненными в п. 9.

16. Повторите измерения давления и объема 2-3 раза, используя указания пп. 1-15 (или пп. 1, 7-15, если настройки не нужно менять).

17. Проведите статистическую обработку результатов измерений R.

Приложение

Уравнение, которое связывает макроскопические параметры состояния для идеального газа, называют уравнением Менделеева – Клапейрона. Оно имеет вид

(1),

Сжимаемость идеального газа. Изотермический коэффициент сжимаемости. Свойство газа, как и всякого другого тела, изменять давление при изменении объема называется сжимаемостью. Если изменение объема происходит так, что температура газа при этом не меняется, то сжимаемость характеризуется изотермическим коэффициентом сжимаемости c, который определяется как относительноеизменение объема, вызывающее изменение давления на единицу. Очевидно, что

(2)

где dV – изменение объема газа, вызывающее изменение давления на величину dp; V– первоначальный объем (относительным изменением какой-либо величины и называется отношение изменения этой величины к ее первоначальному значению). Индекс Ту производной показывает, что она берется при Т = const.

Для идеального газа легко вычислить значение c. Продифференцировав уравнения состояния (1), и учтя, что , получаем:

(3)

Подставив (3) в (2), получим, что для идеального газа

(4).

Знак минус в выражении (4) указывает на то, что увеличение объема приводит к уменьшениюдавления. Изотермический коэффициент сжимаемости идеального газа равен, таким образом, обратной величине его давления и измеряется в системе СИ в единицах м²/Н. С ростом давления величина c уменьшается, так как чем больше давление, тем меньше у газа возможностей для того, чтобы еще больше сжиматься.

Список литературы

1. Матвеев А.Н. Молекулярная физика. – М. Высшая школа, 1981.

2. Кикоин А.К., Кикоин И.К. Молекулярная физика. – С.-Пб:Лань. 2008 – 484 с.

3. Иродов И.Е. Физика макросистем. – М.: Наука, 2004.

4. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Молекулярная физика. – М.: АСАDEMA, 2000.

5. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, т. 2, 3. 1981.

6. Трофимова Т. И. Курс физики. – М.: Высшая школа, 1998.

7. Шебалин О.Б. Молекулярная физика. – М.: Высшая школа, 1978.

8. Физический энциклопедический словарь. – М.: Советская энциклопедия, 1983.

Контрольные вопросы

1. Какой газ называется идеальным?

2. При каких условиях реальный газ можно считать идеальным?

3. Напишите уравнения состояния для идеального газа?

4. В чем заключается закон Бойля – Мариотта?

5. В чем заключается закон Гей-Люссака?

6. В чем заключается закон Шарля?

7. Каков физический смысл термического коэффициента давления?

8. Каков физический смысл термического коэффициента объемного расширения?

9. Выведите законы изопроцессов из уравнения состояния идеального газа.

10. Изобразите графики изопроцессов в координатах р(V), V(T), p(T).

11. Выведите формулы для расчета универсальной газовой постоянной, используемые в работе (25), (31), (35).

12. Выведите формулы (29), (33) для расчета термических коэффициентов, используемые в работе.

 

Лабораторная работа №46.

«Экспериментальные газовые законы»

Составитель: О. В. Сергеева, к.ф.-м.н., доцент

Рецензент: И. А. Малиненко, к.ф.-м.н., доцент

Цели работы:

1. Изучить понятие идеального газа.

2. Изучить экспериментальные газовые законы для идеального газа.

3. Изучить уравнение состояния идеального газа.

Задачи:

1. Проверить, является ли воздух, находящийся при атмосферном давлении и комнатной температуре идеальным газом.

2. Проверить выполнение экспериментальных газовых законов для воздуха.

3. Рассчитать универсальную газовую постоянную различными способами.

4. Рассчитать и сравнить между собой термические коэффициенты объемного расширения и давления для воздуха.

Приборы и принадлежности

1. Универсальная установка Кобра 3.

2. Источник питания на 12 В.

3. Датчик давления.

4. Программное обеспечение для изучения уравнения состояния газа.

5. Полупроводниковый датчик, -10..120 °C.

6. Стеклянный корпус.

7. Газовый шприц на 100 мл.

8. Нагреватель.

9. H-образная опора.

10. Магнит, магнитная мешалка.

11. Трубка-переходник для подключения датчика давления.

Идеальный газ

Системы, состоящие из большого числа молекул, называются макросистемами. К таким системам относятся, например, газ, жидкость, жидкие кристаллы, твердые тела, плазма.

Теоретическое изучение макросистем связано с большими трудностями, так как для этого требуется учесть все силы, которые действуют на каждую молекулу со стороны всех других. Если предположить, что движения молекул являются чисто механическими и подчиняются законам механики, то для полного описания всякой молекулярной системы нужно решить механическую задачу о движении всех молекул под действием заданных сил. Это значит, что должны быть написаны и решены уравнения движения, число которых равно числу молекул в данной системе (точнее говоря, число уравнений должно быть втрое больше, поскольку положение молекулы определяется тремя координатами, поскольку каждая молекула имеет три степени свободы). Если учесть, что, например, в 1 см³ газа при обычных условиях содержится 2,7 ^. 10¹⁹ молекул, то ясно, что не только решить, но даже написать такое число уравнений невозможно.

Но именно большое количество молекул делает ненужным рассмотрение движения каждой из них в отдельности. При таком большом числе частиц оказывается возможным ограничиться знанием лишь средних значений величин, характеризующих их движение: их средней скорости, средней энергии и т. д. Этим приемом и пользуются в молекулярно-кинетическом подходе при изучении молекулярных систем.

Из трех агрегатных состояний, в которых может находиться всякое вещество, наиболее простым является газообразное, так как в этом случае силы, действующие между молекулами, очень малы и ими при определенных условиях можно пренебречь. Будем считать, что межмолекулярные силы в них даже не малы, а полностью отсутствуют. Пренебрежем также размерами молекул, будем считать их материальными точками. При таких допущениях молекулы газа должны считаться совершенно свободными. Этозначит, что движутся они прямолинейно и равномерно, как всегда движутся тела, не подверженные действию каких-либо сил. Каждая молекула ведет себя, следовательно, так, как будто других молекул в сосуде нет. Газ, обладающий такими же свойствами, как и совокупность невзаимодействующих материальных точек, называется идеальным газом.

Таким образом, идеальный газ удовлетворяет следующим условиям:

1. Между молекулами газа отсутствуют силы взаимодействия на расстоянии;

2. Объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, т. е. молекулы газа можно считать материальными точками;

3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Идеальный газ – это модель, применяемая для описания реальных газов. Любой газ, находящийся в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах, близки по своим свойствам к идеальному.

Ученые используют модель идеального газа даже в сложных теоретических расчетах. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. Интересно, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. Дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия, то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов. Понятие «идеальный газ» используют также для описания свойств совокупности частиц различной природы: фотоны, электроны, фононы и т. д.

Экспериментальные газовые законы

Для изучения газовых систем достаточно знать только макроскопические параметры, характеризующие состояние всей системы. Такими параметрами для описания газовой системы, находящейся в тепловом равновесии, являются объем системы V, ее масса m, давление p и температура T. Равновесным состоянием системы называют такое состояние, при котором все ее макроскопические параметры сколь угодно долго остаются неизменными в отсутствии внешнего воздействия, при этом давление и температура имеют одинаковые значения во всех частях объема.

Исторически впервые установление связей между равновесными макроскопическими параметрами газовых систем произведено опытным путем. Экспериментальные газовые законы формулируются следующим образом:

1. Закон Бойля – Мариотта.

Для данной массы газа при постоянной температуре Т =const давление газа изменяется обратно пропорционально объему (закон Бойля – Мариотта):

рV = const (1)

Рис. 1. Изотермы идеального газа

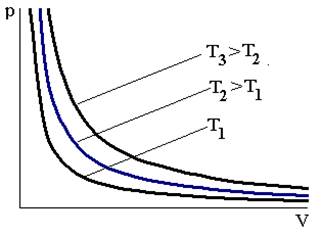
Формула (1), которую называют уравнением изотермы, и выражает закон Бойля – Мариотта. Закон был открыт Р. Бойлем в 1662 году, Э. Мариоттом в 1667 году. Закон Бойля – Мариотта показывает, как изменяется давление газа с изменением его объема при постоянной температуре и неизменной массе. Согласно этому закону при постоянной температуре для данной массы газа сжатие и расширение, т. е. изменение объема, сопровождается таким изменением давления, что произведение давления на объем остается величиной постоянной. Графически зависимость рот Vдля различных температур изображена на рис. 1. Из формулы (1) видно, что эти кривые, называемые изотермами, представляют собой гиперболы. Изотермы расположены на графике тем выше, чем выше температура, при которой происходит процесс.

Закон Гей-Люссака

Пусть теперь газ находится в условиях, когда постоянным сохраняется его давление р и масса,но изменяется температура. Такие условия можно осуществить, если поместить газ в цилиндр, закрытый легким подвижным поршнем. В таком цилиндре изменение температуры вызывает перемещение поршня и изменение объема, давление же остается постоянным. Для данной массы газа при постоянном давлении р = const объем газа изменяется линейно с температурой (закон Гей-Люссака):

(2),

где V_o – объем газа при 0^oС, V – объем газа при температуре t, a_p –термический коэффициент объемного расширения газа при постоянном давлении (или изобарический коэффициент объемного расширения газа, или изобарный коэффициент давления).

Уравнение (2), называемое уравнением изобары (процесс, происходящий при постоянном давлении, называется изобарическим), выражает закон Ж. Л. Гей-Люссака. Этот закон был открыт им в 1802 году.

Коэффициент объемного расширения a для любых вещество определяют как:

(3)

Индекс pу производной показывает, что она берется при p = const Для идеального газа в соответствии с выражением (2) он будет равен

(4)

Коэффициент объемного расширения представляет собой относительное изменение объема при изменении температуры на 1 К при изобарическом процессе. Относительное изменение объема определяется по отношению к объему, занимаемому газом при 0^оС.

Закон Шарля

Для данной массы газа при постоянном объеме V = const давление газа изменяется линейно с температурой (закон Шарля):

(5)

где р_о – давление газа при 0^оС, р – давление газа при температуре t, a_V – термический коэффициент давления газа для изохорического процесса (или изохорный коэффициент давления, или термический коэффициент давления).

Уравнение (5), называемое уравнением изохоры (процесс, происходящий при постоянном объеме, называется изохорическим), выражает закон Шарля. Этот закон был открыт им в 1787 году.

Термический коэффициент давления любого вещества для изохорического процесса определяют как

(6).

Индекс Vу производной показывает, что она берется при V = const. Для идеального газа в соответствии с выражением (5) этот коэффициент будет равен

(7)

Термический коэффициент объемного расширения представляет собой относительное изменение давления при изменении температуры на 1 К при изохорическом процессе. Относительное изменение давления определяется по отношению к давлению, соответствующему нормальным условиям, то есть при 0^оС.

Экспериментально установлено, что для идеального газа

(8).

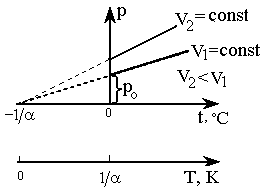
Согласно формулам (2) и (5), изобарический и изохорический процессы представляются на графиках прямыми линиями (изобарами и изохорами) (рис. 2, 3), проходящими наклонно к оси температур и пересекающими ее в точке , определяемой из условия 1 + at = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (рис. 2, 3), откуда Т = t + . Точка принята за начало отсчета новой шкалы температур, называемой термодинамической шкалой (шкалой Кельвина), или абсолютной шкалой. Температура, отсчитываемая по этой шкале, называется термодинамической; ноль этой шкалы называется нолем Кельвина.

 

Рис. 2. Изобары

Рис. 3. Изохоры

 

Вводя в формулы (2), (5) термодинамическую температуру, законам Гей-Люссака и Шарля можно придать более удобный вид:

(9)

(10).

Или для р = const, m = const, (11)

для V = const, m = const (12).