
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь с другими законами состояния идеального газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
А в форме пропорции С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году. В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений. С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки. С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение
Вопрос Газовой смесью понимается смесь отдельных газов, вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же оюъеме и при той же температуре, что и в смеси. Газовая смесь подчиняется закону Дальтона: ║Общее давление смеси газов равно сумме парциальных давлений ║отдельных газов, составляющих смесь.Р = Р1 + Р2 + Р3 +...Рn = ∑ Рi, (2.14)где Р1, Р2, Р3...Рn – парциальные давления. Состав смеси задается объемными, массовыми и мольными долями, которые определяются соответственно по следующим формулам:r1 = V1 / Vсм; r2 = V2 / Vсм; … rn = Vn / Vсм, (2.15) g1 = m1 / mсм; g2 = m2 / mсм; … gn = mn / mсм, (2.16) r1′ = ν1 / νсм; r2′ = ν2 / νсм; … rn′ = νn / νсм, (2.17)где V1; V2; … Vn; Vсм –объемы компонентов и смеси; m1; m2; … mn; mсм – массы компонентов и смеси; ν1; ν2; … νn; νсм – количество вещества (киломолей) компонентов и смеси. g1 + g2 + … + gn = 1. (2.20)Связь между объемными и массовыми долями следующее:g1 = r1∙μ1/μсм; g2 = r2∙μ2 /μсм ; … gn = rn∙μn /μсм, (2.21)где: μ1, μ2, … μn, μсм – молекулярные массы компонентов и смеси. Молекулярная масса смеси:μсм = μ1 r1 + r2 μ2+ … + rn μn. (2.22) Газовая постоянная смеси:Rсм = g1 R1 + g2 R2 + … + gn Rn = = Rμ (g1/μ1 + g2/μ2+ … + gn/μn ) = = 1 / (r1/R1 + r2/R2+ … + rn/Rn). (2.23) Удельные массовые теплоемкости смеси:ср см. = g1 ср 1 + g2 ср 2 + … + gnср n. (2.24) сv см. = g1ср 1 + g2сv 2 + … + gnсv n. (2.25) Удельные молярные (молекулярные) теплоемкости смеси: срμ см. = r1 срμ 1 + r2 срμ 2 + … + rnсрμ n. (2.26) сvμсм. = r1сvμ 1 + r2сvμ 2 + … + rnсvμ n. (2.27) Вопрос Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости
Вопрос При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
или в пределе при ΔVi → 0:
В изохорном процессе (V = const) газ работы не совершает, A = 0. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.Первый закон термодинамики для изотермического процесса выражается соотношением Q = A.Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.Работа газа в адиабатическом процессе выражается через температуры T1 и T2 начального и конечного состояний
Модель может быть использована в режиме ручного переключения кадров и в режиме автоматической демонстрации Вопрос Тема 2. ТЕПЛОЁМКОСТЬ ГАЗОВ 2.1.Массовая, объёмная и мольная удельные теплоёмкости Известно, что подвод теплоты к рабочему телу или отвод теплоты от него в каком-либо процессе приводит к изменению его температуры. Отношение количества теплоты, подведенной (или отведенной) в данном процессе, к изменению температуры называется теплоемкостью тела (системы тел):
где Теплоемкость численно равна количеству теплоты, которое необходимо подвести к системе, чтобы при заданных условиях повысить ее температуру на 1 градус. Так как единицей количества теплоты в СИ является джоуль, а температуры — градус К, то единицей теплоемкости будет Дж/К. В зависимости от внешних условий и характера термодинамического процесса теплота Поэтому обычно в выражении (2.1) при теплоёмкости
Индекс "x" означает, что процесс подвода (или отвода) теплоты идет при постоянном значении какого-либо из параметров, например, давления Ввиду того, что в термодинамике обычно рассматриваются квазистатические процессы теплообмена, теплоемкость
Опыты показывают, что количество теплоты, подведенное к рабочему телу системы или отведенное от него, всегда пропорционально количеству рабочего тела. Для возможности сравнения вводят, как известно, удельные величины теплоемкости, относя подведенную (или отведенную) теплоту количественно к единице рабочего тела. В зависимости от количественной единицы тела, к которому подводится теплота в термодинамике, различают массовую, объемную и мольную теплоемкости. Массовая теплоемкость — это теплоемкость, отнесенная к единице массы рабочего тела,
Единицей измерения массовой теплоемкости является Дж/(кг • К). Массовую теплоемкость называют также удельной теплоемкостью. Объемная теплоемкость — теплоемкость, отнесенная к единице объема рабочего тела,
где Объемная теплоемкость измеряется в Дж/(м3 • К). Мольная теплоемкость — теплоемкость, отнесенная к количеству рабочего тела (газа) в молях,
где Мольную теплоемкость измеряют в Дж/(моль • К). Массовая и мольная теплоемкости связаны следующим соотношением:
или
где Объемная теплоемкость газов выражается через мольную как
или
где
Вопрос Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.84.179 (0.009 с.) |

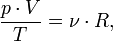

 — закон Бойля — Мариотта.
— закон Бойля — Мариотта. — Закон Гей-Люссака.
— Закон Гей-Люссака. — закон Шарля (второй закон Гей-Люссака, 1808 г.)
— закон Шарля (второй закон Гей-Люссака, 1808 г.) этот закон удобен для расчёта перевода газа из одного состояния в другое.
этот закон удобен для расчёта перевода газа из одного состояния в другое.


 — показатель адиабаты,
— показатель адиабаты,  — внутренняя энергия единицы массы вещества.
— внутренняя энергия единицы массы вещества. немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение
немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение 
 и средней кинетической энергией
и средней кинетической энергией 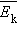 поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов
поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов

 ,
,
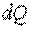 — элементарное количество теплоты;
— элементарное количество теплоты;  — элементарное изменение температуры.
— элементарное изменение температуры. может либо подводиться к рабочему телу, либо отводиться от него. Учитывая, что система участвует в бесчисленном множестве процессов, сопровождающихся теплообменом, величина
может либо подводиться к рабочему телу, либо отводиться от него. Учитывая, что система участвует в бесчисленном множестве процессов, сопровождающихся теплообменом, величина  для одного и того же тела может иметь различные значения. В общем случае значение теплоёмкости
для одного и того же тела может иметь различные значения. В общем случае значение теплоёмкости  .
.
 , объема
, объема  или других.
или других. .
. .
.
 ,
,
 — объем и плотность тела при нормальных физических условиях.
— объем и плотность тела при нормальных физических условиях.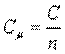 ,
,
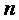 — количество газа в молях.
— количество газа в молях.
 ,
,
 - молекулярная масса.
- молекулярная масса.
 ,
,
 м3/моль — мольный объем газа при нормальных условиях.
м3/моль — мольный объем газа при нормальных условиях.



