
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гравитационный потенциал и уравнения движенияСодержание книги
Поиск на нашем сайте Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:
Подставляя выражение для лагранжиана L в уравнения Лагранжа:
Гравитационный потенциал и принцип эквивалентности Уравнения движения частицы в гравитационном поле в классической механике не содержат массы или другой величины, характеризующей частицу. Это является выражением основного свойства гравитационного поля — принципа эквивалентности. Гравитационный потенциал точечной частицы и произвольного тела Гравитационный потенциал точечной частицы равен: Для тела с произвольным распределением плотности массы Вопрос Первая К. с. υI на расстоянии r or центра Земли определяется по формуле Если в момент выхода на орбиту космический аппарат имеет скорость υ0 = υI, перпендикулярную направлению на центр Земли, то его орбита (при отсутствии возмущений) будет круговой. При υ0 < υI, орбита имеет форму эллипса, причём точка выхода на орбиту расположена в апогее. Если эта точка находится на высоте около 160 км, то сразу же после момента выхода на орбиту спутник попадает в лежащие ниже плотные слои атмосферы и сгорает. Т. о., для указанной высоты первая К. с. является минимальной для того, чтобы космический аппарат стал спутником Земли. На больших высотах космический аппарат может стать спутником и при υ0, несколько меньших υI, вычисленной для этой высоты. Так, на высоте 300 км космическому аппарату для этого достаточно иметь скорость на 45 м/сек меньшую, чем υI. Вторая К. с. υII на расстоянии r от центра Земли определяется по формуле Значения первой и второй К. с. для различных высот h, отсчитываемых от уровня моря на экваторе (h = r — 6378 км), приведены в табл. 1.
Первый закон Кеплера. Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |

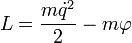 , где:
, где: 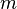 — масса частицы,
— масса частицы, 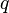 — координата частицы,
— координата частицы, 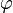 — потенциал гравитационного поля.
— потенциал гравитационного поля.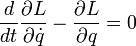 ,получаем уравнения движения
,получаем уравнения движения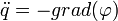 .
. , где
, где 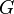 — гравитационная постоянная,
— гравитационная постоянная, 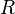 — расстояние от частицы. Эта же формула справедлива и для гравитационного потенциала любого тела со сферически-симметричным распределением плотности массы внутри него.
— расстояние от частицы. Эта же формула справедлива и для гравитационного потенциала любого тела со сферически-симметричным распределением плотности массы внутри него.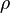 гравитационный потенциал удовлетворяет уравнению Пуассона:
гравитационный потенциал удовлетворяет уравнению Пуассона: 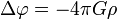 , где
, где  — оператор Лапласа,
— оператор Лапласа, 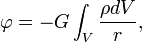 где r — расстояние от элемента объёма dV до рассматриваемой точки поля, а интегрирование производится по всему объёму тел, создающих поле. Гравитационный потенциал симметричного тела симметричен.
где r — расстояние от элемента объёма dV до рассматриваемой точки поля, а интегрирование производится по всему объёму тел, создающих поле. Гравитационный потенциал симметричного тела симметричен.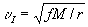 где f — постоянная тяготения, М — масса Земли. Принимается (см. Фундаментальные астрономические постоянные) fM = 398603 км3/сек2. В небесной механике эта скорость называется также круговой скоростью, т. к. в задаче двух тел движение по кругу радиуса r тела с массой m вокруг др. тела, обладающего несравнимо большей массой М (при М >> m), происходит именно с такой скоростью.
где f — постоянная тяготения, М — масса Земли. Принимается (см. Фундаментальные астрономические постоянные) fM = 398603 км3/сек2. В небесной механике эта скорость называется также круговой скоростью, т. к. в задаче двух тел движение по кругу радиуса r тела с массой m вокруг др. тела, обладающего несравнимо большей массой М (при М >> m), происходит именно с такой скоростью. υ0 = υII, тело с массой m в задаче двух тел будет двигаться относительно тела с массой М (при М >>m) по параболической орбите и удалится сколь угодно далеко, освобождаясь, в известном смысле, от гравитационного воздействиям. Скорости, меньшие параболической, называются эллиптическими, а большие — гиперболическими, т. к. при таких начальных скоростях движение в задаче двух тел с массами m и М (при М >> m) происходит по эллиптической или гиперболической орбитам соответственно.
υ0 = υII, тело с массой m в задаче двух тел будет двигаться относительно тела с массой М (при М >>m) по параболической орбите и удалится сколь угодно далеко, освобождаясь, в известном смысле, от гравитационного воздействиям. Скорости, меньшие параболической, называются эллиптическими, а большие — гиперболическими, т. к. при таких начальных скоростях движение в задаче двух тел с массами m и М (при М >> m) происходит по эллиптической или гиперболической орбитам соответственно.
 , где
, где  — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния),
— расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), 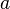 — большая полуось. Величина
— большая полуось. Величина  называется эксцентриситетом эллипса. При
называется эксцентриситетом эллипса. При 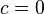 , и, следовательно,
, и, следовательно,  эллипс превращается в окружность.
эллипс превращается в окружность.


