
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй закон Кеплера (закон площадей)Содержание книги
Поиск на нашем сайте
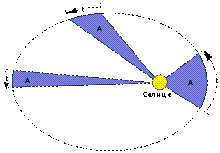
Второй закон Кеплера. Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Третий закон Кеплера (гармонический закон) Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.
Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды. 22 вопрос Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. ричина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо. Физический смысл Пусть тело движется со скоростью Тогда данное движение приведёт к изменению расстояния до центра вращения Как мы знаем, эта скорость движения равна Данное изменение будет равно:
Проведя дифференцирование по времени, получим С другой стороны, вектор
Общее ускорение будет Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется Тогда линейная скорость тела в неподвижной инерциальной системе координат равна:
где
Найдём значение каждого слагаемого в инерциальной системе координат:
где Таким образом, получаем:
Слагаемое Заметим, что если система S также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины Заметим также, что в частности, чтобы тело относительно неинерциальной системы отсчета двигалось прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к нему силу, которая будет противодействующей суммы Кориолисовой силы Вопрос Сила Кориолиса равна:
где Величина 24 вопрос По физической природе
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |


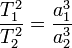 , где
, где  и
и 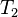 — периоды обращения двух планет вокруг Солнца, а
— периоды обращения двух планет вокруг Солнца, а 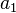 и
и 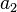 — длины больших полуосей их орбит.
— длины больших полуосей их орбит.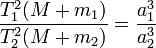 , где
, где  — масса Солнца, а
— масса Солнца, а 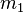 и
и 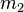 — массы планет.
— массы планет.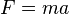 , где
, где 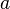 — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.
— кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.  Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности. вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).
вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).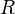 и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой — её переносной скорости.
и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой — её переносной скорости.
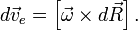
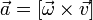 (направление данного ускорения перпендикулярно
(направление данного ускорения перпендикулярно 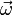 и
и 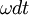 . Или приращение скорости будет
. Или приращение скорости будет при
при 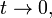 соответственно второе ускорение будет:
соответственно второе ускорение будет: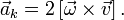 Как видно, система отсчёта не претерпела изменения угловой скорости
Как видно, система отсчёта не претерпела изменения угловой скорости  Линейная скорость относительно неё не меняется и остаётся
Линейная скорость относительно неё не меняется и остаётся 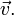 Тем не менее, ускорение не равно нулю.
Тем не менее, ускорение не равно нулю.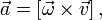 а также прибавляется ускорение в результате изменения центростремительного ускорения Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта S' со скоростью
а также прибавляется ускорение в результате изменения центростремительного ускорения Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта S' со скоростью  S' при этом сама движется поступательно с абсолютной линейной скоростью
S' при этом сама движется поступательно с абсолютной линейной скоростью  и одновременно вращается с угловой скоростью
и одновременно вращается с угловой скоростью 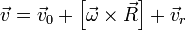 , причем
, причем 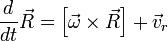
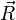 — радиус-вектор центра масс тела относительно неинерциальной системы отсчета S'. Продифференцируем данное уравнение:
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета S'. Продифференцируем данное уравнение: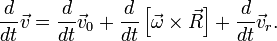
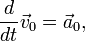
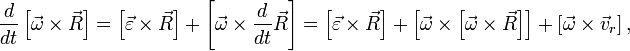
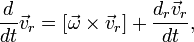
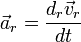 — линейное ускорение тела относительно системы S' в предположении её неподвижности,
— линейное ускорение тела относительно системы S' в предположении её неподвижности,  — угловое ускорение системы S'.
— угловое ускорение системы S'.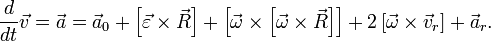
 и будет кориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений.
и будет кориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений. ,
,  для системы S' в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а
для системы S' в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а 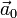 — абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.
— абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.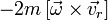 , переносной вращательной силы
, переносной вращательной силы  и переносной силы инерции поступательного движения системы отсчета
и переносной силы инерции поступательного движения системы отсчета 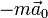 . Составляющая же ускорения
. Составляющая же ускорения  не отклонит тело от этой прямой так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение
не отклонит тело от этой прямой так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение 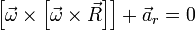 , которое если умножить векторно на
, которое если умножить векторно на 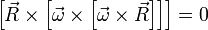 получим относительно
получим относительно  дифур
дифур  , имеющий при любых
, имеющий при любых  , которое и является уравнением такой прямой —
, которое и является уравнением такой прямой — 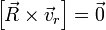 .
. ,
,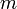 — точечная масса,
— точечная масса, 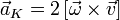 называется кориолисовым ускорением.
называется кориолисовым ускорением.


