Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второе начало термодинамики и «тепловая смерть Вселенной»Содержание книги
Поиск на нашем сайте Клаузиус, рассматривая второе начало термодинамики, пришёл к выводу, что энтропия Вселенной как замкнутой системы стремится к максимуму, и в конце концов во Вселенной закончатся все макроскопические процессы. Это состояние Вселенной получило название «тепловой смерти». С другой стороны, Больцман высказал мнение, что нынешнее состояние Вселенной — это гигантская флуктуация, из чего следует, что большую часть времени Вселенная все равно пребывает в состоянии термодинамического равновесия («тепловой смерти»)[3]. По мнению Ландау, ключ к разрешению этого противоречия лежит в области общей теории относительности: поскольку Вселенная является системой, находящейся в переменном гравитационном поле, закон возрастания энтропии к ней неприменим[4]. Поскольку второе начало термодинамики (в формулировке Клаузиуса) основано на предположении о том, что вселенная является замкнутой системой, возможны и другие виды критики этого закона. В соответствии с современными физическими представлениями мы можем говорить лишь о наблюдаемой части вселенной. На данном этапе человечество не имеет возможности доказать ни то, что вселенная есть замкнутая система, ни обратное. Вопрос Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:
где p — давление; V - объем T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная. Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка Для
где Таким образом, для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации:
Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации n. Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:
Окончательное уравнение:
Вопрос Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами.
На участке ВС не только давление, но и температура постоянны. Крайним точкам отрезка ВС соответствуют однофазные состояния вещества: точке С (объем Объем одного моля жидкой и газообразной фаз вещества соответственно равны:
Объем V содержит
После простых преобразований из выражения (5.1.2) находим искомое отношение
Умножая числитель и знаменатель левой части выражения (5.1.3) на молярную массу вещества, получим аналогичное отношение для масс жидкой и газообразной фаз:
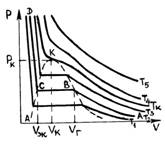
На рис. 1 представлены изотермы газа при различных температурах
Изотермы реального газа (схематично) Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния. Участок левее точки F — нормальная жидкость. Красная — критическая изотерма. Голубые — сверхкритические изотермы
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.008 с.) |

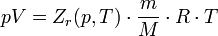
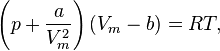
 — давление,
— давление,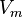 — молярный объём,
— молярный объём, — абсолютная температура,
— абсолютная температура,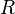 — универсальная газовая постоянная.
— универсальная газовая постоянная.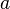 учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 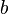 — объем молекул газа.
— объем молекул газа.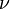 молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
молей газа Ван-дер-Ваальса уравнение состояния выглядит так: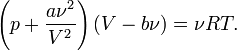
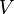 — объём,
— объём, 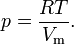
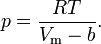
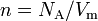
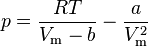
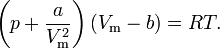
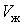 ) – жидкое, а точке В (объем
) – жидкое, а точке В (объем 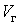 ) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей
) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей 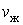 находится в жидком, а часть с количеством молей
находится в жидком, а часть с количеством молей 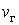 – в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме V.
– в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме V.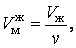
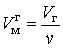
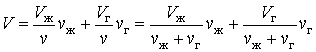
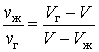
 Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре
Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре 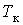 , называемой критической, стягивается в точку K. Изотерма, соответствующая температуре
, называемой критической, стягивается в точку K. Изотерма, соответствующая температуре