
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие колебания пружинного маятникаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Модель пружинного маятника. B — демпфер. F — внешняя сила (в примере не присутствует). Пусть имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение). Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления. Для упрощения вводятся следующие обозначения: Величину Тогда дифференциальное уравнение принимает вид
Сделав замену
Корни которого вычисляются по следующей формуле
Решения
Зависимость графиков колебаний от значения В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если
В этом случае колебания с самого начала экспоненциально затухают.
Если
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если
Тогда решением исходного дифференциального уравнения является
Где Константы ДЕКРЕМЕНТ ЗАТУХАНИЯ (от лат. decrementum - уменьшение, убыль) (логарифмический декремент затухания) - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону. T. к. в линейной системе колеблющаяся величина изменяется по закону Так, напр., для механич. колебат. системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф. упругости k и испытывающей трение силой FT, пропорциональной скорости v (F Т =- bv, где b - коэф. пропорциональности), Д. з.
При малом затухании
При малом затухании 29 вопрос Вынужденные колебания. Резонанс. Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или косинуса, то вынужденные колебания будут гармоническими и незатухающими. В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной. Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ0, происходит резкое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ0 внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний Ат от частоты вынуждающей силы υ представлен на рисунке, этот график называется резонансной кривой:
Явление резонанса играет большую роль в ряде природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. 30 вопрос СЛОЖЕНИЕ ОДИНАКОВО НАПРАВЛЕННЫХ КОЛЕБАНИИ. Рассмотрим сложение одинаково направленных колебаний одного периода, но отличающихся начальной фазой и амплитудой.Уравнения складываемых колебаний заданы:Х2 = А 2 • s in (сот -}- <рг), где х\, х2 — смещения; Ль А2 — амплитуды; фь фг — начальные фазы складываемых колебаний.2-4), на которой отложены векторы амплитуд AV и А2 складываемых колебаний под углами q>i и fj к оси ОХ иЕсли равномерно вращать систему векторов и проектировать векторы на ось OY, то их проекции будут совершать гармонические колебания в соответствии с заданными уравнениями.Отсюда следует вывод, что суммарное движение — гармоническое колебание, имеющее заданную циклическую частоту со.Найдем модуль амплитуды А результирующего колебания.Начальная фаза ср результирующего колебания определяется по тангенсу ее.10), видим, что при сложении одинаково направленных колебаний возможны следующие случаи.(можно считать, что q>i—ф2=0), то колебания однофазные и усиливают друг друга.результирующая суммарная амплитуда равна сумме амплитуд составляющих колебаний.2 = (2л + 1)«, колебания ослабляют друг друга и результирующая амплитуда равна разности амплитуд складываемых колебаний:колебания взаимно гасят друг друга.Если складываемые колебания имеют одинаковые амплитуды (А1=А2=А), но различные периоды, при этом периоды Т\ и Т2 отличаются незначительно друг от друга, т.разность периодов АТ = Т\—Т2 имеет небольшое значение, то при сложении таких колебаний наблюдаются биения.усиливают друг друга, и амплитуда суммарного колебания становится равной 2Л,-.При постепенном увеличении разности фаз в другие интервалы времени колебания становятся противофазными, и суммарная амплитуда обращается в нуль.Амплитуда сложного колебания при биениях изменяется со временем периодически.Число п биений в секунду (число повторений максимумов или минимумов в 1 сек) определяется разностью частот складываемых колебаний, т.Результирующая картина сложения колебаний при биенияхБиение можно наблюдать при звучании двух камертонов, если частоты их колебаний близки друг к другу.2-5 показана результирующая картина сложения колебаний при биениях.Таким образом, возвращающая сила пропорциональна смещению, и маятник при малых углах отклонения совершает гармонические колебания.Найдем выражение для периода колебаний математического маятника.Согласно этой формуле можно записать, что и тогда закон изменения периода колебаний запишется в виде r =: т.при постоянной длине маятника период его колебаний линейно зависит от расстояния до центра Земли. Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести.При небольших углах отклонения а физический маятник также совершает гармонические колебания.С учетом этого выражения формулу периода колебаний физического маятника можно записать в видеУ mgL — приведенная длина маятника, /— момент инерции относительно оси О колебаний, m — масса маятника, L — расстояние между центром тяжести С маятника и осью колебания О. 31 вопрос СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ. Остановимся на сложении колебаний материальной точки М, которая одновременно колеблется в двух взаимно перпендикулярных направлениях, например в направлении осей X и У (рис.Составляющие колебания имеют одинаковую частоту и фазу и различные амплитуды А\ и А2.Сложение взаимно перпендикулярных колебаний, имеющих одинаковые частоту и фазу = Al sin (от, = Л2 sin шт.Результирующее движение также является гармоническим колебанием, так как смещение, определяющее положение колеблющейся точки, согласно формулам (2.Фазы составляющих колебаний отличаются на я/2, а частоты равны.' Уравнения составляющих колебаний запишутся так:траекторией результирующего движения является эллипс с полуосями, равными амплитудам А\ и AZ 'Составляющих колебаний (рис.Сложение взаимно перпендикулярных колебаний, имеющих одинаковую частоту и разность фаз Л/2 a) S)В общих случаях сложения взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу (рис.Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.Для этого на горизонтальный вход осциллографа подают электрические колебания с частотой 50 гц, а на вертикальный вход — электрические колебания, частоту которых можно изменять.Изменяя эту частоту и тем самым соотношение частот составляющих колебаний, можно получить большой набор фигурПо-«этому можно сказать, что процесс распространения колебаний в данной среде есть волновойлфоцесс.Например, если закрепить один конец резинового жгута, а другой конец привести в колебание, то по длине жгута начнут распространяться колебания и возникнет волновое движение.Это графическое представление волнового процесса имеет совсем иной смысл, чем график смещения при гармоническом колебании, на котором изображалось смещение одной и той же точки в зависимости от времени (см.Точка / приводится в гармоническое колебание с периодом Т, направленное перпендикулярно линии /—5.Так как соседние точки связаны между собой упругими силами, они тоже приходят в колебание, но с некоторым запозданием.Колебание начали все точки, лежащие слева от точки 2.Прит=—Т точка / достигнет максимального отрицательносо смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4.Наконец, за время, равное периоду т=|Г, точка 1 вернется в положение равновесия, совершив полностью одно колебание.Колебания распространились до точки 5, все колеблющиеся точки образуют полную волну.При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5.Помимо поперечных волн, в среде могут возникнуть продольные волны, в которых колебания частиц среды происходят вдоль •направления распространения волнового процесса,.В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.В твердых телах, где наряду с упругими деформациями растяжения и сжатия есть упругая деформация сдвига, могут одновременно происходить и продольные, и поперечные колебания, т.Периодом волны Т называется время одного полного колебания ее точек. Волны со скоростью v распространяются от источника колебаний вдоль прямой.Уравнение колебаний точки В задано в таком виде х =Asin2itvT (242) где хв — смещение точки В, А — амплитуда ее колебаний, v — частота, т — время колебаний.Эти колебания дойдут до точки С через т', поэтому время колебаний точки С будет меньше t и составит (т —т').Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме х2 и х\:Каждая точка совершает гармоническое колебание с периодом Т.Физиологическое понятие — высота звука определяется частотой звуковых колебаний (физическая характеристика).С изменением частоты звуковых колебаний высота звука изменяется.В отличие от порога слышимости -порог болевого ощущения мало зависит от частоты колебаний.В том случае, когда имеется сложное 'периодическое движение, то его можно разложить на простые синусоидальные колебания.При этом частоты простых колебаний, например vb \z, vs и т., будут кратны частоте v основного колебания.Набор частот колебаний, присутствующих в данном звуке, называется его акустическим спектром.Процесс распространения звуковых волн в газах схематически можно представить следующим образом: источник механических колебаний передает эти колебания окружающим его газовым молекулам; в результате изменяется давление газа в данной микрообласти пространства.За время Т' приемник звука переместится на расстояние ±wT', а звук — на расстояние иТ', и тогда длина волны будет равна \ = иТ' ± wT' = (u ± о») Г', а частота звуковых колебаний, регистрируемых приемником, будет так какУльтразвуковые колебания могут быть получены с.Датчиком колебаний в акустических аппаратах обычно служит кварцевая пластина, заключенная между металлическими пластинами конденсатора, размеры которой определяют частоту ее собственных колебаний.При равенстве частоты электрических колебаний и одной из собственных частот колебаний пластины возникает резонанс, и кварцевая пластина становится источником сильных механических колебаний.Менее мощные ультразвуковые колебания с частотами порядка 700 тыс.В процессе колебаний атомов происходит переход потенциальной энергии в кинетическую и наоборот, т.Величина е = /zv называется к в а н т о м энергии при частоте колебаний v (h = = 6,62 • 10~34 дж • сек — постоянная Планка).Поэтому изменения энергии колебаний при невысоких температурах не наблюдаются.Возрастание температуры тела приводит к увеличению отклонений частиц при колебаниях от положений равновесия, что обусловливает тепловое расширение твердого тела.Внутренняя энергия твердого тела складывается из энергии колебаний его частиц.Колебания частиц для облегчения расчетов считаем гармоническими ') и независимыми друг от друга.Колебания атомов могут быть направлены по трем осям.Ч Силы, вызывающие колебания частиц в кристаллической решетке, не являются вазиупругими.В первом приближении можно считать, что они зависят от смещения х частиц по закону F = —kx+bx*, где член Ьх1 характеризует отклонение колебаний от гармонического характера.Под влиянием сил притяжения движение частиц превращается в тепловые колебания около узлов решетки.Пьезоэлектрические кристаллы широко применяются в качестве электромеханических преобразователей: стабилизаторов и фильтров радиотехнических частот, пьезоэлектрических манометров, излучателей и приемников ультразвуковых колебаний, пьезометров, звукоснимателей и т.Для работы в об- -ласти низких звуковых частот также применяются пластины, причем монтаж их ведется таким образом, чтобы они совершали колебания изгиба или кручения.Правило Матиссена утверждает, что зависимость удельногв электрического сопротивления от температуры р (Т) является ®* 259 сложной функцией, которая состоит из двух независимых слагаемых:, (8-38) где рост называется остаточным удельным сопротивлением, а рвд — идеальным удельным сопротивлением металла, которое соответствует сопротивлению абсолютно чистого металла и определяется лишь тепловыми колебаниями атомов.Если даже количество примесей и дефектов решетки свести к минимуму, то все-таки остается еще один фактор, влияющий на электрическое сопротивление металлов, — тепловое колебание атомов, которое, как утверждает квантовая механика, не прекращается и при тем'пературе(абсолютного нуля.В результате этих колебаний решетка перестает быть идеальной и в пространстве возникают переменные силы, действие которых приводит к рассеянию электронов, т.С точки зрения квантовой теории эти силь» появляются вследствие того, что электроны могут бмениваться фононами — квантами колебаний решетки.Электронные лампы используются в следующих целях: а) для преобразования переменного тока в постоянный (выпрямители); б) для усиления колебаний различных частот (усилители); в) для генерирования колебаний.Трехэлектродные лампы (триоды) широко применяются в радиоэлектронике и технике связи в качестве усилителей электрических сигналов и генераторов незатухающих колебаний.
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.68.121 (0.013 с.) |




 — сила сопротивления,
— сила сопротивления,  — сила упругости
— сила упругости ,
,  , то есть
, то есть


 называют собственной частотой системы,
называют собственной частотой системы,  — коэффициентом затухания.
— коэффициентом затухания.
 , получают характеристическое уравнение
, получают характеристическое уравнение


 , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид: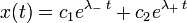
 , два действительных корня совпадают
, два действительных корня совпадают  , и решением уравнения является:
, и решением уравнения является:
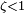 , то решением характеристического уравнения являются два комплексно сопряжённых корня
, то решением характеристического уравнения являются два комплексно сопряжённых корня

 — собственная частота затухающих колебаний.
— собственная частота затухающих колебаний. и
и  в каждом из случаев определяются из начальных условий:
в каждом из случаев определяются из начальных условий: 
 (где постоянная величина
(где постоянная величина  - коэф. затухания) и два последующих наиб. отклонения в одну сторону X1 и X2 (условно наз. "амплитудами" колебаний) разделены промежутком времени
- коэф. затухания) и два последующих наиб. отклонения в одну сторону X1 и X2 (условно наз. "амплитудами" колебаний) разделены промежутком времени  (условно наз. "периодом" колебаний), то
(условно наз. "периодом" колебаний), то  , а Д. з.
, а Д. з.  .
.
 . Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.
. Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з. .
. .
.
 вырождаются в отрезки прямых, а при разности фаз
вырождаются в отрезки прямых, а при разности фаз  и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.


