
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорения свободного падения маятником-стержнемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: построить график зависимости периода колебаний маятника-стержня от расстояния между верхним концом стержня и осью качания. Вычислить ускорение свободного падения. Оборудование: маятник-стержень, секундомер.
Описание установки и метода измерения
Большинство косвенных методов измерения ускорения свободного падения
В данной работе это достигается путем использования физического маятника в форме длинного стержня. Маятник представляет собой однородный стержень (рис. 1) с опорной призмой П, которую можно перемещать вдоль стержня и закреплять в любом его месте. Для определения положения призмы на стержне нанесена шкала с делениями через 1 см. Период колебаний маятника, который выражается формулой (1), можно записать в виде
где Момент инерции стержня относительно оси качания запишем по теореме Штейнера:
где J 0 момент инерции стержня относительно оси, проходящей через центр массы C (середину стержня) параллельно оси качания. Для стержня
Для любого тела момент инерции J 0 можно представить в виде
Величина a 0 называется радиусом инерции и имеет определенное значение для каждого тела. Для стержня
Используя формулы (3) и (4), получим выражение для приведенной длины
и периода колебаний
Таким образом, приведенная длина и, следовательно, период колебаний маятника являются функциями расстояния от центра массы до оси качания. Из этих формул видно, что L и T стремятся к бесконечности при двух значениях a: при a ® 0 и при a ® ¥. Для определения значений при которых период является экстремальным, найдем производную d L /d a и приравняем ее к нулю:
Из графика (риc. 2) видно, что при увеличении или уменьшении расстояния a по сравнению с a 0 период колебания увеличивается. Поэтому одно и то же значение периода, большее, чем T min, маятник может иметь при двух положениях опорной призмы: при
откуда
Приведенная длина (рис. 2) L = MN + MK. Очевидно, что другому периоду колебаний будет соответствовать другая приведенная длина. После подстановки (5) в (2) получим
откуда
Формула (6) является расчетной для вычисления ускорения свободного падения. Значения
Порядок выполнения работы
1. Опорную призму укрепить на конце стержня. Поместить маятник ребром опорной призмы на подставку и привести в колебательное движение так, чтобы амплитуда колебаний не превышала ~ 60. Это означает, что наибольшее отклонение нижнего конца стержня от положения равновесия не должно превышать 0,1 расстояния от конца до опорной призмы. 2. Определить секундомером время t десяти полных колебаний. Значения х и t записать в табл. 1. Таблица 1
3. Перемещать опорную призму к середине стержня через 0,01 м измеряя для каждого ее положения время 10 полных колебаний и занося результаты измерения в табл. 1. Измерения можно прекратить после того, как получится, что время 10 колебаний стало больше времени, полученного при самом первом измерении, когда опорная призма находилась на конце стержня. Перевертывать маятник и определять периоды для различных положений призмы на другом конце стержня нет необходимости.
5. Построить график T = f (x). Для этого по оси абсцисс откладывают расстояние х от конца стержня до опорной призмы, а по оси ординат – соответствующее значение периода. Масштаб по оси ординат следует выбрать по возможности больше, чтобы точнее определить по графику величины L и T. Для этого за начало отсчета по оси ординат нужно взять не нуль, а некоторое значение периода, меньшее Т min, но близкое к нему. Отметить на оси абсцисс середину стержня и провести через эту точку прямую, параллельную оси ординат. В итоге получится график, показанный на рис. 3. 6. По графику определить для 5 различных значения периода соответствующие им значений приведенной длины маятника L (см. формулу (5)). Для этого нужно провести 5 прямых, параллельных оси абсцисс так, чтобы каждая прямая пересекала построенную кривую в двух точках. Значения Т и L, определенные для каждой такой прямой, записать в табл. 2. Таблица 2
7. По формуле (6) вычислить
8. Вычислить относительную погрешность по формуле
Здесь
где 9. Вычислить абсолютную погрешность 10. Записать конечный результат в виде
Контрольные вопросы
1. Какие колебания называются гармоническими? Дать определение их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты). При каких условиях колебания физического маятника можно считать гармоническими? 2. Что называется физическим маятником? 3. Вывести формулу периода колебаний физического маятника. 4. Что называется приведенной длиной физического маятника? Вывести формулу (5). 5. Как определить точку подвеса, для которой период колебаний минимальный? Проверьте, соответствует ли расчетное значение экспериментальному? 6. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера. 7. Вывести расчетную формулу (6). 8. Почему для определения
Библиографический список.
1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 4.3, 27.1–27.2. 2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 16, 140–142. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 53–54. 4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл. 2 § 2.1–2.4. Гл.7 § 7.3, 7.4. 5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д.В.Сивухин. – М.: Физматлит МФТИ, 2005. – § 33, 42.
ЛАБОРАТОРНАЯ РАБОТА № 12 ПРУЖИННЫЙ МАЯТНИК
Цель работы: проверить закон Гука; определить жесткость пружины статическим и динамическим способами. Оборудование: пружина с линейкой, набор грузов, секундомер.
Краткая теория
Под влиянием внешних сил всякое твердое тело деформируется, т.е. изменяет свою форму и размеры. Упругой называется деформация, исчезающая с прекращением действия силы. Так, упруго растянутая пружина принимает свою прежнюю длину после прекращения действия растягивающей силы. С изменением знака силы меняется и знак упругой деформации. Например, если под влиянием растягивающей силы пружина удлиняется, то под влиянием сжимающей силы она укорачивается. По закону, установленному английским физиком Р. Гуком, величина деформации х пропорциональна действующей силе F: х ~ F. Под абсолютно твердым телом подразумевается такое тело, которое нисколько не деформируется под влиянием приложенных к нему сил. В природе нет неизменных, абсолютно твердых тел. Любое тело под действием сил испытывает большую или малую деформацию. Если при устранении внешних сил деформация исчезает, то тело называют упругим. Вообще под упругостью подразумевают присущее телам стремление восстанавливать измененную внешними силами форму. Одно и то же тело в зависимости от внешних условий (например, температуры или давления) может быть упругим или неупругим (пластичным). Так, с хорошей упругостью стальная пружина по мере повышения температуры становится всё более пластичной. Если на упругое тело действуют какие-либо внешние силы, то, согласно третьему закону Ньютона, и со стороны упругого тела на внешние тела действуют такие же, но противоположно направленные силы. Эти силы называют упругими силами. Поэтому закон Гука можно выразить и таким образом: при малых деформациях сила упругости пропорциональна деформации. Например, рассмотрим растянутую пружину. Если её длину из недеформированного состояния увеличили на х, то согласно закону Гука сила упругости пружины
где коэффициент k называется коэффициентом упругости или коэффициентом жесткости пружины. Положив в (1) х = 1, получим Это означает, что коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина увеличилась на единицу длины. Знак минус показывает, что сила упругости направлена в сторону, противоположную удлинению (смещению). Сила упругости пропорциональна смещению из положения равновесия и направлена к положению равновесия. Силы, не упругие по своей природе, но аналогичные им по виду зависимости от смещения, называются квазиупругими силами. К таким силам относятся, например, сила связи в атомах между ядром и так называемыми оптическими электронами. Груз на пружине, если отклонить его от положения равновесия и отпустить, будет совершать колебания около положения равновесия. Такая система носит название пружинного маятника. Колебания груза совершаются по закону синуса или косинуса и поэтому являются гармоническими. Уравнения колебаний, выражающие собой зависимость смещения груза от времени, имеют вид
В этих уравнениях А – амплитуда колебаний, т.е. величина наибольшего смещения груза от положения равновесия. Её значение зависит от величины первоначального отклонения или толчка, которым груз был выведен из положения равновесия. Постоянные величины
Для определения зависимости w от k запишем второй закон Ньютона для груза на пружине
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1000; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.01 с.) |

 основано на использовании формулы для периода гармонических колебаний физического маятника
основано на использовании формулы для периода гармонических колебаний физического маятника
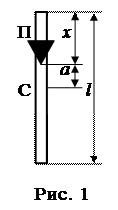 где J – момент инерции маятника относительно оси качания (точки подвеса), m – масса маятника, a – расстояние от центра массы до оси качания (см. рис. 1). Однако формула (1) непосредственно для вычисления
где J – момент инерции маятника относительно оси качания (точки подвеса), m – масса маятника, a – расстояние от центра массы до оси качания (см. рис. 1). Однако формула (1) непосредственно для вычисления  обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления
обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления 
 называется приведенной длиной физического маятника.
называется приведенной длиной физического маятника.
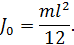

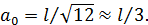
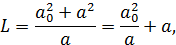


 откуда a = ± a 0.Значит, T = T min, если опорная призма закреплена на расстоянии a 0» l/3 от середины стержня. Второе расстояние a = a 0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы.
откуда a = ± a 0.Значит, T = T min, если опорная призма закреплена на расстоянии a 0» l/3 от середины стержня. Второе расстояние a = a 0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы. и
и  . Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (2):
. Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (2):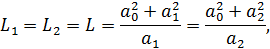
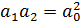 . Тогда
. Тогда
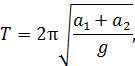

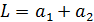 и T определяют по экспериментально построенному графику. Для этого опорную призму перемещают вдоль стержня и для каждого ее положения измеряют период колебаний. При проведении опыта и построении графика вместо расстояния a удобнее брать расстояние от конца стержня до призмы, которое на рис. 1 обозначено х.
и T определяют по экспериментально построенному графику. Для этого опорную призму перемещают вдоль стержня и для каждого ее положения измеряют период колебаний. При проведении опыта и построении графика вместо расстояния a удобнее брать расстояние от конца стержня до призмы, которое на рис. 1 обозначено х. 4. Вычислить периоды колебаний Т по формуле Т = t / n и занести в табл.
4. Вычислить периоды колебаний Т по формуле Т = t / n и занести в табл.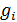 , м/с2
, м/с2
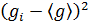


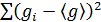
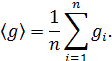

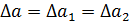 . Для нахождения
. Для нахождения  необходимо произвести измерения T пять раз для одного из значений x и вычислить абсолютную погрешность по формуле
необходимо произвести измерения T пять раз для одного из значений x и вычислить абсолютную погрешность по формуле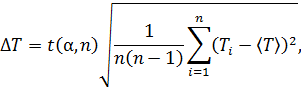
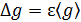 .
.
 .
.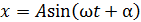 или
или 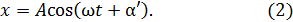
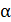 ,
,  представляют собой значения фазы в начальный момент времени t = 0 и называются начальной фазой колебания. Величина w есть круговая частота колебаний, она численно равна числу колебаний за 2π секунд. Продолжительность одного полного колебания называется периодом колебания Т. Период колебаний связан с круговой частотой соотношением
представляют собой значения фазы в начальный момент времени t = 0 и называются начальной фазой колебания. Величина w есть круговая частота колебаний, она численно равна числу колебаний за 2π секунд. Продолжительность одного полного колебания называется периодом колебания Т. Период колебаний связан с круговой частотой соотношением




