
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов прямых измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обычно в реальных измерениях присутствуют и случайные и систематические (аппаратурные) погрешности. Если вычисленная случайная погрешность прямых измерений равна нулю или меньше аппаратурной в два и большее число раз, то при вычислении погрешности косвенных измерений в расчет должна приниматься аппаратурная погрешность. Если эти погрешности отличаются меньше, чем в два раза, то абсолютная погрешность вычисляется по формуле
Случайная погрешность измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Поэтому задача элементарной обработки результатов измерений заключается в установлении интервала, внутри которого с заданной вероятностью находится истинное значение измеряемой физической величины. Пусть в результате прямых измерений физической величины получен ряд ее значений: Зная этот ряд чисел, нужно указать значение, наиболее близкое к истинному значению измеряемой величины, и найти величину случайной погрешности. Эту задачу решают на основе теории вероятностей, подробное изложение которой выходит за рамки нашего курса. Наиболее вероятным значением измеряемой физической величины (близким к истинному) считают среднее арифметическое
Здесь
где Вероятностью случайного события называется отношение числа случаев, благоприятных для данного события, к общему числу равновозможных случаев. Вероятность достоверного события равна 1, а невозможного – 0. Значение коэффициента Стьюдента, соответствующее заданной доверительной вероятности a и определенному числу измерений n, находят по табл. 1. Из таблицы видно, что величина коэффициента Стьюдента и случайная погрешность измерения тем меньше, чем больше n и меньше a. Практически выбирают a = 0,95. Однако простое увеличение числа измерений не может свести общую погрешность к нулю, так как любой измерительный прибор дает погрешность.
Таблица 1
Поясним смысл терминов абсолютная погрешность

Рис. 1
Если измерения той же величины повторить теми же приборами в тех же условиях, то истинное значение измеряемой величины Вычислив величину абсолютной погрешности Величина абсолютной погрешности
За меру точности измерения принимают величину 1/ε. Следовательно, чем меньше относительная погрешность ε, тем выше точность измерений. Таким образом, при обработке результатов прямых измерений необходимо проделать следующее: 1. Провести измерения n раз (обычно 5). 2. Вычислить среднее арифметическое значение 3. Задать доверительную вероятность a (обычно берут a = 0,95). 4. По табл. 1 найти коэффициент Стьюдента, соответствующий заданной доверительной вероятности a и числу измерений n. 5. Вычислить абсолютную погрешность по формуле (3) и сравнить ее с аппаратурной погрешностью. Для дальнейших вычислений взять ту из них, которая больше (см. пример на с. 8). 6. По формуле (4) вычислить относительную ошибку e. 7. Записать окончательный результат
с указанием относительной погрешности e и доверительной вероятности a. Обычно кроме прямых измерений в лабораторной работе присутствуют косвенные измерения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.185.28 (0.008 с.) |


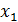 ,
,  , …,
, …, 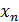 .
.
 – результат i -го измерения, n – число измерений. В случае малого n правильная оценка погрешности основана на использовании распределения Стьюдента (t – распределения). Случайная ошибка измерения может быть оценена величиной случайной абсолютной погрешности
– результат i -го измерения, n – число измерений. В случае малого n правильная оценка погрешности основана на использовании распределения Стьюдента (t – распределения). Случайная ошибка измерения может быть оценена величиной случайной абсолютной погрешности  , которую вычисляют по формуле
, которую вычисляют по формуле
 – коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности a. Значение доверительной вероятности a задает сам экспериментатор.
– коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности a. Значение доверительной вероятности a задает сам экспериментатор. и доверительная вероятность a, используя числовую ось. Пусть среднее значение измеряемой величины
и доверительная вероятность a, используя числовую ось. Пусть среднее значение измеряемой величины  (рис. 1), а вычисленная абсолютная погрешность
(рис. 1), а вычисленная абсолютная погрешность 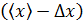 до
до  называется доверительным интервалом. Внутри этого доверительного интервала находится истинное значение измеряемой величины x.
называется доверительным интервалом. Внутри этого доверительного интервала находится истинное значение измеряемой величины x.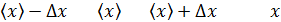
 попадет в этот же доверительный интервал, но попадание будет не достоверным, а с вероятностью a.
попадет в этот же доверительный интервал, но попадание будет не достоверным, а с вероятностью a. .
.



