
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение механических затухающих колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определить основные характеристики затухающих механических колебаний. Оборудование: специальная установка, снабженная секундомером, счетчиком числа колебаний и градусной шкалой-линейкой.
Общие сведения
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Наиболее простыми являются гармонические колебания, при которых какая-либо физическая величина, характеризующая колебание, изменяется со временем по закону синуса или косинуса. Примером может служить колебание маленького шарика, подвешенного на длинной нити. Если пренебречь силой трения, то величина смещения шарика из положения равновесия изменяется по закону
где A – амплитуда колебания; w0 – циклическая частота; a1, a2 – начальные фазы колебания. Колебательные процессы будут незатухающими, если они совершаются под действием только упругой или квазиупругой силы. В любой реальной колебательной системе всегда существует сила сопротивления, поэтому все реальные колебательные процессы затухающие. Отклоним шарик, подвешенный на нити, из положения равновесия (рис. 1). Применив к нему второй закон Ньютона, имеем
где m – масса шарика, a – ускорение, При малых колебаниях
Тогда уравнение (2) примет вид:
Уравнение (4) называется уравнением динамики затухающих гармонических колебаний, где b – коэффициент затухания. Если затухание невелико (b <w0), то решением уравнения (4) является выражение
Графически это решение представлено на рис. 2. Амплитуда затухающих колебаний изменяется по экспоненциальному закону. Следует отметить, что затухающие колебания не являются периодическими, т.к. через одинаковые промежутки времени состояние наблюдаемой системы в точности не повторяется. Однако эти колебания условно характеризуют частотой и периодом в том смысле, что колеблющаяся система проходит положение равновесия в одном и том же направлении через равные промежутки времени. Частоту затухающих колебаний определим по формуле
где Изучать затухающие колебания можно только при b < w0. При b > w0 колебания становятся апериодическими. Отметим, что в данной работе период затухающих колебаний незначительно отличается от периода свободных колебаний, т.е. b Для характеристики быстроты затухания колебаний вводят величину, называемую логарифмическим декрементом затухания d, который численно равен натуральному логарифму отношения двух амплитудных значений изменяющийся величины, отстоящих по времени одно от другого на период:
Выясним физический смысл этой характеристики. Пусть за t секунд амплитуда колебаний уменьшится в e раз. Тогда из (6), зная, что ln e = 1, имеем
Тогда из (6) с учетом (7) получим
где Из выражения (8) следует, что d есть величина, обратная числу колебаний Ne, совершенных системой за время, в течение которого амплитуда уменьшится в e раз. Время t называется временем релаксации. Скорость затухания колебаний характеризуется также физической величиной, называемой добротностью Q, которая может быть определена как отношение максимального значения квазиупругой силы к максимальной силе сопротивления:
Максимальное значение квазиупругой силы Максимальное значение силы сопротивления пропорционально максимальной скорости Тогда
Сделав замену ω0 = 2π/ T и учитывая (6), окончательно получим
Из выражения (9) следует, что добротность колебательной системы тем выше, чем большее число колебаний успевает совершиться, прежде чем амплитуда уменьшится в e раз. При слабом затухании добротность системы пропорциональна отношению энергии W, запасенной в системе, к убыли этой энергии
В этом заключается энергетический смысл добротности колебательной системы.
Описание установки
На передней панели прибора (рис. 3) имеются три клавиши: 1 (сеть) – выключатель сети; 2 (пуск) – запуск счетчика колебаний и секундомера; 3 (стоп) – остановка счетчика колебаний и секундомера. На стойке 4 подвешен металлический шарик 5. Амплитуду колебания шарика можно измерить по шкале 6. В работе определяются основные характеристики затухающих колебаний при различных силах сопротивления. Для изменения силы сопротивления плоскость колебания шарика ручкой 7 можно отклонить от вертикального положения на угол g, величину которого можно измерять по шкале 8. При этом шарик, совершающий колебания, начнет кататься по гладкой поверхности плоской панели. В этом случае сила сопротивления складывается из двух сил: силы вязкого трения шарика в воздухе, зависящей от скорости, и постоянной силы трения качения. При этом экспоненциальный закон затухания колебаний не нарушается.
Следует отметить, что при отклонении от вертикали плоскости колебаний на угол g изменяется период колебаний. Это обусловлено изменением квазиупругой силы F 1. В предельном случае, когда угол g = 90, 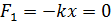 и колебания совершаться не будут. и колебания совершаться не будут.
Порядок выполнения работы
2. Задать начальную амплитуду A 0. По графику (рис. 4) определить амплитуду A τ последнего колебания, при котором начальная амплитуда уменьшится в e раз (A = A 0/ e). 3. Отклонить шарик из положения равновесия на A 0. Определить число колебаний Ne и время t, по истечению которого амплитуда примет значение A τ. 4. Опыты по пунктам 2 и 3 выполнить по 3 раза для 3-х значений угла наклона плоскости колебания шарика: 100, 200, 300. 5. Вычислить логарифмический декремент затухания и период колебаний
6. Вычислить коэффициент затухания и добротность колебательной системы
7. Вычислить коэффициент сопротивления
Результаты измерения занести в табл. 1. 8. Проанализировать изменение коэффициентов b и r, а также периода колебаний T в зависимости от угла наклона g плоскости колебаний. Таблица 1
Контрольные вопросы
1. Записать кинематическое уравнение гармонических колебаний и охарактеризовать все величины, входящие в него. 2. Записать дифференциальное уравнение затухающих колебаний и его решение. Изобразить это решение графически. 3. Что такое логарифмический декремент затухания? Объяснить силовой и энергетический смысл добротности колебательной системы. 4. Объяснить физический смысл коэффициента затухания и времени релаксации. Какова связь между этими величинами? 5. Каким образом изменяются коэффициенты r и b, а так же период колебаний системы T при увеличении угла наклона плоскости колебаний? 6. Каким образом на практике добиваются гашения колебаний?
Библиографический список
1.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 146. 2. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 49, 58. 3. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Ч.3. Гл. 2 § 2.1– 2.4. 4. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 3.5 § 3.8.
ЛАБОРАТОРНАЯ РАБОТА № 17
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 767; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.01 с.) |

 или
или 

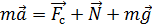 или
или 
 – квазиупругая сила,
– квазиупругая сила,  – сила сопротивления.
– сила сопротивления. , а
, а  , где x – смещение,
, где x – смещение,  – коэффициент сопротивления. Введем следующие обозначения:
– коэффициент сопротивления. Введем следующие обозначения:

 .
. 
 Здесь e – основание натурального логарифма.
Здесь e – основание натурального логарифма.
 – частота собственных колебаний системы при отсутствии силы сопротивления.
– частота собственных колебаний системы при отсутствии силы сопротивления. w0.
w0.


 – число колебаний, совершенных системой за время t.
– число колебаний, совершенных системой за время t.
 , где
, где  , (см. (3)).
, (см. (3)). , где
, где  (см. (3)).
(см. (3)).

 W за один период:
W за один период:

 1. Включить установку в сеть и проверить работу регистрирующих систем: электронного секундомера и счетчика числа колебаний.
1. Включить установку в сеть и проверить работу регистрирующих систем: электронного секундомера и счетчика числа колебаний.















