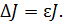Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение моментов инерции твердых тел методом крутильных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определить момент инерции тела, используя трифилярный подвес. Оборудование: трифилярный подвес, секундомер, штангенциркуль, образец для измерения.
Описание установки и метода измерений
Твердое тело, подвешенное на упругой нити, будет совершать крутильные колебания, если его повернуть на некоторый угол относительно вертикальной оси, совпадающей с нитью подвеса, и затем отпустить. Такие колебания происходят под действием упругих сил, возникающих при закручивании нити. Период гармонических крутильных колебаний зависит от упругости нити и момента инерции колеблющегося тела. В данной работе метод крутильных колебаний осуществляется путем применения трифилярного подвеса. Трифилярный подвес состоит из диска массой m, радиусом R (рис. 1), подвешенного на трех симметрично расположенных нитях длиной l. Наверху эти нити закреплены по краям диска меньшего радиуса r. При повороте диска на небольшой угол относительно вертикальной оси, проходящей через его центр, все три нити принимают наклонное положение, и диск начинает совершать крутильные колебания.
В процессе колебания диска его центр массы перемещается по оси вращения (рис. 1). Обозначим через h = h 1 – h 2 высоту, на которую поднимается центр массы диска при наибольшем отклонении его от положения равновесия. При этом потенциальная энергия диска
При возвращении диска к положению равновесия его потенциальная энергия переходит в кинетическую энергию вращательного движения
В момент прохождения положения равновесия кинетическая энергия принимает максимальное значение
где J – момент инерции диска, w0 – максимальная угловая скорость диска. Если пренебречь трением, то на основании закона сохранения энергии можно записать
При малых углах поворота диска (4º-6º) колебания можно считать гармоническими. Тогда угловое смещение диска от положения равновесия будет изменяться с течением времени по закону
где Мгновенная угловая скорость вращения определяется как первая производная углового смещения j по времени t
В момент прохождения диском положения равновесия угловая скорость диска максимальна и равна
Из формул (1) и (2) получим
Найдем величину h при повороте диска на угол
Из рисунка следует, что
Подставив
Вследствие малости угла
Подставив значение h в формулу (3),получим
Формула (5) является расчетной для вычисления момента инерции диска. Величину периода колебаний диска Т д измеряют в ходе опыта, а остальные величины указаны на установке. Если на диск положить тело произвольной формы так, чтобы центр массы его лежал на оси, вокруг которой совершаются колебания, то момент инерции всей системы J c определится по формуле
где m т – масса положенного на диск тела; T c – период колебаний системы. С другой стороны, момент инерции этой системы равен сумме моментов инерции диска и тела:
Таким образом, если из опыта по формулам (5) и (6) вычислить моменты инерции диска и системы, то момент инерции тела
Порядок выполнения работы.
1. Поворотом нижнего диска привести систему в колебательное движение. Следите за тем, чтобы центр масс диска не смещался в сторону, т.е. перемещался вертикально. Амплитуда колебаний не должна превышать 4º-6º. 2. Секундомером измерить время t д для 20 полных колебаний (n) и вычислить период колебаний T = t д/ n. Измерение повторить 5 раз. Результаты записать в табл. 1. Вычислить среднее значение периода Таблица 1
3. По формуле (5) определить момент инерции диска J д, подставляя среднее значение периода. Измерить (l, R, r). Значение m указано на установке. R и r равны радиусам дисков, если нить подвеса проходит через край диска. В противном случае за R и r надо брать расстояние от центров дисков до точки подвеса. 4. Сравнить момент инерции диска J д = mR 2/2, вычисленный по теоретической формуле, с экспериментальным результатом, полученным по формуле (5). 5. Поместить тело, момент инерции которого будем определять, на диск так, чтобы его центр массы находился на оси, вокруг которой совершаются крутильные колебания. 6. Провести измерения согласно п.п. 1-3 и вычислить J c по формуле (6). 7. Определить момент инерции тела по формуле (7). 8. Вычислить относительную погрешность измерения момента инерции диска
Подумайте, погрешностью каких величин можно пренебречь в приведенной формуле? 9. Найти абсолютную погрешность
Результат записать в виде J =... ±.... Контрольные вопросы 1. Что называется моментом инерции материальной точки относительно точки (полюса) и относительно оси вращения? От чего зависит момент инерции тела? Какую роль он играет во вращательном движении? 2. Вывести формулу момента инерции диска относительно оси перпендикулярной к диску и проходящей через центр инерции. 3. Что представляют собой крутильные колебания? 4. Какие колебания называют гармоническими? Что такое амплитуда, фаза, период, частота? Напишите кинематическое уравнение гармонических колебаний. 5. Что называется угловой скоростью? Как найти мгновенную угловую скорость при гармонических крутильных колебаниях? 6. Вывести формулу кинетической энергии вращающегося тела. 7. Вывести расчетную формулу (5).
Библиографический список 1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 4.3. 2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 16–17, 140–141. 3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 38, 39, 41, 53. 3. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл. 4 §4.4. Гл.7 § 7.1, 7.3, 7.4, 7.6. 4. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 33–36, 39,42. 5. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33. Гл. 3.2 § 3.3.
ЛАБОРАТОРНАЯ РАБОТА № 11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

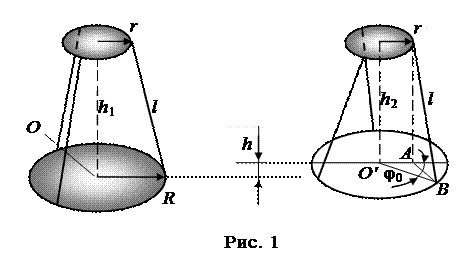
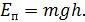




 – амплитуда углового смещения, T – период колебания диска.
– амплитуда углового смещения, T – период колебания диска.


 . Тогда (см. рис. 1)
. Тогда (см. рис. 1)


 и
и  в формулу (4),найдем
в формулу (4),найдем





 .
.
 , м/с2
, м/с2