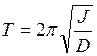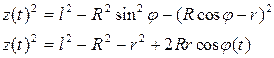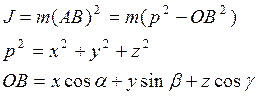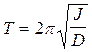Определение моментов инерции различных тел

Методом крутильных колебании

 

Цель работы: Определение моментов инерции различных тел с помощью крутильного маятника (трифилярного подвеса), проверка теоремы Штейнера-Гюйгенса.

Приборы и материалы: Трифилярный подвес, Установка ELWRO набор тел, весы, секундомер, штангенциркуль.

 

Период колебании крутильного маятника зависит от момента инерции и определяется формулой

где Т - период колебании маятника, D - коэффициент, зависящий от параметров установки, J - момент инерции тело относительно оси, проходящей через центр масс. В формулу входит неизвестная константа установки D которую необходимо исключить. Это делается различными способами:

1. На подвес маятника кладут тело с известным моментом инерции J ₀ и определяет период колебании полученного маятника T ₀. Затем это тело снимают и помещают тело с неизвестным моментом инерции J _x. Снова определяют период колебании Т _x. Неизвестный момент находится по формуле

2. Определяют период колебаний с телом с известным моментом инерции. Затем, не снимая с подвеса эталонного тела, кладут тело, момент которого надо измерить. Центры тяжести обоих тел при этом должны лежать на оси колебании маятника. Теперь период колебаний

Откуда

 

Упражнение 1

Определение момента инерции с помощью трифилярного подвеса

 

Состоящий из диска, массой m и радиуса R, подвешенного на трех симметричных нитях. Вторыми концами эти нити меньше радиуса r. При повороте одного из дисков на небольшой угол j₀ вокруг вертикальной оси все три нити принимают наклонное положение, а центр тяжести системы слегка поднимается вдоль оси вращения. Нижний диск начнет совершать крутильные колебания, период которых зависит от момента инерции и массы системы.

В любой момент времени координаты верхнего конца нити можно определить как r ₁ 0₁ 0

Координаты нижнего конца нити определяется как

 

Это дает

Координата z изменяется в пределах

Это дает изменение потенциальной энергии

и соответственно кинетической энергии колебаний

А полная энергия

Что дает

l – длина нити подвеса, равная расстоянию между дисками.

 

Измерения

 

1. Измерение момента инерции цилиндра

 

1. Осторожно повернуть нижний диск трифилярного подвеса, так чтобы не возникало поперечных колебаний, измерить период вращательных колебаний диска. Для этого, включив секундомер в момент прохождения одной из нитей подвеса мимо риски на стойке прибора, отсчитать 30 периодов колебаний и выключить секундомер. Повторить измерение 3 раза. Измерив r, R и l вычислить момент инерции ненагруженного диска. Масса диска 270 г.

Результаты свести в таблицу.

r

Dr

R

DR

l

Dl

T

DT

Jg

DJg

Jg+ц

Jц

D Jц

 

2. Положить на платформу трифилярного подвеса один из дисков. Повторитъ измерения п. 1и определить момент инерции диска.

3. Измерить момент инерции второго диска.

4. Измерить момент инерции двух дисков. Сравнить полученный результат с ожидаемой суммой моментов.

Все результаты занести в таблицу.

 

Проверка теоремы Штейнера

5. Положить на платформу оба диска так, чтобы они лежали на одном диаметре и на одинаковом расстоянии от центра платформы. Измерить расстояние центров масс дисков от центра платформы. При этом считать, что центр масс дисков находится на границе выреза в его закруглённой части. Повторить измерения п.I и определить суммарный момент инерции обоих дисков. Результаты свести в таблицу.

Сравнить полученные результаты с теоремой Штейнера.

 

Упражнение 2

Тензор инерции

Момент инерции при одной и той же массе оказывается различ­ным в зависимости от геометрии тела и положения оси вращения. Пусть ось вращения образует с осями координат углы a, b, g. Тогда момент инерции точки отно­сительно этой оси

 

Измерения.

Измерения проводятся на установке ELWRO с автоматическим счетом числа колебаний и времени.

1. Включить установку с сеть и прогреть ее в течении 5-10 минут. Нажать кнопку «пуск». После этого установка готова к работе. Определить момент инерции рамки. Для этого отклонить рамку на небольшой угол, отпустить и нажать кнопку «сброс». Отсчет числа колебаний начинается автоматически. При появлении в окне счета колебаний числа 19 нажать кнопку «стоп». Отсчет времени и числа колебаний автоматически останавливается после отсчета времени и числа колебаний. Определить период колебаний рамки Т₀. Повторить измерения 5 раз и найти среднее значение Т₀.

Для определения момента инерции необходимо знать коэффициент упругости проволоки. Его, однако можно исключать, используя тело с легко вычисляемым моментом инерции, например, цилиндр или диск. Период колебаний

Тогда для рамки без дополнительного тела

а для рамки с цилиндром или параллелепипедом

откуда

 

Установить в рамку цилиндр. Для этого, вставив цилиндр в рамку осторожно двумя пальцами сжать рамку так, чтобы кулачки рамки вошли в отверстие на поверхности цилиндра, после чего затянуть стопорные винты на рамке и зажать верхний кулачок.

Установить цилиндр в рамку вертикально и измерить период колебаний. Повторить измерения 5 раз и найти среднее значение.

Установить цилиндр в рамке горизонтально и снова определить период колебаний. Повторить измерения 5 раз и найти среднее значение.

Установить в рамке диск и измерить период колебаний с диском. Повторить измерения 5 раз и найти среднее значение.

Измерить размеры цилиндра и диска и вычислив моменты инерции определить момент инерции рамки. Результаты свести в таблицу.

Цил. верт.	Цил. гор.	Диск	JB	JГ	JД	J0	ТВ	ТГ	ТД

 

2. Установить в рамке один из параллелепипедов. Измерить период колебаний рамки с параллелепипедом и определить момент инерции параллелепипеда. Измерения повторить для следующих положений параллелепипеда:

1. Закрепить параллелепипед в отверстиях, находящихся в центре малых граней параллелепипеда (относительно оси z).

2. Закрепив параллелепипед в отверстиях в центре больших граней моменты (относительно осей х и у).

3. Закрепив параллелепипед в отверстиях, проходящих через середину большого ребра (момент инерции J_ху).

4. Закрепив параллелепипед в отверстиях, проходящих через противоположные углы параллелепипеда (большая диагональ).

5. Закрепив параллелепипед в отверстиях, проходящих через середины противоположных коротких ребер (малая диагональ).

Все измерения повторить 5 раз. Определить среднее значение периодов колебаний и моменты инерции для каждого положения.

 

Результаты свести в таблицу.

Jz	Jх	Jу	Jхyz	Jхy	Jzx

 

3. Измерить длину ребер параллелепипеда. Рассчитать направляющие косинусы диагоналей. Построить тензор инерции и сравнить полученные значения моментов инерции с измеренными.

 

Контрольные вопросы

1. Что называется моментом инерции? Какую роль он играет в описании движения тел?

2. В чем отличие крутильных колебаний от колебаний физического маятника?

3. Что такое тензор? Как рассчитать момент инерции тела относительно произвольной оси, проходящей через центр масс?

4. Сформулировать теорему Штейнера. Как определяется момент инерции тела относительно оси?

5. Что такое момент силы?

6. Написать основные формулы вращательного движения.

7. Почему натяжение нитей трифилярного подвеса должно быть одинаковым?

8. Под действием какой силы трифилярный подвес совершает крутильные колебания?

9. Как выражается модуль кручения проволоки круглого сечения через размеры проволоки и модуль сдвига материала, из которого сделана проволока?

10. Можно ли определить момент инерции тела неправильной формы и как это можно сделать?

11. Сформулируйте основной закон динамики вращательного движения твердого тела.

 

Лабораторная работа № 13