
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислить доверительный интервал измерения модуля ЮнгаСодержание книги
Поиск на нашем сайте
DЕ=d × Е. Записать окончательный результат в виде Е = < Е > ±Dе,Р = 0,67. 2. Определение модуля упругости методом изгиба
Рассмотрим изгиб однородного бруска (балки) произвольного поперечного сечения, которое должно оставаться одинаковым на протяжении всей длины бруска. Пусть до деформации брус имел прямолинейную форму. Проводя сечение АВ и А' и B' нормальные к оси бруска, мысленно вырежем из него бесконечно малый элемент AA' и ВВ' длина которого l0 (рис. 5).
Рис. 5
Ввиду бесконечной малости выделенного элемента можно считать, что в результате изгиба прямые АА', NN', ВВ' и все прямые, параллельные им, перейдут в окружности с центрами на оси 0, перпендикулярной к плоскости рисунка (рис.6). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линий NN при изгибе удлиняются, волокна лежащие ниже линии NN'—укорачиваются. Длина линии NN' остаётся неизменной. Эта линия называется нейтральной линией.
Рис. 6
Проходящее через неё сечение (не деформированного) бруса плоскостью, перпендикулярной к плоскости рис.6, называется нейтральным сечением. Таким образом, все наружные волокна будут растянуты, все внутренние – сжаты. Пусть R - радиус кривизны нейтральной линии NN¢. Тогда l 0= R *a, где a - центральный угол, опирающийся на дугу NN¢. Рассмотрим волокно бруса, находящееся на расстоянии x, от нейтрального сечения. Величина x положительна, если волокно находится выше нейтрального сечения (рис.6) и отрицательно, если оно находится ниже. Если брус не слишком толст, так что /x/<<R то длина рассматриваемого волокна будет l =(R +x)*a, а удлинение:
D l = l - l 0=x*a
Следовательно, напряжение, действующее вдоль рассматриваемого волокна
Напряжение, таким образом, меняется линейно с расстоянием x. Ниже нейтрального сечения оно отрицательно, то есть является давлением. Сумма сил напряжения или сжатия одинаковая для всех волокон. Она может быть учтена особо и исключена из рассмотрения, когда речь идет об изгибе в чистом виде. Поэтому мы будем считать, что сумма всех сил натяжения, действующих в каждом нормальном сечении бруса, равна нулю, то есть или ò s × dS = 0или òx × dS = 0, где dS – элемент площади рассматриваемого поперечного сечения. Интегрирование ведется по всему поперечному сечению бруса. Очевидно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса. Из соотношения òs dS = 0 следует, что момент сил напряжения Мs,действующих на сечение В, не зависит от того, относительно какой оси он берется. Для вычисления М проще всего взять ось, перпендикулярную к плоскости рисунка и проходящую через точку N. Очевидно,
где I = òx2 × dS
Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако, в отличие от последней, I есть чисто геометрическая величина с размерностью четвертой степени длины. Если поперечное сечение бруса имеет форму прямоугольника с шириной а и высотой, b, то
Действительно, dS = а × dx (рис. 6). Значит
Направим ось Х вдоль нейтральной линии недеформированного бруса. Ось Y направим к ней перпендикулярно и расположим в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y = y(x). По известной формуле
если изгиб мал (Y ¢<<1) то квадратом первой производной можно пренебречь. В этом приближении
Определим теперь стрелу прогиба балки, жесткозакрепленной в стенеодним из своих концов (рис. 7).
Рис. 7
На другой конец балки действует сосредоточенная сила F. Весом самой балки будем пренебрегать. Стрелой прогиба мы называем смещение свободного конца балки под действием приложенной силы F. Поместим начало координат в точке О, в которой нейтральная, линия балки пересекается с плоскостью стены. Через произвольную точку В (х) (с координатой х =(В) проведем нормальное сечение. Для равновесия необходимо, чтобы сила F действующая на часть ВА со стороны части OВ, была направлена вверх и равнялась F. Вместе с О она образует пару сил с моментом М == F(l – х), где l - длина балки. Момент силы напряжения возьмём в приближённом виде, считая, что прогиб мал. Это приводит к уравнению
E × I × Y"=F (l-x) Ось Y направлена в сторону вогнутости, то есть вниз. При таком условии вторая производная Y" положительна, и обе части последнего соотношения имеют одинаковые знаки. Интегрируя это уравнение один раз, получим
Постоянная интегрирования С равна нулю, так как при х = 0, то есть в точке О, касательная к нейтральной линии горизонтальна. Интегрируя вторично и учитывая, что в точке О (то есть при х = 0) у =0, найдём
Полагая здесь x = l находим стрелу прогиба (у =l)
l = F×l 3 / 3 EI
Учитывая что
По стреле прогиба l при данной сосредоточенной нагрузке F и зная размеры бруса, можно определить модуль Юнга материала бруса:
Е =4 F × l 3 / аlb 3
Рис.8 Прибор рис.8 представляет собой раму, установленную на опорах. На раме установлен индикатор, который может перемещаться вдоль рамы и служит для измерения величины прогиба бруса. Брус закреплён с одной стороны неподвижно. На незакреплённой стороне бруса имеется опорная призма с подвеской для гирь. Она также может перемещаться вдоль бруса. 1. Установите опорную призму в месте, где кончается сужение бруса (сдвинуть призму вдоль стержня влево до упора). 2. Измерьте микрометром высоту бруса в нескольких местах и найдите его среднее значение. 3. Измерьте длину стержня (расстояние от места закрепления до опорной призмы). 4. Измерьте штангенциркулем ширину бруса в месте его закрепления и в месте подвеса грузов и найдите среднее значение по формуле:
5. Установите стрелку индикатора на нуль и постепенно нагружайте стержень дополнительным и грузами (1 кг, 2 кг, З кг и т.д.) делая каждый раз отсчет по индикатору. 6. Снимая дополнительные грузы в обратном порядке, снова зафиксируйте показания индикатора. 7. Проделайте изложенное в пунктах (5) и (6) по 3 раза. 8. Данные измерений занесите в таблицу
9. По данным измерений постройте график зависимости lср — f (F) проверьте, выполняется ли закон Гука. 10. Вычислите модуль Юнга стали для нагрузки F =5кГ и сравните полученный результат с табличным значением. 11. Вычислите абсолютную и относительную погрешности измерения. Контрольные вопросы
1. Почему в данной работе, наблюдая деформацию изгиба, можно определить модуль Юнга, характеризующий деформацию одностороннего растяжения (сжатия). 2. Какая деформация называется упругой, какая - пластической? 3. Перечислите основные виды деформации? 4. Запишите выражение для плотности энергии упругой деформации для случая деформации одностороннего растяжения и для случая деформации сдвига. 5. В чём заключается явление упругого гистерезиса? Какую роль играет площадь петли гистерезиса? - 6. Запишите закон Гука для основных видов деформации. Что такое модуль упругости? Приведите его название и обозначение для различных видов деформации. 7. Что характеризует коэффициент Пуассона? 8. В чём заключается явление упругого последействия?
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |



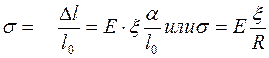




 Мs =Е × I × Y ¢¢
Мs =Е × I × Y ¢¢
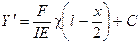

 , получим l= F ×l 34 / аb 3Е
, получим l= F ×l 34 / аb 3Е




