
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращательное движение твёрдого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вращательное движение твёрдого тела характеризуется двумя особенностями: 1. Всe точки тела движутся по замкнутым круговым траекториям. 2. Скорости различных точек тела при этом оказывается различными, поэтому обычные методы описания, используемые при описании прямолинейного (поступательного) движения оказываются непригодными для описания вращательного движения. Можно, однако, описывать вращательное движение формулами, аналогичными формулам для поступательного движения, введя новые физические величины, аналогичные массе, скорости, силе и т.д., используемые при описании прямолинейного движения. При вращении вокруг некоторой оси изменение положения тела можно характеризовать углом поворота вокруг этой оси, который будет одинаковым для всех точек тела, подобно пути при поступательном движении. Тогда соответственно первая и вторая производные от угла поворота по времени также будут одинаковыми для всех точек тела и их следует называть соответственно угловой скоростью и угловым ускорением. Скорость точки и линейное ускорение могут быть получены как векторное произведение радиус-вектора точки относительно оси вращения на угловые скорость или ускорение.
Угол поворота при этом считается вектором, а его направление определяется по обычному правилу определения направления аксиальных векторов - вектор угла, угловой скорости, или ускорения, соответственно вектор перемещения, линейной скорости и линейного ускорения и радиус-вектор точки должны образовывать правую тройку векторов. Теперь если для каждой точки можно использовать произведение углового ускорения на радиус-вектор, то второй закон Ньютона приобретает вид удобно представить его в виде
Тогда уравнение движения можно свести к виду аналогичному уравнениям для прямолинейного движения.
где J - момент инерции точки, В случае твердого тела, когда на тело, а не на отдельные точки его действует сила, уравнение приобретает вид
Соответственно импульс заменяетсямоментом импульса
а кинетическая энергия приобретает вид
где Отличие описания вращательного движения от прямолинейного заключается в определении момента инерции, который зависит от формы тела. Вращательное движение обладает рядом особенностей. 1. Пpи вращательном движении скорость точки постоянно изменяется по направлению. Поэтому даже при постоянной угловой скорости всегда имеется центростремительное ускорение
не изменяющее величины линейной скорости. 2. Если при равномерном вращении тело движется вдоль радиуса, то очевидно линейная скорость тела изменяется
Это приводит к появлению ещё одного ускорения - ускорения Кориолиса определяемого как
4. Если на ось вращения действует сила, стремящаяся повернуть ось вращения, то возникает движение в направлении перпендикулярном как оси вращения, так и моменту пары сил - прецессия, скорость которой
Лабораторная работа № 7 Проверка основного закона динамики вращательного движения твёрдого тела с помощью маятника Обербека Цель работы: экспериментальное изучение законов динамики вращательного движения с помощью маятника Обербека. Приборы и принадлежности: прибор Обербека, штангенциркуль, миллиметровая линейка, электрический секундомер, набор грузов. Установка Elwro.
Маятник Обербека представляет крестовину, укрепленную на двойном шкиве. Ось вращения крестовины устанавливается горизонтально и закреплена в подшипниках (рис. 15). Вращение прибора осуществляется с помощью нити, намотанной на шкив. Изменение силы натяжения производится с помощью грузов различной массы, прикрепленных к свободному концу нити. Изменение момента инерции прибора достигается передвижением четырех грузов одинаковой массы и формы по направляющим крестовины. Уравнение вращательного движения прибора (при пренебрежении силами трения) связывает три величины: момент силы натяжения нити, угловое ускорение и момент инерции прибора Момент силы натяжения нити и угловое ускорение можно вычислить, зная ускорение а поступательного движения подвешенного груза.
Рис. 15
Ускорение определяется по значениям расстояния, пройденного грузом и соответствующего промежутка времени. Таким образом, можно рассчитать момент инерции прибора с помощью величин, измеренных в эксперименте. Для падающего груза
Основное уравнение динамики вращательного движения для вращающейся части маятника.
Второй закон Ньютона для поступательно движущегося груза массой М в проекции на направление движения. М × а = М × g - T Отсюда
а для момента инерции J z получается следующее выражение:
где М - масса груза, подвешенного к нити; r — радиус шкива; h — расстояние, пройденное грузом; t — время, за которое груз прошел расстояние h; g — ускорение свободного падения.
Упражнение 1
Определение момента инерции и момента силы трения в маятнике Обербека, проверка соотношения Mz=Jze. 1. Укрепить грузы на крестовине маятника. Сбалансировать маятник. Для этого сначала закрепить 2 диаметрально противоположных груза и слегка толкнуть маятник. Проследить за тем, как он будет вращаться и останавливаться. При правильной балансировке замедление вращения должно быть равномерным, а окончательное положение маятника безразличным. После этого закрепить оставшиеся два груза и снова проверить балансировку. При необходимости сместить грузы. 2. Изменяя величину груза на нити, измерить 7-8 раз угловое ускорение при фиксированном положении грузов на крестовине. Построить график зависимости e от М×r. Определить из него момент инерции и момент силы трения. Момент инерции равен Ctg угла наклона графика. Момент силы трения – точка пересечения графика с осью M r. Снять грузы с крестовины и определить таким же образом момент инерции крестовины без груза J0 Сравнить полученный результат с формулой J = J o+ 4 mR 2 + 4 ml 2 + где R - расстояние от центра масс грузов на крестовине до оси вращения, l - высота груза на крестовине, p - его радиус. Результаты занести в таблицу.
Таблица
Упражнение 2 Проверить правильность соотношения 3. При постоянной массе груза, подвешенного на нити измерить угловое ускорение и момент инерции для двух различных положений грузов на крестовине. Проверить выполнение соотношения Результаты занести в таблицу. Экспериментальную проверку уравнения движения можно осуществить двумя способами: 1. При неизменном моменте инерции прибора должно сохраняться соотношение. J = 2. При постоянной массе груза, подвешенного к нити (при постоянном моменте силы) должно выполняться соотношение J11 – J12 = 4 m (R 12 – Rl22) где m – масса грузов крестовины, R 1 и R 2 – расстояние от оси вращения до центра тяжести грузов крестовины.
Контрольные вопросы: 1. Что называется моментом силы относительно точки и относительно неподвижной оси? 2. От чего зависит момент инерции тела, какую роль он играет во вращательном движении? 3. Как в данной работе определяется ускорение поступательного движения грузов, подвешенных к нити прибора; получите выражение для расчёта - этого ускорения. 4. Чем обусловлена разница в экспериментальном и теоретически полученных значениях момента инерции? 5. На каком законе основана данная работ? Сформулируйте этот закон. 6. Какая связь существует между линейным и угловым ускорениями? При каком условии она существует? 7. Момент какой силы приводит маятник Обербека во вращательное движение? Как можно изменить момент силы в данной работе? 9. Какая теорема используется для вычисления момента инерции цилиндров? Как влияет на момент инерции цилиндров расстояние, на котором они расположены на стержнях? 10. Как влияет на угловое ускорение увеличение момента силы при неизменном моменте инерции? Как влияет на угловое ускорение увеличение момента инерции при неизменном моменте силы? Лабораторная работа № 8
Маховое колесо
Цель работы: определить момент инерции махового колеса и момент сил трения. Приборы и принадлежности: маховое колесо, секундомер, штангенциркуль, линейка, угольник.
Маховое колесо представляет собой массивное тело, вращающееся на подшипниках вокруг горизонтальной оси. На вал колеса радиуса r наматывается нить с подвешенным грузом массы m (рис. 16). Опускаясь с некоторой высоты h1, груз раскручивает колесо и, достигнув нижней точки, начинает подниматься вверх за счет запасенной кинетической энергии колеса. При отсутствии сил сопротивления высота подъема груза h 2 была бы равна h 1 в соответствии с законом сохранения механической энергии. В действительности же, ввиду действия сил трения в подшипниках, сопротивления воздуха, а также выделения тепла в нити, груз поднимается на несколько меньшую высоту. В рассматриваемом случае главной причиной потерь энергии является действие сил трения. Известно, что если в замкнутой системе действуют неконсервативные силы (например, силы трения), то работа этих сил равна изменению полной механической энергии системы: D E = E 2 - E 1 = A тр.
Рассмотрим систему колесо-груз в крайних положениях h 1 и h 2, когда кинетическая энергия равна нулю, т.е. механическая энергия системы равна потенциальной энергии груза. Тогда D E = E 2 - E 1 = mgh 2 - mgh 1 = A тр = -
где М тр- модуль момента сил трения. Знак «минус» в правой части указывает на то, что работа сил трения отрицательна. Интеграл берется в пределах полного угла поворота колеса при опускании и подъеме груза. Момент сил трения можно считать практически не зависящим от скорости вращения, т.е. постоянной величиной. Следовательно. А т р= - М тр Dj. Пусть h 1 и h 2 отсчитываются от нижнего положения груза. Груз при движении проходит расстояние h 1+ h 2, а колесо поворачивается на угол
В результате
Рис. 16 На колесо действуют только две силы с отличными от нуля моментами – сила натяжениянити Т и сила трения (рис.16). Поэтому закон движения S МI = Je, запишется в виде: T×r - M тр = Je, где e - угловое ускорение колеса. Второй закон Ньютона для груза: mg – T = ma, где а – ускорение груза. Учитывая, что тангенциальное ускорение точек обода вала равно ускорению груза (нить нерастяжима) а = а t, а = er. Так как сила трения постоянна, то ускорение постоянно, т.е. применимо уравнение равноускоренного движения
где t 1 – время опускания груза. Окончательно
где d = 2 r – диаметр вала.
Измерения
1. Измерить диаметр вала колеса и диаметр нити. Найдите их сумму d. 2. Поднимая груз на одинаковую высоту h 1, несколько раз измерить время опускания груза t 1 и высоту подъема h 2. Результаты измерений занести в таблицу. Таблица
Оценить ошибки прямых измерений. Записать окончательные результаты в виде
J=<J> + SI, Mтр=<Мтр > + SM.
Контрольные вопросы
1. Проанализировать полученные результаты. 2. Что называется моментом силы, моментом инерции и угловым ускорением? 3. Основной закон динамики вращательного движения. 4. Вывести расчетные формулы. Какие упрощающие предположения сделаны при их выводе? 5. Оценить потери энергии в нити и сравнить с потерями в подшипниках. 6. Найти основные источники погрешностей. Предложить методы их уменьшения. Лабораторная работа № 9 Прецессия гироскопа
Цель работы: изучение особенностей движение гироскопа под действием внешних сил. Приборы и материалы: Установка ELWRO
Гироскопом называется твердое тело, вращающееся с большой угловой скоростью вокруг оси симметрии. В этом случае можно считать что направление векторов момента количества движения и мгновенной угловой скорости совпадают с направлением оси симметрии, поэтому о движении вектора момента количества движения можно судить по движению оси симметрии гироскопа. Гироскоп закрепляется таким образом, чтобы он мог свободно вращаться вокруг трех взаимно перпендикулярных осей. Центр тяжести гироскопа находится в точке пересечения осей и при любом повороте гироскопа остается на месте. Таким образом, центр тяжести гироскопа оказывается закрепленным, а все движения сводятся к вращению относительно центра тяжести. Движения гироскопа под действием внешних сил описывается уравнением моментов.
где
Скорость прецессии связывает угловую скорость вращения гироскопа, его момент инерции и момент внешних сил. Поэтому измеряя две из них можно найти третью. Например, момент внешних сил
а момент инерции
Установка ELWRO (рис. 17) представляет собой гироскоп в виде ротора асинхронного двигателя. Для увеличения момента инерции на вал ротора насажен массивный стальной диск. Скорость вращения гироскопа может достигать 12 000 оборотов в минуту. Электродвигатель закреплен в вертикальной вилке в которой он может в небольших пределах поворачиваться вокруг горизонтальной оси, перпендикулярной оси ротора. В свою очередь вилка может вращаться вокруг вертикальной оси.
Рис. 17
Таким образом, возможно вращение ротора вокруг любой из трех осей или вокруг любого направления в пространстве. Электронная схема установки включает в себя систему регулировки и измерения скорости вращения ротора. На роторе укреплен диск с отверстиями через каждые 5о, освещаемые лампой измерителя скорости вращения. Через отверстия диска освещается фотодиод датчика, который вырабатывает импульсы тока, считаемые счетным устройством. Скорость вращения диска измеряется как скорость счета этих импульсов и выводится на стрелочный индикатор. С вертикальной осью также связан такой же диск для измерения угла поворота вертикальной оси. Величина угла поворота выводится на цифровой индикатор. В схему входит также измеритель времени с точностью до 10-3с. Схемы отсчета углов и времени включаются и выключается автоматически. При нажатии кнопки «сброс», устанавливаются нулевые показания счетчиков оборотов и времени и дается разрешительный импульс на включение схемы. Включение осуществляется импульсом от счетчика оборотов. Таким образом осуществляется точная привязка начала счета времени к шкале угла поворота вертикальной оси. При нажатии кнопки «стоп» выдается импульс, разрешающий выключение счетчика времени. Само выключение осуществляется импульсом счетчика оборотов. Измерения
1. Включить прибор в сеть и прогреть в течение 10-15 минут. 2. Убедиться, что гироскоп может вращаться вокруг горизонтальной и вертикальной осей, гироскоп должен вращаться легко, без заметного сопротивления. 3. Уравновесить гироскоп. Для этого, перемещая противовес на рычаге гироскопа, добиться, чтобы при небольших вертикальных отклонениях, гироскоп возвращался к горизонтальному положению, заметить положение противовеса на рычаге, так как в дальнейшем отсчет плеча вращающего момента будет отсчитываться от этого положения (около 3 см деления). 4. Включать двигатель и дождаться установления постоянной скорости вращения. Сместить противовес на 0,5 – 1см от положения равновесия и нажать кнопку «сброс». В результате прецессии гироскопа включается счетчик времени и счетчик угла поворота. После поворота на угол 300 нажать кнопку «стоп». Счетчики автоматически выключатся при повороте на угол 400. Измерить скорость прецессии. Изменяя скорость от 1000 до 6000 оборотов в минуту проследить за изменением скорости прецессии.
Результаты свести в таблицу.
Построить график зависимости скорости прецессии от угловой скорости вращения гироскопа. 5. При фиксированной скорости вращения гироскопа 3000 – 4000 оборотов в минуту измерить зависимость скорости прецессии от плеча груза, смещая его каждый раз на 5 мм от положения равновесия до конца шкалы в обе стороны. Свести данные в таблицу и построить график зависимости скорости прецессии от вращающего момента.
6. Из построенных графиков определить момент инерции гироскопа. Примечание. Гироскоп может быть сбалансирован недостаточно точно – центр тяжести не совпадает с точкой пересечения осей вращения. Это приведет к заклиниванию вертикальной оси при некоторых углах поворота при вращающемся роторе. Поэтому при работе необходимо выбирать такие углы поворота, при которых заклинивание не происходит.
Контрольные вопросы
1. Что называется гироскопом? 2. Что называется моментом инерции? Что называется моментом импульса? Что называется моментом силы? 3. Как рассчитываются моменты инерции, импульса и силы? 4. Что такое прецессия гироскопа?
4. Колебательное движение
При колебательном движении тело периодически проходит через одну и ту же точку (состояние) двигаясь в противоположных направлениях. В простейшем случае такое движение возникает, если сила направлена против скорости и пропорциональна смещению
Движение, при котором смещение изменяется по синусоидальному закону, получило название гармонических колебаний. В общем случае колебательное движение может происходить по сложному закону. Однако, любую периодическую функцию можно представить в виде ряда Фурье, состоящего из гармоник – синусов или косинусов. Поэтому любое сложное периодическое движение может быть представлено как сумма гармонических. Период колебаний равен
Кинетическая и потенциальная энергия соответственно равны
Нетрудно видеть, что кинетическая и потенциальная энергия переходят друг в друга, а максимальное их значение равно полной энергии
Уравнение, включающее силы трения решается относительно просто только в случае силы трения, пропорциональной скорости. В этом случае уравнение приобретает вид
а его решение
Величина
Лабораторная работа №10 Колебания маятников
Цель работы: изучить колебания математического и физического маятника. Определить ускорение свободного падения из периода колебаний математического, физического и оборотного маятников. Приборы и материалы: Оборотный маятник, секундомер, линейка, установка ELWRO.
Упражнение 1. Математический маятник. В физике маятником называют твердое тело, которое может совершать под действием силы тяжести колебания относительно неподвижной горизонтальной оси. Простейшим маятником является математический – массивное тело исчезающих малых размеров, подвешенное на тонкой нерастяжимой нити. Движение мятника можно охарактеризовать углом отклонения от вертикали. Тогда как и в случае вращательного движения
где J – момент инерции, М – вращающий момент – момент силы тяжести. Момент инерции шарика, подвешенного на нити относительно точки название 0 при условии пренебрежения массой нити. J = Если радиус r мал, по сравнению с длиной нити a, тогда можно считать, что: J = ma
M= mg a sin
Это дает уравнение колебаний маятника:
и период колебаний маятника T = 2 a – угол отклонения маятника. 1. Включить установку и прогреть ее в течение 5-10 минут. Прежде чем выполнять работу необходимо определить диапазон, изохронности колебаний. Отклонив мятник на расстояние 3 см от положения равновесия (при длине мятника 50 см) нажать кнопку «пуск» и отпустить маятник. Прибор автоматически начинает отсчет числа колебаний и времени при прохождении шариком положения равновесия. При появлении отсчета числа колебании 29 нажать кнопку «стоп». Отсчет прекратится при 30 колебаниях. Повторить измерения для 5,7,10,15 см. Построить график зависимости периода колебаний от начальной амплитуды. 2. Изменяя длину маятника каждый раз на 5см, измерить период колебаний в зависимости от длины. Построить график зависимости Т от 3. Определить ускорение свободного падения.
Упражнение 2. Физический маятник В математическом маятнике предполагается, что точечная масса, образующая маятник, совершает только поступательное движение. Это предположение удобно тем, что позволяет перенести полученное решение на поступательное движение, например, колебания груза на пружине. На практике, однако, маятник всегда совершает кроме колебаний, поворот вокруг оси колебаний, который необходимо учитывать путем введения момента инерции и записи уравнений колебаний относительно угла поворота маятника. Тело произвольной формы и произвольного распределения масс, совершающее колебания вокруг горизонтальной оси под действием силы тяжести принято называть физическим маятником. В простейшем случае физический маятник представляет собой стержень, для которого момент инерции относительно точки подвеса
где m - масса стержня, l – его длина; a – расстояние центра масс до точки подвеса. Период колебаний в этом случае
для малых колебаний, позволяющих не учитывать Измерения проводятся со стальным стержнем l =552,2 мм снабженным опорной призмой высотой 18,1 мм. При перемещении призмы по длине стержня центр масс может смещаться в пределах 4 см поэтому маятник снабжен второй призмой – противовесом, который следует устанавливать симметрично первой относительно середины стержня. Смещая положение призм каждый раз на 2,5 см измерить зависимость периода колебаний маятника от а. Для этого слегка отклонив маятник, нажать на кнопку «сброс» и при появлении в окошке счетчика числа колебаний числа 29 нажать кнопку «стоп», счетчик времени покажет время 30 периодов колебаний. Построить график зависимости периода колебаний от а. Особенностью графика является то, что при некоторой геометрии период колебаний маятника оказывается наименьшим и почти не зависит от а. Это дает возможность довольно точно определить ускорение свободного падения. Для полученного минимального значения Т установить соответствующие значения а и измерить период колебаний по 100 колебаниям. Провести измерение периода колебаний 3 раза и вычислить
Упражнение 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.014 с.) |




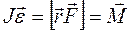

 - момент силы,
- момент силы, 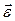 -угловое ускорение.
-угловое ускорение.


 момент инерции тела.
момент инерции тела.











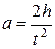 .
.








 - момент внешних сил относительно точки пересечения осей,
- момент внешних сил относительно точки пересечения осей, 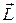 - момент количества движения гироскопа J -момент инерции гироскопа. Отсюда следует что ось вращения гироскопа под действием внешних сил поворачивается в направлении действия момента внешних сил, т.е. прецессирует. Скорость прецессии
- момент количества движения гироскопа J -момент инерции гироскопа. Отсюда следует что ось вращения гироскопа под действием внешних сил поворачивается в направлении действия момента внешних сил, т.е. прецессирует. Скорость прецессии





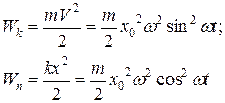



 , соответствующая уменьшению амплитуды за период получила название логарифмического декремента затухания колебаний.
, соответствующая уменьшению амплитуды за период получила название логарифмического декремента затухания колебаний.


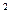
 = mg a
= mg a 


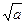 . При измерениях амплитуды выбирать в соответствии с первым пунктом работы, так чтобы отклонение периода колебаний от среднего не превышало 0,5%.
. При измерениях амплитуды выбирать в соответствии с первым пунктом работы, так чтобы отклонение периода колебаний от среднего не превышало 0,5%.






