
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематические уравнения движенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Система отсчета. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой. Поскольку движение тел совершается с течением времени, то для его описания необходимо выбрать начало отсчета времени и масштаб времени. Итак, элементами системы отсчета, необходимыми для описания движений, являются: начало отсчета, масштабы отсчета расстояний, три направления отсчета положения тел, начало отсчета времени, масштаб времени. Кинематические уравнения движения
Рис. 1.1 Если с выбранными телами отсчета мы связали какую-либо систему координат, то движение тела можно изучать относительно этой системы координат. Для определения положения тела в пространстве обычно пользуются декартовой системой координат x,y,z (рис. 1.1). Положение точки M относительно системы отсчета можно задать с помощью трех ее декартовых координат x,y,z представляющими собой расстояния от этой точки до координатных плоскостей yz, zx, xy соответственно. Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчета времени. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение. Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением Поступательное и вращательное движения — самые простые примеры механического, движения тел. Пример: При движении автомобиля по дороге его кузов движется поступательно, а колеса совершают вращательное движение относительно осей.
Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, перемещается параллельно сама себе.(кабина лифта). При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела), так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и параллельны между собой, также равны и параллельны между собой ускорения всех точек.
3.Динамика материальной точки. 1 закон Ньютона. Интегральные системы отсчета. Предметом динамики является изучение движения материальных тел под действием сил. Понятие о силе было введено в статике. Силы в статике мы считали постоянными. В динамике наряду с постоянными силами рассматриваются силы, изменяющиеся по модулю и направлению. В динамике при изучении движения принимают во внимание инертность тел. Инертность проявляется в том, что тело сохраняет движение в отсутствие действующих на него сил, а когда силы начинают действовать, то скорости точек тела меняются не мгновенно, а постепенно и тем медленнее, чем больше инертность тела. Количественной мерой инертности является масса тела. В общем случае движение тела зависит еще и от распределения масс в теле. В качестве материальных объектов в механике рассматриваются материальная точка, абсолютно твердое тело и система материальных точек или тел. Материальной точкой называется точка, обладающая массой. Абсолютно твердое тело – это материальное тело, в котором расстояния между двумя любыми точками остаются неизменными. Механической системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех остальных. Материальная точка - это модель материального тела любой формы, размерами которого в конкретной задаче можно пренебречь. Первый закон динамики (закон инерции): материальная точка при отсутствии внешних воздействий сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к ней силы не изменят этого состояния. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции. Свойство тел сохранять свою скорость неизменной называется свойством инертности. Количественной мерой инертности материальной точки является ее масса. Инерциальной называется система отсчета, в которой справедлив закон инерции. Реально система отсчета будет считаться инерциальной в результате опытной проверки выполнения в ней закона инерции. При решении большинства технических задач за инерциальную можно принять систему отсчета, связанную с Землей. Теорема Гюйгенса — Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где m — полная масса тела. Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Для вывода этого закона рассмотрим простейший случай вращательного движения материальной точки. Разложим силу Касательная сила вызовет появление касательного ускорения. В соответствии со вторым законом Ньютона Ft=mat или F cos a=mat. Выразим касательное ускорение через угловое: at=re. Тогда F cos a=mre. Умножим это выражение на радиус r: Fr cos a=mr2e. Введём обозначение r cos a = l, гдеl — плечо силы, т.е. длина перпендикуляра, опущенного из оси вращения на линию действия силы. Посколькуmr2 =I — момент инерции материальной точки, а произведение Получили основной закон динамики вращательного движения: момент силы равен произведению момента инерции на угловое ускорение. Этот закон аналогичен второму закону Ньютона Замечая, что e=dw/dt, из (4.4) получаем:
Произведение момента силы М на время её действия dt называется импульсом момента силы. Произведение момента инерции I на угловую скоростьw называется моментом импульса тела: L=Iw. Тогда основной закон динамики вращательного движения в форме можно сформулировать следующим образом: импульс момента силы равен изменению момента импульса тела. В такой формулировке этот закон аналогичен второму закону Ньютона. 7.Механическая работа. Кинетическая и потенциальная энергия. Мощность. Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения
В СИ единицей работы является джоуль (Дж). Кинетическая энергия Когда сила, приложенная к телу, больше силы сопротивления, то результирующая сила приводит тело в движение. Движущееся тело обладает кинетической энергией. Работа по ускорению тела тратится на увеличение его скорости, т.е. увеличение кинетической энергии: K = 1/2(mV2) Мощность Мощность - это скорость выполнения работы за единицу времени P = W/t (Дж/с) или (Вт)
Мощность является скалярной величиной!
Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника меняет свое положение координата его центра масс, при переменном токе меняют свои характеристики с определенной повторяемостью напряжение и ток в цепи. Колебательный процесс может имет различную физическую природу, поэтому различают колебания механические, электромагнитные и др. Но различные колебательные процессы характеризуются одинаковыми физическими параметрами и одинаковыми уравнениями. Отсюда вытекает целесообразность единого подхода к исследованию колебаний различной физической природы. Например, единый подход к исследованию механических и электромагнитных колебаний использовался английским физиком Д.У.Рэлеем (1842—1919), русским инженером-экспериментатором П. Н. Лебедевым (1866—1912), А.Г.Столетовым. Большой вклад в развитие теории колебаний сделали Л. И. Мандельштам (1879—1944) и его ученики.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.
Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
откуда
Величина, обратная периоду колебаний,
т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний
(где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1).
Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω0, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω0t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел
где
Вещественная часть формулы (8)
есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме
В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
Физ.маятник – твердое тело,которое может совершать колебания относительно неподвиж.гориз.оси не проход.через центр тяж.тела M=- mgh sin A(альфа)
Мат.маятник- матер.точка подвеш.на тонкой нерастяж.нити(невесомой)
T=2gΠ 10.Виды деформации. Закон Гука. Модуль Юнга. Деформация -это изменение формы и размера тел под действием внешних сил. Различают два вида деформаций: упругие и пластические. Упругой деформация называется, если после прекращения действия внешних сил тело принимает первоначальную форму и размеры. Пластической деформация называется, когда тело после прекращения воздействия продолжает сокращаться Закон Гука: Величина упругой деформации пропорциональна действующей силе
Модуль Юнга- численно равен сили растягивающей стержень вдвое с единичной площадью поперечного сечения. Модуль Юнга зависит от свойств материала и не зависит от размеров и формы тела Е= Уравнение Бернулли Уравнение Бернулли можно вывести, используя закон сохранения энергии при описании течения жидкости в трубке. Для элементарной струйки идеальной жидкости уравнение Бернулли записывается в виде:
Где z1 z2 – геометрическая высота или геометрический напор в произвольных сечениях 1 и 2 элементарной струйки идеальной жидкости, u2 u1 – скорость элементарной струйки в сечении 1 и 2, p1 p2 – давление в сечениях 1 и 2 элементарной струйки, p – плотность жидкости.
12.Вязкость.Закон Ньютона для вязкости. Коэффициент вязкости. Закон Стокса. Внутренним трением(или вязкостью) называется свойство жидкостей или газов оказывать сопротивление при перемещении одной части жидкости относительно другой. это свойство жидкостей и газов количественно характеризуется коэф.вязкости ῃ(или просто вязкостью) При движ.тела с сферич.формой в вязкой среде с малой скоростью на тело действует сила внутр.трения пропорц. Коэф.вязкости.
(для тел шарообразной формы, движущихся с небольшой скоростью, сила сопротивления жидкости пропорциональна вязкости жидкости, радиусу шара и скорости движения) Число Рейнольдса. Определяет режим движения жидкости.
v-скорость потока d-диаметр трубки ню-кинематический коэффициент вязкости Если 14.Основные положения молекулярно-кинетической теории (мкт). Опыты подтверждающие мкт. Основное уравнение мкт. Молекулярно- кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ. В основе молекулярно-кинетической теории лежат три основных положения:
Подтверждение: Основное уравнение мкт
15.Поверхностный слой в жидкостях. Коэф. поверхностного натяжения. Свободная энергия поверхностного слоя жидкости. Свойства вещества в этой межфазовой поверхности, толщиной в несколько поперечников атомов или молекул, отличаются от свойств внутри объёма фазы. Внутри объёма чистого вещества в твёрдом, жидком или газообразном состоянии любая молекула окружена себе подобными молекулами. В пограничном слое молекулы находятся во взаимодействии или с другим числом молекул (другим в сравнении с взаимодействием внутри объёма вещества). Это происходит, например, на границе жидкости с их паром. Среднее значение равнодействующей молекулярных сил притяжения, приложенных к молекуле, которая находится внутри жидкости, близко к нулю.
Свободная энергия поверх.слоя.жид. Эту дополнительную потенциальную энергию молекул поверхностного слоя жидкости называют свободной энергией. За счёт неё может быть произведена работа, связанная с уменьшением свободной поверхности жидкости. И, наоборот, для того, чтобы вывести молекулы, находящиеся внутри жидкости, на её поверхность, нужно преодолеть противодействие молекулярных сил, т.е. произвести работу, которая нужна для увеличения свободной энергии поверхностного слоя жидкости. При этом, изменение свободной энергии прямо пропорционально изменению площади поверхности жидкости. Так как всякая система самопроизвольно переходит в состояние, при котором её потенциальная энергия минимальна, то жидкость должна самопроизвольно переходить в такое состояние, при котором площадь её свободной поверхности имеет наименьшую величину. Например, капля дождя или тумана в воздухе приобретают форму шара, форму, соответствующую наименьшему уровню свободной энергии. Коэффициент поверхностного натяжения – это величина, характеризующая зависимость работы молекулярных сил, идущих на изменение площади свободной поверхности жидкости и самой площади изменения этой поверхности. σ = А/ΔS σ - коэффициент поверхностного натяжения А – работа молекулярных сил по изменению площади поверхности жидкости ΔS - изменение площади поверхности жидкости σ измеряется работой молекулярных сил при уменьшении площади свободной поверхности жидкости на единицу. Коэффициент поверхностного натяжения зависит от рода жидкости и внешних условий, например, температуры
16.Доп.давление под искривленной поверхностью жидкости. Формула Лапласа.
17.Смачивание и несмачивание капилярные явл.Формула Борелли-Жюрена формула Борелли-Жюрена получена в 1670 г. Величина 2а/pg,входящая в правую часть формулы,назыв.капиллярной постоянной;она явл.важной физико-хим.хар-ой жидкости. 18.Первое начало термодинамики.Изопроцессы.Работа идеал.газа при изопроцессах. Общий закон сохран.энергии с учетом процесса теплообмена и внутр.энергии имеет вид V=const A=O Q=▲U При изобарных процессах:
19.Адиабатный процесс. Уравнение Пуассона. Моляр.телоемкости при постоянных давлении и объеме. Уравнение Майера. p∙v*γ=const Графическое изображение адибатного процесса на диаграмме состояний называется адиабатой.
Сравнение между собой Ср и СV приводит к уравнению Майера:
Это уравнение показывает, что Ср больше, чем СV на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное количество теплоты на совершение работы расширения газа. Таким образом, молярная теплоемкость газа определяется лишь числом степеней свободы и не зависит от температуры. Это утверждение справедливо в довольно широком интервале температур лишь для одноатомных газов.Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависит от температуры. 20.Электрические заряды. Закон Кулона. Электрическое поле.Напряженность электрического поля. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году. Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами. Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона: Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними
Электрическое поле – вид материи с помощью которого взаимодействует электрические заряженные тела Напряженность — векторная величина. С другой стороны, сила, действующая на заряд q со стороны электрического поля, равна
21.Работа по перемещению электрического заряда в электростатическом поле. Потенциал.Эквипотенциальные поверхности Работа сил эл.пол не завсис. От траектории по которой перемещ.заряд в этом поле Поля облад.такими св-ми назыв. потенциальными. величина работы зависит от заряда его нач. и конеч. Положения и значения вектора Е на этом основании вводят понятие разности потенциала ввиде эл.напряжения 22.Постоянный электрический ток. Сила тока.Электрическое сопротивление. Закон Ома для участка цепи |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.113.44 (0.012 с.) |





 , действующую на материальную точку на две составляющие: нормальную —
, действующую на материальную точку на две составляющие: нормальную —  и касательную —
и касательную —  Нормальная составляющая силы приведёт к появлению нормального (центростремительного) ускорения:
Нормальная составляющая силы приведёт к появлению нормального (центростремительного) ускорения:  ;
;  , где r = ОА — радиус окружности.
, где r = ОА — радиус окружности. =Fl = M — момент силы, то M = Ie.
=Fl = M — момент силы, то M = Ie.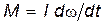 ;
;  ;
;  .
. и на косинус угла
и на косинус угла  между ними
между ними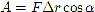





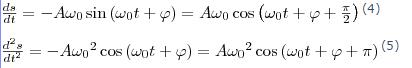




 - мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:
- мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме: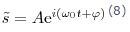

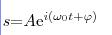
 Ftp=O
Ftp=O d=ƪ
d=ƪ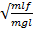

 , где К-жесткость пружины, ▲ƪ-деформация
, где К-жесткость пружины, ▲ƪ-деформация ,
, 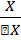


 , где
, где 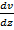 -градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.
-градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.
 – ламинарный, если
– ламинарный, если  – турбулентный режим.
– турбулентный режим. - основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи:
- основное уравнение МКТ идеального газа. Выведено в предположении, что давление газа есть результат ударов его молекул о стенки сосуда. Это же уравнение в другой записи: 

 пласа
пласа



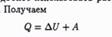 Q-все кол-во теплоты передав.сист.расходуется на совершение работы(а) и изменение внутр.сист энергии▲U.
Q-все кол-во теплоты передав.сист.расходуется на совершение работы(а) и изменение внутр.сист энергии▲U. =
= 
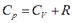 .
.
 ≈ 8,854187817·10−12 Ф/м — электрическая постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая постоянная. , действующей на помещенный в данную точку поля заряд, к этому заряду
, действующей на помещенный в данную точку поля заряд, к этому заряду  для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:
для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:  .
.





