Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы динамики Галилея-НьютонаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В основу динамики положены следующие законы (аксиомы), являющиеся обобщением практической деятельности людей и проверяемые на опыте.
Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.
Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.
Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.
где? = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.
Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J.
Теорема Гюйгенса — Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где m — полная масса тела. Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Для вывода этого закона рассмотрим простейший случай вращательного движения материальной точки. Разложим силу Касательная сила вызовет появление касательного ускорения. В соответствии со вторым законом Ньютона Ft=mat или F cos a=mat. Выразим касательное ускорение через угловое: at=re. Тогда F cos a=mre. Умножим это выражение на радиус r: Fr cos a=mr2e. Введём обозначение r cos a = l, гдеl — плечо силы, т.е. длина перпендикуляра, опущенного из оси вращения на линию действия силы. Посколькуmr2 =I — момент инерции материальной точки, а произведение
Получили основной закон динамики вращательного движения: момент силы равен произведению момента инерции на угловое ускорение. Этот закон аналогичен второму закону Ньютона Замечая, что e=dw/dt, из (4.4) получаем:
Произведение момента силы М на время её действия dt называется импульсом момента силы. Произведение момента инерции I на угловую скоростьw называется моментом импульса тела: L=Iw. Тогда основной закон динамики вращательного движения в форме можно сформулировать следующим образом: импульс момента силы равен изменению момента импульса тела. В такой формулировке этот закон аналогичен второму закону Ньютона. 7.Механическая работа. Кинетическая и потенциальная энергия. Мощность. Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения
В СИ единицей работы является джоуль (Дж). Кинетическая энергия Когда сила, приложенная к телу, больше силы сопротивления, то результирующая сила приводит тело в движение. Движущееся тело обладает кинетической энергией. Работа по ускорению тела тратится на увеличение его скорости, т.е. увеличение кинетической энергии: K = 1/2(mV2)
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.97.59 (0.011 с.) |

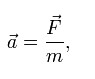
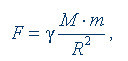
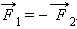
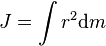



 , действующую на материальную точку на две составляющие: нормальную —
, действующую на материальную точку на две составляющие: нормальную —  и касательную —
и касательную —  Нормальная составляющая силы приведёт к появлению нормального (центростремительного) ускорения:
Нормальная составляющая силы приведёт к появлению нормального (центростремительного) ускорения:  ;
;  , где r = ОА — радиус окружности.
, где r = ОА — радиус окружности. =Fl = M — момент силы, то M = Ie.
=Fl = M — момент силы, то M = Ie.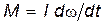 ;
;  ;
;  .
. и на косинус угла
и на косинус угла  между ними
между ними