Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Статистические методы динамики социально-экономических явленийСодержание книги
Поиск на нашем сайте 8.1. Понятие и виды ряда динамики 8.2. Основные показатели динамики и способы их расчета 8.3. Изучение сезонных колебаний 8.1. Ряд динамики представляет собой совокупность значений, характеризующих изменение изучаемого социально-экономического явления по времени. Любой ряд динамики состоит из двух элементов: временной составляющей и соответствующего значения признака (уровня) ряда динамики. В зависимости от способа представления уровней различают ряды абсолютных, относительных и средних величин. В зависимости от того представлены ли уровни ряда динамики за определенный период времени или на конкретную дату различают интервальные и моментные ряды. Ряды динамики также бывают с равноотстоящими и неравноотстоящими уровнями. 8.2. Для анализа рядов динамики определяют такие показатели, как абсолютный прирост, темп роста, темп прироста, и абсолютное значение одного процента прироста. Для проведения расчета этих показателей необходимо правильно выбрать базу сравнения. Если каждый уровень ряда динамики сравнивается с предшествующим уровнем, получают цепные показатели, если же каждый уровень ряда динамики сравнивается с одним и тем же уровнем (базой), получают базисные показатели. Выбор той или иной базы сравнения зависит от целей проведения анализа и использования его результатов. Абсолютный прирост определяют: - для цепных показателей:
- для базисных показателей:
где
Темп роста определяют: - для цепных показателей:
- для базисных показателей:
Темп прироста определяют: - для цепных показателей:
- для базисных показателей:
Темп прироста для цепных и базисных показателей может также быть определен по формуле:
Абсолютное значение одного процента прироста определяется только для цепных показателей по одной из двух формул:
В анализе рядов динамики большое внимание следует уделить расчету средних значений показателей динамики. Выбор формулы для определения среднего значения уровня ряда динамики зависит от его вида: - для интервального ряда с равноотстоящими уровнями среднее значение уровня определяется по формуле средней арифметической простой:
где - для интервального ряда с неравноотстоящими уровнями среднее значение уровня определяется по формуле средней арифметической взвешенной:
где - для моментного ряда с равноотстоящими уровнями среднее значение уровня определяется по формуле средней хронологической:
- для моментного ряда с неравноотстоящими уровнями среднее значение уровня определяется по формуле:
Средние значения определяются только для цепных показателей. Среднее значение абсолютного прироста определяется по одной из двух формул:
где Среднее значение темпа роста определяется либо по формуле средней геометрической:
где
либо по формуле:
Среднее значение темпа прироста определяется по формуле:
Пример 8.1. Произвести анализ динамики производства продукции на коммерческом предприятии за последние 6 лет (исходные данные в 1 и 2 столбцах таблицы). Спрогнозировать объем производства продукции на ближайшие три года, используя модель, построенную на основе среднего темпа роста. Решение. Результаты расчетов основных показателей динамики представлены в таблице:
Среднее значение уровня интервального ряда динамики с равно-отстоящими уровнями рассчитывается по формуле средней арифметической простой:
Средний абсолютный прирост:
Средний темп роста:
Средний темп прироста:
Прогноз объема производства продукции на ближайшие три года осуществляется с помощью модели, построенной на основе среднего темпа роста:
8.3. При анализе рядов динамики большое значение имеет изучение сезонных колебаний. Сезонные колебания представляют собой внутригодовые колебания уровней развития изучаемого социально-экономического явления. Для измерения сезонных колебаний используется специальный показатель, называемый средним индексом сезонности. Способы определения среднего индекса сезонности различны и зависят от характера основной тенденции (тренда) ряда динамики: - для ряда внутригодовой динамики, где основная тенденция развития незначительна или не наблюдается вовсе, средний индекс сезонности определяется по методу постоянной средней:
где
- для ряда внутригодовой динамики с ярко выраженной основной тенденцией развития средний индекс сезонности определяется по методу переменной средней:
где
Количество определяемых значений среднего индекса сезонности зависит от числа рассматриваемых внутригодовых периодов. Например, при квартальном представлении уровней изучаемого социально-экономичес-кого явления необходимо рассчитать четыре значения среднего индекса сезонности, а при наличии ежемесячных статистических данных − двенадцать значений среднего индекса сезонности. Исследование сезонных колебаний осуществляется в три этапа. На первом этапе выбирается метод определения среднего индекса сезонности. Критерием выбора является значение среднего темпа прироста, взятого по модулю На втором этапе реализуется процедура расчета значений среднего индекса сезонности по выбранному методу. На третьем этапе для интерпретации полученных значений среднего индекса сезонности осуществляется графическое представление полученных результатов в виде графика сезонной волны изучаемого социально-экономического явления. Пример 8.2. По данным о товарообороте группы предприятий исследовать сезонные колебания товарооборота на основе следующих исходных данных (данные в первых четырех столбцах таблицы). Решение. На первом этапе выбирается метод определения среднего индекса сезонности по значению среднего темпа прироста. Рассчитывается средний темп роста по формуле:
где
Средний темп прироста по модулю составит:
Так как модуль среднего темпа прироста меньше одного процента, то для определения среднего индекса сезонности используется метод постоянной средней. На втором этапе рассчитываются значения среднего индекса сезонности. Количество значений среднего индекса сезонности определяется числом рассматриваемых внутригодовых периодов. В данном примере число рассматриваемых внутригодовых периодов (месяцев), а значит и количество значений среднего индекса сезонности, равно двенадцать. Промежуточные расчеты приведены в таблице.
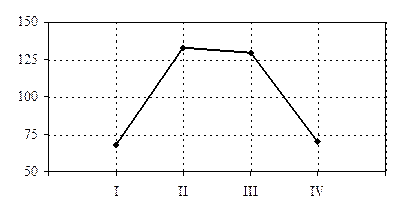
На третьем этапе по рассчитанным значениям среднего индекса сезонности строится график сезонной волны. График сезонной волны товарооборота для рассматриваемого примера будет иметь вид:
Пример 8.3. По данным о реализации продукции в магазинах города исследовать сезонные колебания (данные в первых двух столбцах таблицы). Решение. На первом этапе определяется метод расчета среднего индекса сезонности.
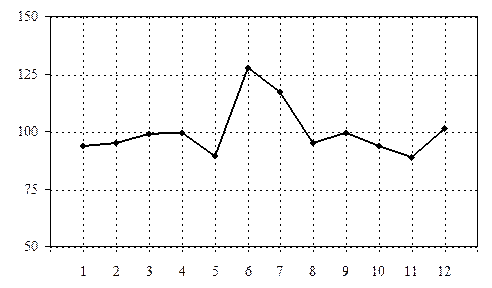
Так как модуль среднего темпа прироста больше одного процента, то для определения среднего индекса сезонности используется метод переменной средней. На втором этапе рассчитываются значения среднего индекса сезонности. Промежуточные расчеты приведены в таблице. Для нахождения выровненных значений уровней ряда динамики (столбец 6 таблицы) строится уравнение выравнивания вида:
Количество значений среднего индекса сезонности определяется числом рассматриваемых периодов. В данном примере число рассматриваемых периодов (кварталов), а значит и количество средних индексов сезонности, равно четырем.
На третьем этапе по рассчитанным значениям среднего индекса сезонности строится график сезонной волны среднедневной реализации, имеющий вид:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 ;
;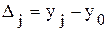 ,
,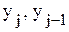 - соответственно текущее и предыдущее значение уровня;
- соответственно текущее и предыдущее значение уровня; - базисное значение уровня.
- базисное значение уровня.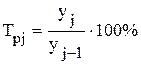 ;
; .
. ;
;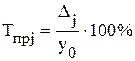 .
. .
.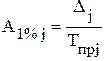 либо
либо 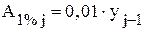 .
.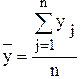 ,
,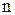 - количество уровней ряда динамики.
- количество уровней ряда динамики.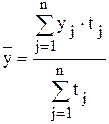 ,
,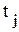 - период времени, в течение которого значение уровня не изменяется.
- период времени, в течение которого значение уровня не изменяется.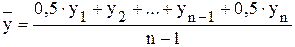 .
.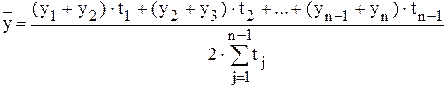 .
.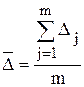 либо
либо 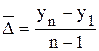 ,
, - число цепных абсолютных приростов.
- число цепных абсолютных приростов.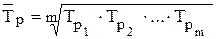 ,
, - темпа роста в долях
- темпа роста в долях .
.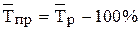 .
.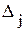 , млн.руб.
, млн.руб.
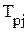 , %
, %
 , %
, %
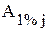 ,
млн.руб.
,
млн.руб.
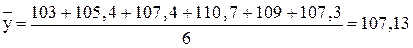 млн.руб.
млн.руб.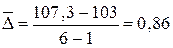 млн.руб.
млн.руб.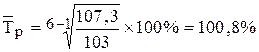 .
. .
.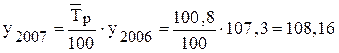 млн.руб.,
млн.руб., млн.руб.,
млн.руб.,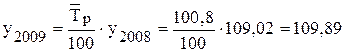 млн.руб.
млн.руб.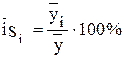 ,
,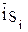 - средний индекс сезонности для i-го внутригодового периода;
- средний индекс сезонности для i-го внутригодового периода;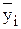 - среднее значение уровня i-го внутригодового периода;
- среднее значение уровня i-го внутригодового периода; - среднее значение уровня ряда динамики.
- среднее значение уровня ряда динамики.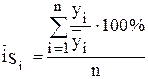 ,
,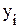 - исходные (эмпирические) значения уровней ряда динамики;
- исходные (эмпирические) значения уровней ряда динамики;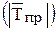 . Если
. Если  , то делается вывод о том, что основная тенденция в ряде динамики незначительна, а средний индекс сезонности определяется по методу постоянной средней. Если
, то делается вывод о том, что основная тенденция в ряде динамики незначительна, а средний индекс сезонности определяется по методу постоянной средней. Если 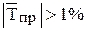 , то делается вывод о том, что основная тенденция в ряде динамики ярко выражена, а средний индекс сезонности определяется по методу переменной средней.
, то делается вывод о том, что основная тенденция в ряде динамики ярко выражена, а средний индекс сезонности определяется по методу переменной средней. ,
, - соответственно последнее и первое среднегодовые значения уровней ряда динамики.
- соответственно последнее и первое среднегодовые значения уровней ряда динамики.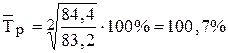 .
. ,
, 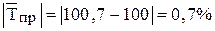 .
.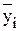
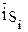
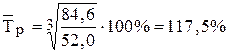 ,
, 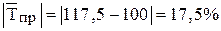 .
.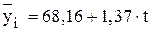 .
.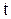


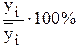
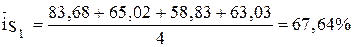 ,
,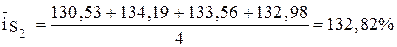 ,
,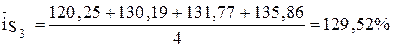 ,
,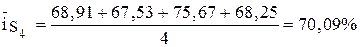 .
.