
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Используемых при статистических измерениях. Правила построения статистических показателейСодержание книги
Поиск на нашем сайте 3.1. Абсолютные и относительные статистические показатели 3.2. Понятие и виды средних величин 3.3. Структурные средние величины (мода и медиана) 3.4. Показатели вариации и способы их расчета 3.1. Статистический показатель − это количественная оценка свойства изучаемого явления. Среди статистических показателей различаются абсолютные и относительные показатели. Абсолютный показатель − это количественная величина, имеющая определенную размерность. В зависимости от целей исследования применяются натуральные и условно-натуральные, стоимостные (денежные) и трудовые единицы измерения. Относительный показатель − это результат сопоставления двух статистических показателей, который характеризует количественное соотношение между ними. Относительный показатель определяется путем деления сравниваемого (текущего) показателя на показатель, принимаемый за базу сравнения. Относительный показатель может быть получен в результате сопоставления: - одноименных статистических показателей (например, относительные показатели структуры, динамики, выполнения плана и др.); - разноименных статистических показателей (например, относительные показатели интенсивности, такие как производительность труда, фондоотдача, фондовооруженность, рентабельность и др.). На практике используются следующие виды относительных статистических показателей: 1) относительный показатель структуры (ОПС) характеризует соотношение отдельной структурной части (группы) к целому (совокупности):
где n - количество структурных частей (групп) в совокупности;
Относительный показатель структуры также называется удельным весом или долей; 2) относительный показатель координации (ОПК) характеризует соотношение между различными структурными частями (группами) одной совокупности:
где 3) относительные показатели плана (планового задания) (ОПП) характеризует соотношение между показателями, запланированным в текущем периоде и достигнутым в предыдущем периоде:
где
4) относительные показатели выполнения плана (ОПВП) характеризует соотношение между показателями, достигнутым и запланированным в текущем периоде:
где 5) относительный показатель динамики (ОПД) характеризует изменение показателя во времени и определяет направление и интенсивность его развития:
Относительный показатель динамики может быть выражен в форме коэффициента − коэффициент роста или в форме процента − темп роста. Различают относительные показатели динамики с постоянной и переменной базой сравнения. Относительные показатели динамики с постоянной базой сравнения называются базисными, а с переменной базой сравнения − цепными. Базисные показатели являются результатами сравнения текущего значения показателя с одним и тем же базисным значением. Цепные показателиявляются результатами сравнения текущего значения показателя с предыдущим значением. Произведение всех относительных показателей динамики с переменной базой сравнения равно относительному показателю динамики с постоянной базой сравнения за рассматриваемый период. Относительные показатели плана, выполнения плана и динамики связаны между собой соотношением:
6) относительный показатель интенсивности (ОПИ) характеризует соотношение различных, но связанных между собою показателей:
7) относительный показатель сравнения (ОПСр) характеризует соотношение одного и того же показателя, относящегося к разным объектам (совокупностям):
где 3.2. Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина. Средней величиной называется значение признака, наиболее характерное для изучаемой совокупности. Важным свойством средней величины является ее способность отражать то общее, что присуще всем единицам исследуемой совокупности. Значение признака в совокупности изменяется под действием множества разнообразных факторов, среди которых могут быть как основные, так и случайные. Сущность средней заключается в том, что в ней погашаются отклонения значений признака, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней величине отражать типичное значение признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам совокупности. Объективность и типичность средней величины обеспечивается при следующих условиях: 1) если средняя величина рассчитывается по массовым данным; 2) если средняя величина рассчитывается для качественно однородной совокупности, т.е. расчет средней должен сочетаться с методом группировок. В экономических исследованиях и расчетах применяют две категории средних величин: 1) степенные средние (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая); 2) структурные средние (мода и медиана). Степенные средние могут быть простыми и взвешенными. Основные расчетные формулы степенных средних величин представлены в табл. 3.1. Таблица 3.1 Основные расчетные формулы степенных средних
Использование средней арифметической простой и взвешенной и средней гармонической простой и взвешенной рассмотрим на следующих примерах. Пример 3.1. Имеются данные о выработке шести рабочих цеха за смену.
Необходимо определить среднюю выработку рабочего. Решение. Средняя выработка рабочего рассчитается как:
Обозначим через:
Данная формула получила название средней арифметической простой. Пример 3.2. По сгруппированным данным примера 3.1 определить среднюю выработку рабочего. Решение. Сгруппируем данные представленные в таблице примера 3.1. Получим дискретный ряд распределения вида:
Среднюю выработку рабочего рассчитаем как:
Обозначим через:
Данная формула получила название средней арифметической взвешенной, а Пример 3.3. На основе данных, представленных в таблице примера 3.1, определить средние затраты времени, необходимые для изготовления одной детали (среднюю трудоемкость). Решение. Затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной выработке, т.е.:
Определим трудоемкость каждого рабочего цеха:
Средние затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной средней выработке, т.е.:
Обозначим через:
Данная формула получила название средней гармонической простой. Пример 3.4. На основе сгруппированных данных, представленных в таблице примера 3.2, определить средние затраты времени, необходимые для изготовления одной детали (среднюю трудоемкость). Решение. Так как затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной выработке, то для каждой группы рабочих по выработке можно определить соответствующую трудоемкость:
Средние затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной средней выработке, т.е.:
Обозначим через:
Данная формула получила название средней гармонической взвешенной. Для определения среднего значения интервального ряда распределения по одной из рассмотренных формул в качестве величины Выбор той или иной формулы для определения средней величины зависит от экономического смысла усредняемого признака. Средней арифметической величине присущи следующие математические свойства: 1) произведение средней величины на сумму частот ряда распределения равно сумме произведений каждого значения изучаемого признака на соответствующую ему частоту:
2) сумма отклонений каждого значения изучаемого признака от средней величины равна нулю:
3) сумма квадратов отклонений каждого значения изучаемого признака от средней величины всегда меньше, чем сумма квадратов их отклонений от любой другой величины:
4) уменьшение или увеличение каждого значения изучаемого признака на одну и туже величину приводит к изменению средней на эту величину:
5) уменьшение или увеличение каждого значения изучаемого признака в одно и тоже число раза приводит к изменению средней величины в это же число раз:
6) уменьшение или увеличение частоты каждого значения изучаемого признака в одно и тоже число раз не приводит к изменению средней величины:
Для определения средней арифметической величины часто используется метод моментов (метод отсчета от условного нуля). В основе этого метода лежат математические свойства средней арифметической, согласно которым, уменьшение (увеличение) всех значений признака на одну и туже величину или уменьшение (увеличение) в одно и тоже число раз, приводит к изменению средней на эту величину или в это же число раз. Согласно методу моментов среднюю арифметическую рассчитывают по формуле:
где
Пример 3.5. По данным о выпуске продукции предприятиями отрасли (столбцы 1 и 2 таблицы) определить по методу моментов среднегодовой объем выпуска продукции. Решение. Предварительные вычисления представим в таблице, приняв
Тогда Использование метода моментов для определения средней арифметической величины позволяет значительно упростить громоздкие вычисления. При этом если частоты имеют достаточно большой общий делитель, то целесообразно их сократить на эту величину. В этом случае среднее значение не изменится. 3.3. Структурные средние величины − это величины, значения которых совпадают с определенными значениями изучаемого признака совокупности. К структурным средним величинам относятся мода и медиана. Мода − это значение признака, наиболее часто встречающегося в изучаемой совокупности. Для совокупности (дискретного ряда распределения) мода определяется визуально. Для этого просматривается совокупность (дискретный ряд распределения) и то значение признака, которое чаще всего встречается (имеет наибольшую частоту), и будет соответствовать моде. Для интервального ряда распределения сначала определяется модальный интервал (имеющий наибольшую частоту), а затем рассчитывается значение моды по формуле:
где
В случае если модальным является первый (последний) интервал, то величина Медиана − это значение признака, находящегося в середине упорядоченной совокупности. Для совокупности (дискретного ряда распределения) с нечетным количеством элементов медиане будет соответствовать значение признака, имеющего порядковый номер Для интервального ряда распределения сначала определяется медианный интервал (находящийся в середине ряда распределения), а затем рассчитывается значение медианы по одной из двух формул:
где
Для определения моды и медианы в ряде распределения с неравными интервалами целесообразно в процедуре расчета вместо частоты (частости) интервала использовать его плотность распределения. 3.4. Вариацией называется изменение значения признака в пределах изучаемой совокупности. Для осуществления вариационного анализа рассчитываются следующие основные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и коэффициент вариации. Размах вариации представляет собой максимальное значение, на которое изменяется варьирующий признак в совокупности и определяется по формуле:
где Среднее линейное отклонение − это среднее арифметическое модуля отклонения каждого значения признака от его средней величины. Определяется: - для совокупности:
- для ряда распределения:
где
Дисперсия − это среднее арифметическое квадрата отклонения каждого значения признака от его средней величины. Определяется: - для совокупности:
- для ряда распределения:
Дисперсии присущи следующие математические свойства: 1) уменьшение или увеличение каждого значения изучаемого признака на одну и туже величину не приводит к изменению дисперсии:
2) уменьшение или увеличение каждого значения изучаемого признака в А раз приводит к изменению дисперсии в А2 раз:
3) уменьшение или увеличение частоты каждого значения изучаемого признака в одно и тоже число раз не приводит к изменению дисперсии:
4) дисперсия, вычисленная от средней арифметической, всегда меньше дисперсии, вычисленной от любой другой величины, на квадрат разности между средней и этой величиной:
Приняв
где
Для расчета дисперсии часто используется метод моментов (метод отсчета от условного нуля), в основе которого лежат математические свойства дисперсии. Согласно методу моментов дисперсия рассчитывается по формуле:
где
Пример 3.6. По данным о выпуске продукции предприятиями отрасли (столбцы 1 и 2 таблицы) определить по методу моментов дисперсию ряда. Решение. Предварительные вычисления представим в таблице, приняв
Тогда Использование метода моментов для определения дисперсии позволяет значительно упростить громоздкие вычисления. При этом если частоты имеют достаточно большой общий делитель, то целесообразно их сократить на эту величину. В этом случае значение дисперсия не изменится. Среднее квадратическое отклонение определяется как квадрат-ный корень из дисперсии: - для совокупности:
- для ряда распределения:
Коэффициент вариации можно определить как отношение среднего квадратического отклонения и средней величины признака:
Чем больше значение коэффициента вариации, тем менее однородной является совокупность и тем менее точно среднее значение признака характеризует изучаемое явление. Наоборот, чем меньше значение коэффициента вариации, тем более однородной является совокупность и тем более точно среднее значение признака характеризует изучаемое явление: - если - если - если Рассмотренные показатели вариации используются для оценки уровня экономического риска. Уровень экономического риска, рассчитанный через размах вариации, среднее линейное отклонение и среднее квадратическое отношение, имеет стоимостное выражение, через коэффициент вариации, измеряется в процентах, а через дисперсию является безразмерной величиной. В любом случае, чем меньше величина рассматриваемого показателя вариации, тем ниже уровень экономического риска изучаемого экономического явления или процесса. Для оценки экономического риска рекомендуется сравнивать его уровень с размером риска за предыдущие периоды или со среднеотраслевым значением. Принято считать, что если уровень экономического риска, рассчитанный через коэффициент вариации, не превышает 25-30 %, то существует достаточно высокая вероятность получения средней (ожидаемой, запланированной) величины изучаемого признака и, наоборот. Дисперсия может быть определена с помощью правила сложения дисперсий:
где
Для использования правила сложения дисперсий соответствующим образом должна быть представлена статистическая информация. Ряд распределения должен включать группировки по двум признакам. Один из группировочных признаков является результативным, а другой − факторным. Результативный признак является результатом воздействия одной или нескольких причин и выступает в качестве основной характеристики объекта исследования. Факторный признак определяет поведение результативного и выступает в качестве причины изменения его величины. Например, объем производства продукции является результативным признаком по отношению к среднегодовой стоимости основных средств, среднему остатку оборотных средств и среднесписочной численности работников предприятия, которые выступают в качестве факторных признаков. Общая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него всех без исключения факторов (факторных признаков). Внутригрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака в пределах группы под действием на него всех факторов, кроме фактора, положенного в основание группировки:
где
Таким образом, количество внутригрупповых дисперсий определяется числом групп, выделенных по факторному признаку. Средняя из внутригрупповых дисперсий рассчитывается:
где Межгрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него фактора (факторного признака), положенного в основание группировки:
где Для определения тесноты связи между результативным (изучаемым) и факторным (положенным в основание группировки) признаками используются следующие два статистических показателя: - коэффициент детерминации:
Коэффициент детерминации изменяется в интервале от 0 до 1. Чем ближе значение показателя к единице, тем теснее связь между признаками, чем ближе к нулю, тем связь слабее. Если показатель равен единицы, связь между признаками считается функциональной, а если равен нулю, связь − отсутствует. - корреляционное отношение:
Данный показатель, в отличие от коэффициента детерминации, помимо тесноты связи определяет ее направление. Корреляционное отношение изменяется в интервале от -1 до 1. Если показатель имеет положительное значение связь считается прямой, а отрицательное − обратной. Пример 3.7. Распределение рабочих трех предприятий одного объединения по тарифным разрядам характеризуется следующими данными:
Определить: 1) дисперсию по каждому предприятию (внутригрупповые дисперсии); 2) среднюю из внутригрупповых дисперсий; 3) межгрупповую дисперсию; 4) общую дисперсию. Решение. Прежде чем приступить к решению задачи необходимо выяснить, какой признак является результативным, а какой − факторным. В рассматриваемом примере результативным признаком является «Тарифный разряд», а факторным признаком − «Номер (название) предприятия». Тогда имеем три группы (предприятия), для которых необходимо рассчитать групповую среднюю
Результаты расчета сведем в таблицу:
Средняя из внутригрупповых дисперсий рассчитаем по формуле:
Межгрупповую дисперсию определим как:
либо: тогда: Общая дисперсия будет равна: Общую дисперсию также можно рассчитать и по одной из следующих двух формул:
При решении практических задач часто приходится иметь д
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.014 с.) |

 ,
, - показатель, характеризующий i-тую структурную часть (группу) совокупности;
- показатель, характеризующий i-тую структурную часть (группу) совокупности; - показатель, характеризующий совокупность.
- показатель, характеризующий совокупность. ,
, - показатель, характеризующий структурную часть (группу) совокупности, принятую за базу сравнения;
- показатель, характеризующий структурную часть (группу) совокупности, принятую за базу сравнения; ,
, - показатель, запланированный в текущем периоде;
- показатель, запланированный в текущем периоде; - показатель, достигнутый в предыдущем периоде;
- показатель, достигнутый в предыдущем периоде; ,
, ,
, ;
; ;
;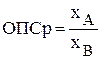 ,
, - показатели, характеризующие соответственно объекты А и В.
- показатели, характеризующие соответственно объекты А и В.

 - средняя величина изучаемого признака;
- средняя величина изучаемого признака;
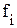 - частота (вес) i-го значения изучаемого признака.
- частота (вес) i-го значения изучаемого признака.


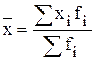





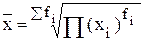



 шт./час.
шт./час.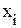 - выработку i-го рабочего;
- выработку i-го рабочего; 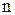 - количество рабочих в цехе;
- количество рабочих в цехе; 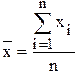 .
.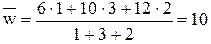 шт./час.
шт./час.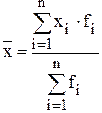 .
. .
. час/шт.
час/шт.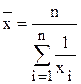 .
. час/шт.
час/шт. .
.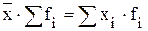 ;
;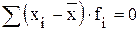 ;
; ;
;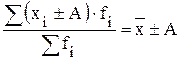 ;
;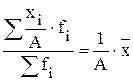 или
или 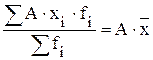 ;
; .
.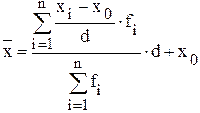 ,
, - значение признака (середина интервала), имеющего наибольшую частоту (условный нуль);
- значение признака (середина интервала), имеющего наибольшую частоту (условный нуль);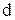 - общий множитель для всех значений признака или их отклонений от условного нуля (для ряда с равными интервалами принимается длина интервала);
- общий множитель для всех значений признака или их отклонений от условного нуля (для ряда с равными интервалами принимается длина интервала); .
.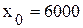 ,
, 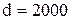 .
.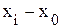

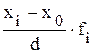
 тонн.
тонн.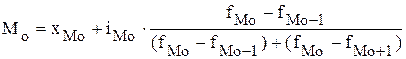 ,
,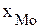 - нижняя граница модального интервала;
- нижняя граница модального интервала; - длина модального интервала;
- длина модального интервала;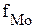 - частота модального интервала;
- частота модального интервала; - частота интервала предшествующего модальному;
- частота интервала предшествующего модальному; - частота интервала следующего за модальным.
- частота интервала следующего за модальным.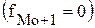 . Количество мод в совокупности (ряде распределения) может быть несколько.
. Количество мод в совокупности (ряде распределения) может быть несколько.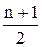 . Для совокупности (дискретного ряда распределения) с четным количеством элементов медиане будет соответствовать среднее арифметическое двух значений признака, имеющих порядковые номера
. Для совокупности (дискретного ряда распределения) с четным количеством элементов медиане будет соответствовать среднее арифметическое двух значений признака, имеющих порядковые номера 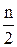 и
и 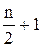 .
.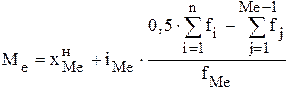 ,
, ,
,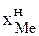 ,
,  - соответственно нижняя и верхняя границы медианного интервала;
- соответственно нижняя и верхняя границы медианного интервала; - длина медианного интервала;
- длина медианного интервала;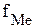 - частота медианного интервала;
- частота медианного интервала;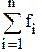 - сумма частот всех интервалов ряда распределения;
- сумма частот всех интервалов ряда распределения;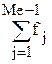 - сумма частот всех интервалов ряда распределения, предшествующих медианному.
- сумма частот всех интервалов ряда распределения, предшествующих медианному.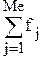 - сумма частот медианного интервала и всех ему предшествующих.
- сумма частот медианного интервала и всех ему предшествующих.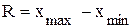 ,
, ,
, 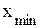 - соответственно максимальное и минимальное значения признака.
- соответственно максимальное и минимальное значения признака.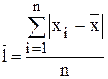 ;
;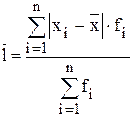 ,
,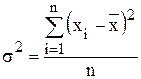 ;
;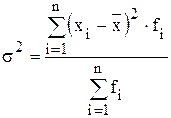 .
.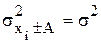 ;
;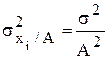 или
или  ;
; ;
; .
.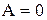 , дисперсию ряда распределения можно рассчитать как разность между средним квадратом значения признака и квадратом среднего значения признака:
, дисперсию ряда распределения можно рассчитать как разность между средним квадратом значения признака и квадратом среднего значения признака: ,
,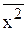 - средний квадрат значения признака, рассчитывается:
- средний квадрат значения признака, рассчитывается: или
или 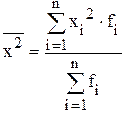 ;
; - квадрат среднего значения признака.
- квадрат среднего значения признака.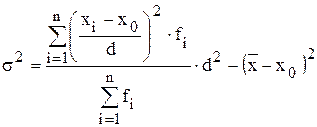 ,
, .
.
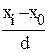

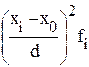

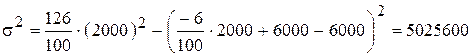 .
. ;
; .
.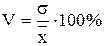 .
.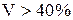 − совокупность считается неоднородной;
− совокупность считается неоднородной; − совокупность можно считать однородной;
− совокупность можно считать однородной; − совокупность считается однородной.
− совокупность считается однородной. ,
,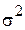 - общая дисперсия;
- общая дисперсия;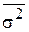 - средняя из внутригрупповых (групповых, частных) дисперсий;
- средняя из внутригрупповых (групповых, частных) дисперсий; - межгрупповая дисперсия.
- межгрупповая дисперсия.
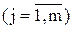 ,
, - количество выделенных групп по факторному признаку;
- количество выделенных групп по факторному признаку;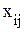 - i-тое значение результативного признака j-той группы;
- i-тое значение результативного признака j-той группы; - среднее значение результативного признака j-той группы;
- среднее значение результативного признака j-той группы;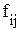 - частота i-го значения результативного признака j-той группы.
- частота i-го значения результативного признака j-той группы.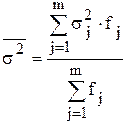 ,
, - частота (количество элементов) j-той группы.
- частота (количество элементов) j-той группы.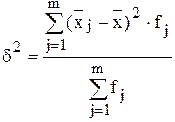 ,
, .
.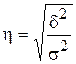 .
. и внутригрупповые дисперсии
и внутригрупповые дисперсии 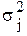 :
: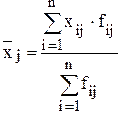
 ,
, 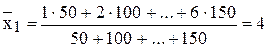 ,
,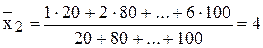 ,
, ,
,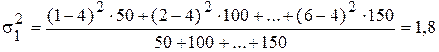 ,
, ,
, .
.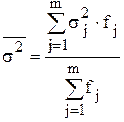
 .
. ,
, 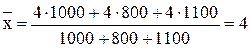
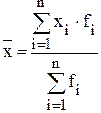 ,
,  ,
, .
.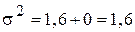 .
.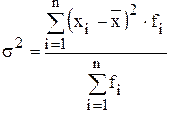

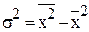
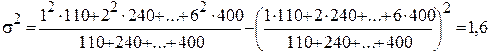 .
.


