
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидродинамика идеальной жидкости. Уравнение неразрывности потока. Уравнение БернуллиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Идеальной называется абсолютно несжимаемая жидкость, не обладающая вязкостью. Линия, касательная к каждой точке которой совпадает с направлением вектора скорости частицы жидкости в данной точке потока, называется линией тока. Совокупность линий тока, проходящих через точки бесконечно малого контура внутри потока жидкости, называется трубкой тока. Поток жидкости внутри трубки тока называется элементарной струйкой. Объем жидкости, протекающий через поперечное сечение потока за единицу времени, называется объемным расходом жидкости: dQ = dV\dT = u*dS u- скорость жидкости в произвольном сечении элементарной струйки Время (dT) за которое переместятся частицы жидкости. Следующие частицы за время (dT) заполнят пространство через поперечное сечение элементарной струйки площадью (dS) пройдет объем жидкости dV=dl*dS = u*dS*dT Реальная жидкость, в отличие от идеальной жидкости, обладает вязкостью. Свойство жидкости, которое заключается в способности жидкости оказывать сопротивление перемещению одной части жидкости относительно другой, называется внутренним трением или вязкостью.
Уравнение неразрывности жидкости. Это такое движение жидкости, при котором в её потоке не возникает пустот. Для произвольных сечений элементарной струйки с площадью dS1,dS2….dSn, где жидкость течет со скоростью соответственно u1,u2…un расход жидкости одинаков: dQ1,= dQ2…=dQn Подстановка в данное выражение позволяет получить уравнение неразрывности элементарной струйки жидкости: U1 * dS1 = u2 * dS2 = …. = un * dSn = const Для потока жидкости уравнение неразрывности имеет вид: U * S = const Уравнение Бернулли Уравнение Бернулли можно вывести, используя закон сохранения энергии при описании течения жидкости в трубке. Для элементарной струйки идеальной жидкости уравнение Бернулли записывается в виде:
Где z1 z2 – геометрическая высота или геометрический напор в произвольных сечениях 1 и 2 элементарной струйки идеальной жидкости, u2 u1 – скорость элементарной струйки в сечении 1 и 2, p1 p2 – давление в сечениях 1 и 2 элементарной струйки, p – плотность жидкости.
12.Вязкость.Закон Ньютона для вязкости. Коэффициент вязкости. Закон Стокса. Внутренним трением(или вязкостью) называется свойство жидкостей или газов оказывать сопротивление при перемещении одной части жидкости относительно другой. это свойство жидкостей и газов количественно характеризуется коэф.вязкости ῃ(или просто вязкостью) При движ.тела с сферич.формой в вязкой среде с малой скоростью на тело действует сила внутр.трения пропорц. Коэф.вязкости.
(для тел шарообразной формы, движущихся с небольшой скоростью, сила сопротивления жидкости пропорциональна вязкости жидкости, радиусу шара и скорости движения)
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.006 с.) |



 , где
, где 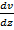 -градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.
-градиент скорости потока в данном месте,т.е быстрота изменения dz скорости направления z,перпендикулярном вектору скорости, а, следовательно, и поверхности соприкасающихся слоёв площадью S.


