
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы анализа резистивных цепей по уравнениямСодержание книги
Поиск на нашем сайте
Линейные цепи – параметры (R, L, C, M) элементов схемы замещения не зависят от величины и направления протекающих к ним напряжений. Задачи теории электрических цепей делятся на задачи анализа и задачи синтеза. Анализ – расчет электрических процессов в заданных электрических цепях, т.е. с заданной структурой и заданными характеристиками всех элементов цепи. Синтез – отыскание структуры цепи и характеристика ее элементов при которых электрический процесс в цепи будет подчиняться заданным закономерностям.
Анализ линейных электрических цепей постоянного тока Даны: величины э.д.с. и токов источников энергии их внутренние сопротивления, величины сопротивлений приемников; дана схема электрической цепи. Определить: величины токов во всех элементах цепи. Постоянный ток – неизменный по величине и по направлению. Идеальные емкостный и индуктивный элементы, а также элемент взаимоиндукции при анализе цепей постоянного тока не учитываются т.к.: сопротивление идеального индуктивного элемента постоянному току равно нулю. Идеальный емкостный элемент не пропускает постоянный ток. Цепи с одним источником питания. Метод эквивалентных преобразований Анализ основан на законе Ома и методе эквивалентных преобразований (эквивалентного сопротивления, свертки). Эквивалентное преобразование – замена группы элементов этого участка одним (или несколькими элементами с другой конфигурацией соединений) при условии, что режим работы в остальной части цепи не меняется. Алгоритм расчета 1. Путем последовательных упрощений с помощью эквивалентных преобразований рассчитывают эквивалентное сопротивление цепи. В результате получают неразветвленную электрическую цепь с одним источником и эквивалентным сопротивлением цепи. 2. Определяют ток через источник при помощи закона Ома для полной цепи
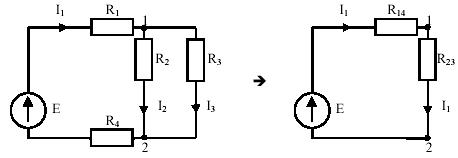
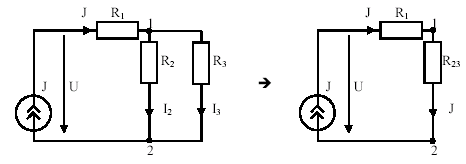
3. Используя полученное значение тока через источник питания определяют токи во всех ветвях цепи. 4. Для проверки правильности расчета цепи составляют энергетический баланс цепи (или строят потенциальную диаграмму для любого контура). Примечание. 1. Если цепь питается от источника тока, то расчет ведут по п.3, 4. 2. В случае сложно разветвленной цепи необходимо воспользоваться эквивалентным преобразованием: ÑÞΥ и YÞÑ. Преобразование YÞÑ
Преобразование ÑÞΥ
Пример 1
Проверка:
Пример 2
Проверка:
Пример 3
Используется преобразование звезда – треугольник YÞÑ.
Цепи с несколькими источниками питания В основе расчета лежат законы Кирхгофа, принцип наложения, теорема об эквивалентном генераторе, принцип взаимности. Методы расчета, основанные на применении законов Кирхгофа и их модификации (метод контурных токов, метод узловых напряжений) – методы общего анализа цепей (определяются токи во всех ветвях). Методы наложения, эквивалентного генератора, взаимности – методы частичного анализа (определяется ток в одной ветви).
Метод непосредственно применения законов Кирхгофа Алгоритм расчета 1. Выбирают произвольное положительное направление искомых токов в ветвях и обозначают их на схеме. Число неизвестных токов равно числу всех ветвей схемы без учета ветвей содержащих источники тока, т.к. токи в ветвях, содержащих источники тока, известны – (в – вит).

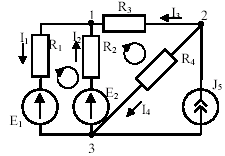
2. Составляют уравнение по 1-му закону Кирхгофа для (y-1) узлов схемы, с учетом токов от источников тока, где y – число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно совпало бы с уравнением, полученным при суммировании уже составленных уравнений для предыдущих узлов (т.е. линейно-независимых уравнений – (y-1)). При составлении уравнений следуют правилу: если ток выходит из узла, то его записывают со знаком (+), если входит – то со знаком (-). В рассматриваемом примере: +I1 – I2 – I3 = 0 (для узла 1); -I1 + I2 –I4+J = 0 (для узла 3). 3. Составляют [(в - вит) - (у - 1)] уравнений по 2 закону Кирхгофа для независимых контуров. 3.1. Выбирают независимые контуры. а) Их число равно [(в - вит) - (у - 1)]; б) Независимый контур – контур, в который входит хотя бы одна новая ветвь, не вошедшая в предыдущие контуры. Эффективно использовать метод ячеек, по которому каждый независимый контур – это ячейка сети (рыбацкой) – внутри отсутствуют ветви. в) При выборе контуров ветви с источником тока исключаются (в противном случае при составлении уравнений в них вошли бы бесконечно большие слагаемые и они не имели бы смысла (E=∞; R=∞)). 3.2. Выбирают положительное направление обхода контуров (обычно по часовой стрелке).
3.3. При составлении уравнений следуют правилу: если направление тока и э.д.с. на элементе совпадает с направлением обхода, то падение напряжения и э.д.с. записывают со знаком (+), если не совпадает, то со знаком (–). В рассматриваемом примере: -I1R1 – I2R2. = E1 - E2. (для независимого контура E1® R1® R2®E2); +I2R2-I3R3 + I4R4 = E2 (для независимого контура E2® R2® R3® R4). 4. Решают тем или иным методом полученную систему линейных алгебраических уравнений. В рассматриваемом примере: 5. На основании полученного решения проставляют на схеме реальное положительное направление токов в ветвях. 6. Проверяют правильность полученного решения с помощью энергобаланса или (и) потенциальной диаграммы:
В рассматриваемом примере: Метод контурных токов Метод основан на введении промежуточной неизвестной величины – контурного тока и использовании 2 закона Кирхгофа. Контурный ток – собственный ток каждого независимого контура. Реальный ток в ветвях определяется как алгебраическая сумма соответствующих контурных токов. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа, т.е. числу независимых контуров [(в - вит) - (у - 1)]. Алгоритм расчета (после вывода расчетных уравнений по 2 закону Кирхгофа): 1. Проставляют направления контурных токов на расчетной схеме. Для единообразия в знаках сопротивлений все контурные токи направляют в одну и туже сторону (например, по часовой стрелке).
2. Для каждого независимого контура (ячейки) составляют расчетное контурное уравнение согласно правилу: левая часть равна сумме произведений контурного тока на собственное сопротивление этого контура, взятое со знаком плюс, и контурных токов прилегающих контуров на сопротивления смежных ветвей, взятых со знаком минус: правая часть равна алгебраической сумме э.д.с. этого контура – контурной э.д.с. Примечание: При наличии ветвей с источниками тока либо источники тока преобразуют в эквивалентные источники э.д.с.; либо рассматривают контурный ток контура, в который входит ветвь с источником тока, как известный и равный току этого источника тока. Уравнения составляют лишь для контуров с неизвестными контурными токами. Напряжение на элементе от тока источника тока записывается в правой части уравнения со знаком (+), если направление обхода совпадает с направлением этого контурного тока (противоположно направлению этого тока на элементе). В рассматриваемом примере: 3. Решают тем или иным методом полученную систему линейных алгебраических уравнений. 4. На основании полученного решения определяют величину и направление реальных токов в ветвях, для чего: - в расчетной схеме изменяют на противоположное направление контурного тока полученного со знаком минус; - в ветвях внешнего контура расчетной схемы найденный контурный ток является действительным током ветви; - в смежных ветвях реальный ток ветви определяют алгебраической суммой контурных токов смежных контуров, в том числе и от источников токов: при этом направление тока в ветви совпадает по направлению с общим по величине контурным током. В рассматриваемом примере: I1 = -I11; I2 = -I11 + I22; I3 = -I22; I4 = I22 + J. 5. Рисуют электрическую цепь с положительными направлениями сил тока в ветвях. 6. Проверяют правильность полученного решения с помощью энергобаланса или (и) потенциальной диаграммы.
Метод узловых потенциалов Метод основан на введении промежуточной неизвестной величины – потенциала узла и использовании 1-го закона Кирхгофа. Если будут известны потенциалы узлов схемы, то ток в любой ветви можно найти по закону Ома для участка цепи, содержащего э.д.с., т.к. любая точка схемы может быть заземлена без изменения токораспределения в ней (т.е. её потенциал можно принять равным нулю). В этом случае число неизвестных составляет (y-1) (т.е. равно числу независимых уравнений по 1-му закону Кирхгофа). Алгоритм расчета (после вывода расчетных уравнений по 1-му закону Кирхгофа): 1. Принимают потенциал одного из узлов равным 0.
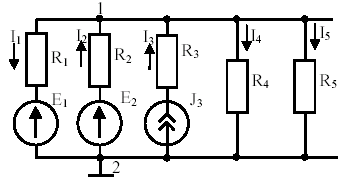
2. Составляют уравнение для каждого из оставшихся (y-1) узлов согласно правилу: левая часть уравнения равна сумме произведений потенциала рассматриваемого узла на сумму проводимостей всех ветвей, сходящихся в этом узле, взятое со знаком плюс, и потенциалов остальных узлов на сумму проводимостей ветвей, соединяющих эти узлы с рассматриваемым узлом, взятые со знаком минус; правая часть уравнения равна алгебраической сумме произведений э.д.с. ветвей, сходящихся в рассматриваемом узле на проводимости этих ветвей (так называемый узловой ток рассматриваемого узла). При этом произведения берутся со знаком плюс, если э.д.с. направлены к рассматриваемому узлу. Примечание При наличии ветвей с источником тока необходимо учесть следующее: - проводимость ветви с источником тока равна нулю; - в правую часть уравнения добавляется алгебраическая сумма токов от источников тока в ветвях, сходящихся в рассматриваемом узле. При этом ток источника тока берется со знаком плюс, если он направлен к рассматриваемому узлу. В рассматриваемом примере:
3. Решают тем или иным способом полученную систему линейных алгебраических уравнений. 4. На основании полученного решения определяют величину и направление токов в ветвях по закону Ома для участка цепи, содержащего э.д.с. В рассматриваемом примере: 5. Проверяют правильность полученного решения с помощью баланса мощностей или (и) потенциальной диаграммы.
Метод двух узлов
Этот метод является частным случаем метода узловых потенциалов.
Алгоритм расчета 1. Принимают потенциал одного из узлов равным нулю. Проставляют условно-положительные направления напряжения между узлами и токов в ветвях. 2. Определяют величину и реальное положительное направление напряжения между узлами по формуле
При этом узловые токи ΣEkGk и ΣJk берутся со знаком плюс, если э.д.с. и ток источника тока направлены к узлу с условно взятым большим потенциалом. 3. Определяют величины и направления токов в ветвях по закону Ома для участка цепи, содержащего э.д.с. 4. Рисуют электрическую цепь с положительными направлениями сил тока в ветвях. 5. Проверяют правильность полученного решения с помощью энергобаланса или (и) потенциальной диаграммы.
Замена нескольких параллельных ветвей с источниками на одну эквивалентную
Использую формулу для определения напряжения между 2-мя узлами получают
где действует правило знаков: если э.д.с. и ток источника тока направлены к узлу с большим потенциалом, то берут (+), если нет, то (–). При этом
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.107 (0.008 с.) |

 .
.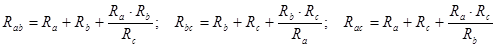







 .
.
 (для контуров E1 ® R1 ® R2 ® E2 и E2 ®R2 ® R3 ®R4).
(для контуров E1 ® R1 ® R2 ® E2 и E2 ®R2 ® R3 ®R4).
 (для узлов 1 и 2).
(для узлов 1 и 2).
 .
.





