
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение мкт газовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m 0, концентрацией молекул n, средним значением квадрата скорости Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема. Вопрос №20 Универса́льная га́зовая постоя́нная (также — постоянная Менделеева) — термин, впервые введённый в употребление Д. Менделеевым в 1874 г. Численно равна работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К. В Международной системе единиц (СИ) универсальная газовая постоянная равна[3] R = 8,3144598(48) Дж⁄(моль∙К). Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеМенделеева — Клапейрона) — формула, устанавливающая зависимость между давлением,молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
где · · · · Так как
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. Вопрос №21 Число соударений молекул, происходящих в единицу времени, зависит от скорости движения молекул и пропорционально концентрации реагирующих веществ, поскольку от концентрации зависит расстояние между молекулами. В силу этого число соударений в единицу времени увеличивается при увеличении температуры и давления в системе. Длина свободного пробега молекулы — это среднее расстояние (обозначаемое Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры. Формула
Вопрос №22 Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν +d ν, т. е.
откуда
Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:
Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0 ν 2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν 2, то функция f(ν), начинаясь от нуля, достигает максимума при ν B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно ν B.
Рис.1
Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки
Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν):
Вопрос №23 Не найден Вопрос №24 Первый закон термодинамики -Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил. Основные понятия термодинамики- Система - тело или группа тел, находящихся во взаимодействии и мысленно обособляемых от окружающей среды. Изолированные системы - это системы, имеющие постоянный объем, через границы которых не происходит обмена веществом или анергией с окружающей средой. Работа- упорядоченная форма передачи энергии, а теплота является неупорядоченной формой ее передачи. Внутренняя энергия- общий запас энергии системы, включая энергию: поступательного и вращательного движения молекул; внутримолекулярного колебательного движения атомов и атомных групп, составляющих молекулы; вращения электронов в атоме; ядер атомов и т. д., но без учета кинетической энергии тела в целом и его потенциальной энергии положения Термодинамика - один из важнейших разделов физики и физической химии, предметом изучения которого являются: А) основные соотношения, позволяющие рассчитать количество выделенного или поглощенного тепла в физических и химических превращениях и совершаемую при этом работу; Б) выявление возможного самопроизвольного течения процессов в определенном направлении, их равновесие. Вопрос №25 Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяемая отношением бесконечно малогоколичества теплоты δ Q, полученного телом, к соответствующему приращению его температуры δ T [1]:
Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/К. ДЖОУЛЯ ЗАКОН — внутренняя энергия идеального газа зависит только от температуры и не зависит от его плотности (объема) Уравнение майера Для любого идеального газа справедливо соотношение Майера:
где Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарическому процессу видеальном газе:
в рассматриваемом случае:
Очевидно, уравнение Майера показывает, что различие теплоемкостей газа равно работе, совершаемойодним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальнойгазовой постоянной R — механический эквивалент теплоты. 2. СПОСОБЫ ИЗМЕРЕНИЯ ТЕПЛОЕМКОСТИ Вопрос №26 Процесс наз.обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходноечерез ту же последовательность промежут. состояний, что и в прямом процессе, но проходимую в обратномпорядке. Необратимые процессы могут протекать самопроизвольно только в одном направлении; таковы диффузия,теплопроводность, вязкое течение и др. Для хим. р-ции применяют понятия термодинамич. и кинетич.обратимости, к-рые совпадают только в непосредств. близости к состоянию равновесия. Равновесные это такие процессы, при которых система переходит последовательно из одного состояния равновесия в другое. Под системой равновесия термодинамической системы понимается такое состояние, к которому она стремится, принимая при этом минимальные значения общей энергии. В состоянии равновесия параметры системы при отсутствии внешнего воздействия остаются постоянными. Неравновесные это такие процессы, которые не сопровождаются состоянием равновесия. Для этих процессов характерно, что различные части системы имеют различные термодинамические параметры. Равновесное состояние является предельным случаем неравновесного состояния, если скорость стремится к нулю. Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется. ИЗОБАРНЫЙ ПРОЦЕСС ( ИЗОХОРНЫЙ ПРОЦЕСС ( ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ( Вопрос № 27 адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётсяравновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Физический смысл адиабатического процесса[править | править вики-текст] Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии[5], то адиабатический процесс в силу отсутствия теплообмена (
где Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит[8]:
Здесь Уравнение Пуассона Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением[6][15][16]
где
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
где
Поскольку Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении ( Уравнение:
где
индексы Политро́пный процесс, политропи́ческий процесс — термодинамический процесс, во время которого удельная теплоёмкость газаостаётся неизменной. Вопрос №28 Тепловая машина — устройство, преобразующее тепловуюэнергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник).Преобразование осуществляется за счет изменения внутренней энергии рабочего тела — на практикеобычно пара или газа. Идеальная тепловая машина — машина в которой произведенная работа и разница между количествомподведенного и отведенного тепла равны. Цикл Карно́ — идеальный термодинамический цикл. Тепловаямашина Карно, работающая по этому циклу, обладает максимальным КПД извсех машин, у которых максимальная и минимальная температурыосуществляемого цикла совпадают соответственно с максимальной иминимальной температурами цикла Карно. Состоит из 2 адиабатических и 2изотермических процессов. Одним из важных свойств цикла Карно является его обратимость: он можетбыть проведён как в прямом, так и в обратном направлении, при этомэнтропия адиабатически изолированной (без теплообмена с окружающейсредой) системы не меняется. Цикл Карно состоит из четырёх стадий: 1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру 2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника 3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру 4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
КПД тепловой машины Карно[править | править вики-текст] Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
КПД реальной тепловой машины значительно меньше так как значительная часть энергии теряется. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов, которые могут происходить в термодинамических системах. Существуют несколько эквивалентных формулировок второго закона термодинамики: · Постулат Клаузиуса: «Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому» [1] (такой процесс называется процессом Клаузиуса). · Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара» (такой процесс называется процессом Томсона). Вопрос №29 Рассмотрим обратимый процесс по пути 1а2 и 2б1. Т.к. процессе 1а2б1 обратимый, то для него справедливо равенство Клаузиуса
Разобьем этот интеграл на два: по пути 1а2 и 2б1
Поменяем пределы интегрирования второго интеграла
Таким образом, сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса.
Неравенство Клаузиуса (1854): Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено (приведённое количество теплоты), неположительно.
Термодинамическая энтропия энтропия представляет собой однозначную функцию состояния рабочего тела, принимающую для каждого его состояния определенное значение. Из сказанного следует, что энтропия есть функция любой пары параметров, т.е. s = f1(p, ); s = f2(, т); s = f3(p, т). Таким образом, энтропия принадлежит к той же группе величин, что и внутренняя энергия и энтальпия, т.е. величина изменения энтропии в процессе определяется только начальным и конечным состоянием рабочего тела и не зависит от характера процесса. Другими словами, энтропия является параметром состояния и, следовательно, изменение энтропии в циклах равно нулю.
Э не́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическомизотермическом процессе равна работе, совершённой системой над внешними телами. Определение Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так: · Отсюда дифференциал свободной энергии равен: · Видно, что это выражение является полным дифференциалом относительно независимых переменных Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так: · где В соответствии с рекомендациями ИЮПАК энергию Гельмгольца в химической термодинамике можно также обозначать как A [1]. Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц. Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении. Энтропия и вероятность Увеличение энтропии системы означает переход в состояние, имеющее большую вероятность. Если S – энтропия, w – вероятность термодинамического состояния,
то
Термодинамическая вероятность состояния w определяет число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. Согласно определению Обычно интерес представляет только изменение энтропии. При переходе из состояния 1, которому отвечает вероятность w 1, в состояние 2, энтропия изменяется от S 1до S 2. Тогда из формулы (9.43) следует
Тепловая смерть Вселенной — гипотеза, выдвинутая Р. Клаузиусом как экстраполяция второго начала термодинамики на всюВселенную. По мысли Клаузиуса, Вселенная должна прийти в состояние термодинамического равновесия, или «тепловой смерти»[1] (термин, описывающий конечное состояние любой замкнутой термодинамической системы). При этом все виды энергии должны перейти в тепловую энергию. Термодинамика рассматривает систему, находящуюся в состоянии тепловой смерти, как систему, в которой термодинамическая энтропия максимальна. Статистический характер второго закона термодинамики приводит к заключению, что увеличение энтропии в самопроизвольных процессах указывает на наиболее вероятные пути развития процессов в изолированной системе. Невозможность процесса следует понимать лишь как его малую вероятность по сравнению с обратным. Поэтому второй закон термодинамики в отличие от первого нужно рассматривать как закон вероятности. Он тем точнее соблюдается, чем больше размеры системы. Для систем, состоящих из громадного числа частиц, наиболее вероятное направление процесса практически является абсолютно неизбежным, а процессы, самопроизвольно выводящие систему из состояния равновесия, практически невозможны. Так, самопроизвольное изменение плотности 1 см3 воздуха в атмосфере с отклонением на 1 % от ее нормальной величины может происходить лишь один раз за 3 - Ю32 лет. Однако для малых количеств вещества флуктуации плотности отнюдь не невероятны, а наоборот, вполне закономерны. Для объема воздуха 1 10 - 6 см3 повторяемость однопроцентных флуктуации плотности составляет всего 10 11 с. Вопрос №31 Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближениитемпературы к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных. Третье начало термодинамики может быть сформулировано так: «Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».
или
где Межмолекулярные силы (intermolecular forces), силы, действующие между соседними молекулами. В отличие от газов в жидкостях и твердых телах М.с. не дают молекулам разлететься в пространстве. Однако они слабее ковалентных связей, и при нагреве в-ва их действие легко преодолевается. Одним из видов М.с. являются силы Ван-дер-Ваальса, обусловленные неоднородным распределением электронов в молекуле в каждый отд. момент времени: мгновенные электрич. диполи индуцируют возникновение диполей в соседних молекулах. Эти объекты слабо притягиваются друг к другу. Примером в-ва, в к-ром действуют только подобные силы, служит азот. Если молекулы в-ва обладают постоянным дипольным моментом (напр., хлористый водород), то диполь-дипольное взаимодействие превышает силы Ван-дер-Ваальса и как бы маскирует последние. Самым сильным видом межмол. взаимодействия является водородная связь, свойственная, напр., молекуле воды (H2O). Отклонение газов Закон Бойля-Мариотта следует из кинетической теории газов, если принять, что размеры молекул пренебрежимо малы по сравнению с расстоянием между ними и отсутствует межмолекулярное взаимодействие. Иными словами, Закон Бойля-Мариотта выполняется строго дляидеального газа. Для реальных газов, у которых влиянием размеров молекул и их взаимодействием пренебрегать нельзя, закон Бойля-Мариотта выполняется приближённо, тем лучше, чем дальше от критического состояния находится газ. При больших давлениях необходимо вводить поправки на силы притяжения между молекулами и на объем самих молекул. Как и уравнение Клайперона, закон Бойля — Мариотта описывает предельный случай поведения реального газа, более точно описываемый уравнением Ван-дер-Ваальса. Вопрос №32 Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основныетермодинамические величины в модели газа Ван-дер-Ваальса. Уравнение состояния Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где · · · · Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка Для
где · Критическое состояние 1) предельное состояние равновесия двухфазных систем, вкотором обе сосуществующие фазы (См. Фаза) становятся тождественными по своим свойствам; 2) состояние вещества в точках фазовых переходов (См. Фазовый переход) II рода. К. с., являющеесяпредельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесиижидкость — газ, а в растворах — при фазовых равновесиях (См. Фазовое равновесие) газ — газ, жидкость —жидкость, жидкость — газ, твёрдое тело — твёрдое тело. На диаграммах состояния (См. Диаграммасостояния) К. с. соответствуют предельные точки на кривых равновесия фаз (рис. 1, а и б) — т. н.критические точки (См. Критическая точка).Согласно фаз правилу (См. Фаз правило) критическая точкаизолирована в случае двухфазного равновесия чистого вещества, а, например, в случае бинарных (двойных)растворов (См. Растворы) критические точки образуют критическую кривую в пространстветермодинамических переменных (параметров состояния). Значения параметров состояния,соответствующие К. с., называются критическими — критическое давление рк , критическая температура Тк ,критический объём Vк , критический состав хк и т. д. Вопрос №33 Испаре́ние — процесс фазового перехода вещества из жидкого состояния в парообразное или газообразное, происходящий на поверхности вещества. Плавле́ние — это процесс перехода тела из кристаллического твёрдого состояния в жидкое, то есть переход вещества из одного агрегатного состояния в другое. Кипе́ние — процесс интенсивного парообразования, который происходит в жидкости, как на свободной её поверхности, так и внутри её структуры. При этом в объёме жидкости возникают границы разделения фаз, то есть на стенках сосуда образуются пузырьки, которые содержат воздух и насыщенный пар. Кристаллиза́ц |
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 950; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |


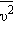 и средней кинетической энергией
и средней кинетической энергией  поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов. ,
, — давление,
— давление, — молярный объём,
— молярный объём, — универсальная газовая постоянная
— универсальная газовая постоянная — абсолютная температура, К.
— абсолютная температура, К. , где
, где  — количество вещества, а
— количество вещества, а  , где
, где  — масса,
— масса,  — молярная масса, уравнение состояния можно записать:
— молярная масса, уравнение состояния можно записать:
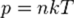 где
где  — концентрация атомов,
— концентрация атомов,  — постоянная Больцмана.
— постоянная Больцмана.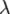 ), которое частица пролетает за время свободного пробега от одного столкновения до следующего.
), которое частица пролетает за время свободного пробега от одного столкновения до следующего. , где
, где  — эффективное сечение молекулы,
— эффективное сечение молекулы,  — концентрация молекул.
— концентрация молекул.

 (1)
(1)
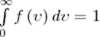



 ,
, — универсальная газовая постоянная,
— универсальная газовая постоянная,  — молярная теплоемкость при постоянном давлении,
— молярная теплоемкость при постоянном давлении,  — молярная теплоемкость при постоянном объёме.
— молярная теплоемкость при постоянном объёме.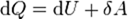 ,
,
 .
.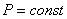 )
)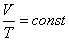 или
или  .
. )
) или
или 
 )
) или
или  .
. Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Серьёзное исследование адиабатических процессов началось в XVIII веке[1].  ) системы со средой сводится только к последним двум процессам[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид[7][Комм 1]
) системы со средой сводится только к последним двум процессам[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид[7][Комм 1]
 — изменение внутренней энергии тела,
— изменение внутренней энергии тела, 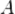 — работа, совершаемая системой.
— работа, совершаемая системой.
 — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла[8].
— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла[8]. 
 — его объём,
— его объём,  — показатель адиабаты,
— показатель адиабаты,  и
и  — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме. 

 всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении
всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении  ) газ нагревается (
) газ нагревается ( возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент
возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент  ) к теплоёмкости при постоянном объёме (
) к теплоёмкости при постоянном объёме (  (гамма) или
(гамма) или  (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква
(каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинская буква  [1].
[1]. ,
, — теплоёмкость газа,
— теплоёмкость газа, — удельная теплоёмкость (отношение теплоёмкости к единице массы) газа,
— удельная теплоёмкость (отношение теплоёмкости к единице массы) газа, и
и  обозначают условие постоянства давления или постоянства объёма, соответственно.
обозначают условие постоянства давления или постоянства объёма, соответственно. , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты
, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты  . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает. , тело совершает механическую работу, а энтропия остаётся постоянной.
, тело совершает механическую работу, а энтропия остаётся постоянной. . Над телом совершается работа, его энтропия уменьшается.
. Над телом совершается работа, его энтропия уменьшается.
 .
. .
. .
.

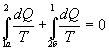



 , часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической(расчёт равновесий химических реакций).
, часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической(расчёт равновесий химических реакций). , где
, где  — внутренняя энергия,
— внутренняя энергия,  .
. .
. ,
, — химический потенциал, а
— химический потенциал, а  — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция
— число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция  .
. Дж/К – постоянная Больцмана,
Дж/К – постоянная Больцмана,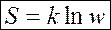 – формула Больцмана. (9.43)
– формула Больцмана. (9.43) , т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя
, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя  !). Возрастание энтропии, что следует из второго начала термодинамики, означает переход системы из менее вероятных в более вероятные состояния.
!). Возрастание энтропии, что следует из второго начала термодинамики, означает переход системы из менее вероятных в более вероятные состояния. . (9.44)
. (9.44)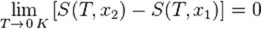

 — любой термодинамический параметр.
— любой термодинамический параметр.
 — молярный объём,
— молярный объём, учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка  — объем молекул газа.
— объем молекул газа. молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
молей газа Ван-дер-Ваальса уравнение состояния выглядит так:



