
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения молекулярно-кинетической теорииСодержание книги
Поиск на нашем сайте
1. Все вещества состоят из мельчайших частиц - атомов и молекул. 2. Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается. 3. Молекулы вещества взаимодействуют между собой с силами притяжения F пр и отталкивания F от.
r = r 0 , F от = F пр, r < r 0 , F от > F пр, r > r 0 , F от < F пр, r ® ¥, F ® 0. Характер движения молекул зависит от агрегатного состояния вещества. Движение молекул газов сводится к хаотическому поступательному движению. Скорость молекул газов зависит от температуры.
4.8. Термодинамические параметры - температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины: На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна Учитывая, что Для любой массы m газа, т.е. для любого числа киломолей
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества Второе начало термодинамики утверждает, что все необратимые процессы (а такими являются практически все тепловые процессы, во всяком случае, все естественно протекающие процессы) идут так, что энтропия участвующих в них тел возрастает, стремясь к максимальному значению. Максимальное значение энтропии достигается тогда, когда система приходит в равновесное состояние. Вместе с тем выше уже отмечалось, что переход к равновесному состоянию является значительно более вероятным по сравнению со всеми другими переходами. Поэтому и наблюдаются только те изменения состояния, при которых система переходит из менее вероятного в более вероятное состояние (термодинамическая вероятность возрастает). Связь между термодинамической вероятностью состояния системы и ее энтропией была установлена в 1875 г. двумя знаменитыми учеными – Д. Гиббсом и Л. Больцманом. Эта связь выражается формулой Больцмана, которая имеет вид:
где
4.9. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеМенделеева — Клапейрона) — формула, устанавливающая зависимость междудавлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
где
Так как
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия Уравнение состояния Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка Для
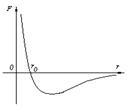
Изотерма линия на диаграмме состояния, изображающая процесс, происходящий при постоянной температуре (изотермический процесс). Уравнение Изотерма идеального газа pV = const, где р — давление, V — объём газа. Для реального газа уравнение Изотерма имеет более сложный характер и переходит в уравнение Изотерма идеального газа только при малых давлениях или высоких температурах. На рис. 2.8 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.
На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма Критические параметры
Поскольку весь процесс происходит при постоянной температуре T, кривую, что изображает зависимость давления р от объёма V, называют изотермой. При объёме V1 начинается конденсация газа, а при объёме V2 она заканчивается. Если V > V1 то вещество будет в газообразном состоянии, а при V < V2 — в жидком. Опыты показывают, что такой вид имеют изотермы и всех других газов, если их температура не очень высокая. В этом процессе, когда газ превращается в жидкость при изменении его объёма от V1 к V2, давление газа остаётся постоянным. Каждой точке прямолинейной части изотермы 1—2 соответствует равновесие между газообразным и жидким состояниями вещества. Это означает, что при определённых T и V количество жидкости и газа над ней остаётся неизменным. Равновесие имеет динамический характер: количество молекул, которые покидают жидкости, в среднем равняется количеству молекул, которые переходят из газа в жидкость за одно и то же время. Также существует такое понятие как критическая температура, если газ находится при температуре выше критической (индивидуальна для каждого газа, например для углекислого газа примерно 304 К), то его уже невозможно превратить в жидкость, какое бы давление к нему не прилагалось. Данное явление возникает вследствие того, что при критической температуре силы поверхностного натяжения жидкости равны нулю. Если продолжать медленно сжимать газ при температуре большей критической, то после достижения им объёма, равного приблизительно четырем собственным объёмам молекул, составляющих газ, сжимаемость газа начинает резко падать.
4.10. Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход. Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
Эта формула является математическим выражением первого начала термодинамики Для квазистатических процессов выполняется следующее соотношение:
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.007 с.) |

 , где р — давление идеального газа, m0 — масса молекулы,
, где р — давление идеального газа, m0 — масса молекулы,  среднее значение концентрация молекул, квадрата скорости молекул.
среднее значение концентрация молекул, квадрата скорости молекул. получим основное уравнение МКТ идеального газа в виде:
получим основное уравнение МКТ идеального газа в виде: 
 . Так как в одном киломоле содержится
. Так как в одном киломоле содержится  молекул, то внутренняя энергия одного киломоля газа будет
молекул, то внутренняя энергия одного киломоля газа будет 
 , получим
, получим 
 внутренняя энергия
внутренняя энергия

 ,
,
 , R – универсальная газовая постоянная, NA – число Авогадро.
, R – универсальная газовая постоянная, NA – число Авогадро.
 — давление,
— давление, — молярный объём,
— молярный объём, — универсальная газовая постоянная
— универсальная газовая постоянная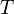 — абсолютная температура,К.
— абсолютная температура,К. , где
, где  — количество вещества, а
— количество вещества, а  , где
, где 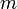 — масса,
— масса,  —молярная масса, уравнение состояния можно записать:
—молярная масса, уравнение состояния можно записать:


 — закон Бойля — Мариотта (изотрмический процесс)
— закон Бойля — Мариотта (изотрмический процесс) — Закон Гей-Люссака (изобарический).
— Закон Гей-Люссака (изобарический). — закон Шарля (второй закон Гей-Люссака, 1808 г., изохорический)
— закон Шарля (второй закон Гей-Люссака, 1808 г., изохорический) становится функцией не только температуры, но и объёма.
становится функцией не только температуры, но и объёма.
 — молярный объём,
— молярный объём, учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка  — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).
— силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).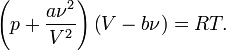 Где
Где  Рис. 2.8.Изотермы газа Ван-дер-Ваальса
Рис. 2.8.Изотермы газа Ван-дер-Ваальса
 при одинаковых значениях параметров
при одинаковых значениях параметров  и
и  . При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения
. При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения  ,
,  и
и  в этой точке называются критическими параметрами. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями
в этой точке называются критическими параметрами. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями  .
. можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба. Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами
можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба. Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами  Изотермы реального газа (схематично)
Изотермы реального газа (схематично) где
где — подведённая к телу теплота, измеренная в джоулях
— подведённая к телу теплота, измеренная в джоулях ] — работа, совершаемая телом против внешних сил, измеренная в джоулях
] — работа, совершаемая телом против внешних сил, измеренная в джоулях где
где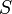 — энтропия, измеренная в джоулях/кельвин
— энтропия, измеренная в джоулях/кельвин — химический потенциал
— химический потенциал — количество частиц в системе
— количество частиц в системе


