
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамическое определение энтропииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла
Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся изменением тепла, вследствие изменения структуры. Рудольф Клаузиус дал величине Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
где Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия). Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю. Второй закон термодинамики исключает возможность создания вечного двигателя второго рода. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона. 1 — Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе. Это явление называют рассеиванием или диссипацией энергии. Приведем второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (1865): Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния 2 — Постулат Кельвина. Процесс, при котором работа переходит в теплоту без каких-либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.
4.14. При нарушении равновесия система стремится вернуться в равновесное состояние. Мы ограничимся рассмотрением явлений, возникающих в газах в тех случаях, когда отклонения от равновесия невелики. При нарушениях равновесия в телах возникают потоки тепла, либо массы, электрического заряда и т.п. В связи с этим соответствующие процессы носят название явлений переноса. Причиной любого явления переноса является наличие градиента некоторой физической величины. Теплопроводность газов Рассмотрим газ, в котором каким-то способом поддерживается непостоянство температуры вдоль направления, которое мы обозначим буквой x. Представим мысленно площадку площадью S, перпендикулярную к этому направлению. В этом случае через площадку S возникает поток тепла, величина которого определяется формулой:
Вычислим поток тепла в газе, основываясь на молекулярно-кинетических представлениях. Если температура газа в разных точках различна, то и средняя энергия молекул в этих точках также будет различной. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят запасённую ими энергию. Этот перенос энергии и обуславливает процесс теплопроводности в газах. Исходя из упрощённых представлений, будем считать, что количество молекул, пролетающих через площадку S за секунду, равно
Каждая молекула несёт с собой энергию, соответствующую температуре в том месте, где произошло последнее соударение её с другой молекулой. Молекулам, летящим вдоль оси х, следует приписать энергию
отвечающую температуре в плоскости (х-l), а молекулам, летящим в противоположном направлении, - энергию
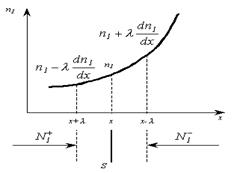
отвечающую температуре в плоскости (х + l), где х – координата плоскости S (см. рис.). Тогда количество энергии, переносимое молекулами за секунду через площадку S в положительном направлении оси х, можно записать следующим образом:
Сравнивая полученное выражение с законом Фурье, получим выражение для коэффициента теплопроводности через молекулярно-кинетические параметры газа:
Диффузия в газах Предположим, что в единице объёма двухкомпонентной газовой смеси содержится n1 молекул одного вида и n2 молекул другого вида. Полное число молекул в единице объёма равно n = n1 + n2. Допустим, что в направлении оси х создаются градиенты концентраций В этом случае газодинамических потоков не возникает. Однако вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах. Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением
где ri = nimi – парциальная плотность i – ой компоненты. Эти формулы представляют собой эмпирические уравнения диффузии. Их называют уравнением Фика.
Получим уравнение диффузии, основываясь на молекулярно-кинетических представлениях, причём для упрощения расчётов будем считать, что молекулы обеих компонент мало отличаются друг от друга по массе (m1» m2» m) и имеют практически одинаковые эффективные диаметры (d1» d2» d). В этом случае молекулам обеих компонент можно приписывать одинаковую среднюю скорость теплового движения < u >, а среднюю длину свободного пробега вычислить по формуле Пусть изменение концентрации первой компоненты вдоль оси х даётся функцией n1 = n1 (x). Поток молекул первой компоненты летящих через поверхность S в положительном направлении оси х, равен
а соответствующий поток молекул первой компоненты, летящих в отрицательном направлении оси х равен разности этих потоков
Таким образом, мы пришли к уравнению диффузии Фика, причём получили для коэффициента диффузии выражение
Вязкость газов Сила трения между двумя слоями жидкости может быть вычислена по формуле
где h- коэффициент вязкости, Согласно второму закону Ньютона, взаимодействие двух слоёв с силой F можно рассматривать как процесс, в ходе которого от одного слоя к другому передаётся в единицу времени импульс, по величине равный F. Поэтому уравнение вязкости можно представить в виде
где К - импульс, передаваемый за секунду от слоя к слою через поверхность S. Следовательно, величину К можно рассматривать как поток импульса через поверхность S. Знак минус в этой формуле обусловлен тем обстоятельством, что импульс “течёт” в направлении убывания скорости u.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

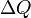 к величине абсолютной температуры
к величине абсолютной температуры 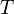 (то есть тепло, переданное системе, при постоянной температуре):
(то есть тепло, переданное системе, при постоянной температуре):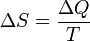 .
.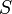 имя «энтропия», происходящее от греческого слова «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.
имя «энтропия», происходящее от греческого слова «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию. ,
,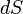 — приращение (дифференциал) энтропии некоторой системы, а
— приращение (дифференциал) энтропии некоторой системы, а 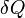 — бесконечно малое количество теплоты, полученное этой системой.
— бесконечно малое количество теплоты, полученное этой системой.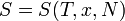 , называемая энтропией, такая, что ее полный дифференциал
, называемая энтропией, такая, что ее полный дифференциал  .
.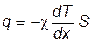 ,где
,где 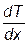 - градиент температуры, т.е. величина, показывающая, как быстро изменяется температура в направлении оси х, c (каппа) – коэффициент пропорциональности, зависящий от свойств среды и называемый коэффициентом теплопроводности. Знак минус в формуле отражает то обстоятельство, что тепло течёт в направлении убывания температуры. Эта формула называется уравнением теплопроводности или законом Фурье.
- градиент температуры, т.е. величина, показывающая, как быстро изменяется температура в направлении оси х, c (каппа) – коэффициент пропорциональности, зависящий от свойств среды и называемый коэффициентом теплопроводности. Знак минус в формуле отражает то обстоятельство, что тепло течёт в направлении убывания температуры. Эта формула называется уравнением теплопроводности или законом Фурье.
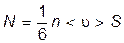 .
.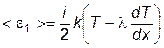 ,
,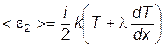 ,
,
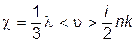 .
.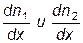 , причём
, причём  . Тогда,
. Тогда,  , так что n, а, следовательно, и Р постоянны (в силу Р = nkT).
, так что n, а, следовательно, и Р постоянны (в силу Р = nkT).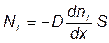 ,где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Знак минус указывает на то, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i – го вида mi, получим выражение для потока массы i – ой компоненты:
,где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Знак минус указывает на то, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i – го вида mi, получим выражение для потока массы i – ой компоненты: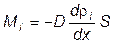 ,
,
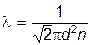 , где n = n1 + n2.
, где n = n1 + n2. ,
,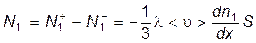 .
.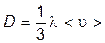 .
. ,
, - градиент скорости, т.е. величина, показывающая, как быстро изменяется скорость жидкости или газа в направлении х, перпендикулярном к направлению движения слоёв, S – величина поверхности, по которой действует сила F. Это уравнение и есть эмпирическое уравнение вязкости.
- градиент скорости, т.е. величина, показывающая, как быстро изменяется скорость жидкости или газа в направлении х, перпендикулярном к направлению движения слоёв, S – величина поверхности, по которой действует сила F. Это уравнение и есть эмпирическое уравнение вязкости.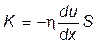 ,
,


