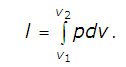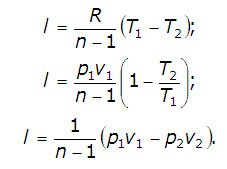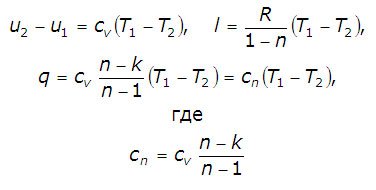Второй закон термодинамики. Энтропия, третий закон термодинамики.

Второй закон термодинамики. Энтропия.

Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.

Существует два классических определения второго закона термодинамики:

· Кельвина и Планка

Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

· Клаузиуса

Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Второй закон связан с понятием энтропии (S).

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

· 100% энергии не может быть преобразовано в работу

· Энтропия может вырабатываться, но не может быть уничтожена

Третий закон термодинамики

1. Первый и второй законы термодинамики не позволяют определить значение S0 энтропии системы при абсолютном нуле температуры (T = 0°К). В связи с этим оказывается невозможным теоретический расчет абсолютных значений энтропии,изохорно-изотермного и изобарно-изотермного потенциалов системы, а также константы равновесия.
2. На основании обобщения экспериментальных исследований свойств различных веществ при сверхнизких температурах был установлен закон, устранивший указанную трудность и получивший название принципа Нернста или третьего закона термодинамики. В формулировке Нернста он гласит: в любом изотермическом процессе, проведенном при абсолютном нуле температуры, изменение энтропии системы равно нулю, т. е.
DS (T=0) = 0, S = S0 = const,

независимо от изменения любых других параметров состояния (например, объема, давления, напряженности внешнего силового поля и т. д.). Иными словами, при абсолютном нуле температуры изотермический процесс является также и изоэнтропийным.
3. Из третьего закона термодинамики следует, что для всех тел при T = 0°К обращаются в нуль теплоемкости Сp и СV и термодинамический коэффициент расширяемости a. Из него также вытекает вывод о невозможности осуществления такого процесса, в результате которого тело охладилось бы до температуры T = 0°К (принцип недостижимости абсолютного нуля температуры).
4. Принцип Нернста был развит Планком, предположившим, что S0 = 0: при абсолютном нуле температуры энтропия системы равна нулю. Физическое истолкование принципа Нернста в формулировке Планка дается в статистической физике.
Условие S0 = 0 при T = 0°К является следствием квантового характера процессов, происходящих в любой системе при низких температурах, и выполняется только для систем находящихся при Т = 0°К в состоянии устойчивого, а не метастабильного равновесия. На основании гипотезы Планка можно определить абсолютные значения энтропии системы в произвольном равновесном состоянии.

 

Обратимые и необратимые термодинамические процессы.

1. Обратимым термодинамическим процессом называется термодинамический процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность.

2. Необратимым термодинамическим процессом называется термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы.

3. Всякий необратимый процесс в одном направлений (прямом) протекает самопроизвольно, а для осуществления его в обратном направлении так, чтобы система вернулась в первоначальное состояние, требуется компенсирующий процесс во внешних телах, в результате которого состояния этих тел оказываются отличными от первоначальных. Например, процесс выравнивания температур двух соприкасающихся различно нагретых тел идет самопроизвольно, т. е. не связан с необходимостью одновременного существования каких-либо процессов в других (внешних), телах. Однако для осуществления обратного процесса увеличения разности температур тел до первоначальной нужны компенсирующие процессы во внешних телах, обусловливающие, например, работу холодильной машины.

 

Основные термодинамические процессы идеальных газов.

Основными процессами в термодинамике являются:

§ изохорный, протекающий при постоянном объеме;

§ изобарный, протекающий при постоянном давлении;

§ изотермический, происходящий при постоянной температуре;

§ адиабатный, при котором теплообмен с окружающей средой отсутствует;

§ политропный, удовлетворяющий уравнению pvⁿ = const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

§ уравнение процесса в p—v и T—s координатах;

§ связь между параметрами состояния газа;

§ изменение внутренней энергии;

§ величину внешней работы;

§ количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

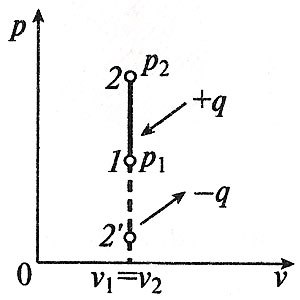
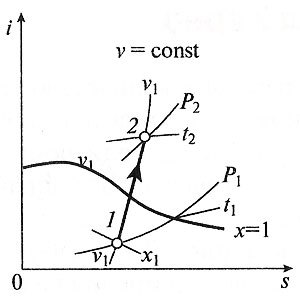
Изохорный процесс вp,v—,T,s— иi,s-координатах (диаграммах)

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

p/T = R/v = const,

т. е. давление газа прямо пропорционально его абсолютной температуре:

p₂/p₁ = T₂/T₁.

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δ v = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

q = c_v(T₂— T₁).

Т. к. l = 0, то на основании первого закона термодинамики Δ u = q, а значит изменение внутренней энергии можно определить по формуле:

Δ u = c_v(T₂— T₁).

Изменение энтропии в изохорном процессе определяется по формуле:

s₂– s₁ = Δ s = c_v ln(p₂/p₁) = c_v ln(T₂/T₁).

Изобарный процесс

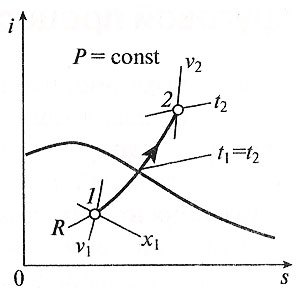
Изобарный процесс вp,v—,T,s— иi,s-координатах (диаграммах)

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

v/T = R/p = const

или

v₂/v₁ = T₂/T₁,

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

l = p (v₂–v₁).

Т. к. pv₁ = RT₁ и pv₂ = RT₂, то

l = R (T₂– T₁).

Количество теплоты при c_p = const определяется по формуле:

q = c_p (T₂– T₁).

Изменение энтропии будет равно:

s₂– s₁ = Δ s = c_p ln(T₂/T₁).

Изотермический процесс

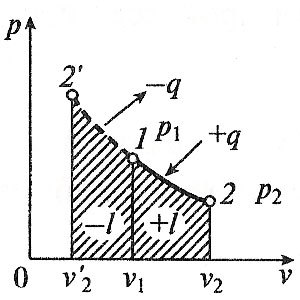
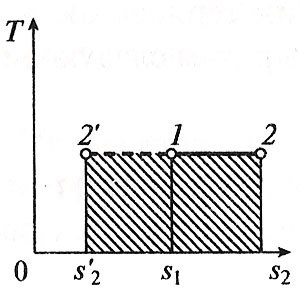
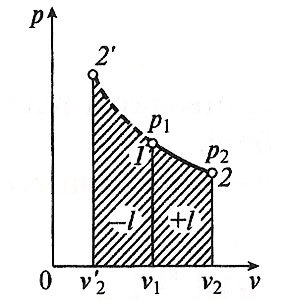
Изотермический процесс вp,v—,T,s— иi,s-координатах (диаграммах)

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

pv = RT = const

или

p₂/p₁ = v₁/v₂,

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

l = RT ln (v₂– v₁) = RT ln (p₁– p₂).

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δ u = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

q = l.

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

s₂– s₁ = Δ s = R ln(p₁/p₂) = R ln(v₂/v₁).

Адиабатный процесс

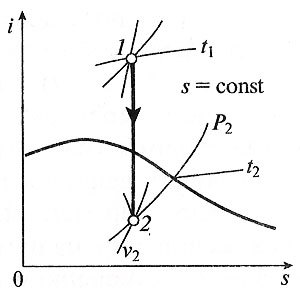
Адиабатный процесс вp,v—,T,s— иi,s-координатах (диаграммах)

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как d q = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

d u + p d v = 0

или

Δ u + l = 0,

следовательно

Δ u = — l.

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c _ад, и условие d q = 0 выразим следующим образом:

d q = c _адd T = 0.

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c _ад = 0).

Известно, что

с_p/c_v = k

и уравнение кривой адиабатного процесса (адиабаты) в p,v -диаграмме имеет вид:

pv^k = const.

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

Значения показателя адиабаты k для некоторых газов:

k _{воздуха} = 1,4

k _{перегретого пара} = 1,3

k _{выхлопных газов ДВС} = 1,33

k _{насыщенного влажного пара} = 1,135

Из предыдущих формул следует:

l = — Δ u = c_v (T₁–T₂);

i₁–i₂ = c_p (T₁–T₂).

Техническая работа адиабатного процесса (l _техн) равна разности энтальпий начала и конца процесса (i₁–i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T,s -диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае d s > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

pvⁿ = const.

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p,v и T в любых двух точках на политропе:

p₂/p₁ = (v₁/v₂)ⁿ; T₂/T₁ = (v₁/v₂)^n-1; T₂/T₁ = (p₂/p₁)^(n-1)/n.

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

q = (u₂– u₁) + l.

Поскольку

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p,v координатах в зависимости от показателя политропа n.

pv⁰ = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p⁰v = const, p^1/∞v = const, pv^∞ = const – изохора;

pv^k = const (n = k) – адиабата.

n> 0 – гиперболические кривые,

n< 0 – параболы.