
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренняя энергия, внешняя работа, первый закон термодинамики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
НиТД 1. Основные параметры технической термодинамики. Определения. Параметр – это один из совокупности независимых физических величин, определяющих тепловое состояние системы (тела). Например, если системой является водяной пар, то для определения состояния этой системы используются параметры состояния: давление, объем, масса, температура и другие. Параметры состояния всегда относятся к термодинамическим системам, которые находятся в термодинамическом равновесии. Термодинамическое равновесное состояние – это состояние термодинамической системы, характеризующееся при постоянных внешних условиях неизменностью параметров во времени и отсутствия в системе потоков. Число параметров состояния, которое необходимо для однозначного определения равновесного состояния, зависит от вида термодинамической системы. Состояние простой системы (отсутствуют электрические, магнитные и др. эффекты) будет однозначно определено двумя, либо тремя параметрами состояния. В технической термодинамике основными параметрами состояния являются термические параметры: абсолютное давление (р), температура (Т) и удельный объем (v). Давление – сила, действующая нормально к площади. p = F/f (1.1) где F – сила, действующая нормально к площади; f – площадь. В международной системе единиц (СИ) имеет размерность p = 1Н/1м2 = 1 Па. Паскаль равен давлению, вызываемому силой 1н по нормали к поверхности в 1 м2. Все технические приборы, измеряющие давление, показывают избыточное давление Ризб. Избыточное давление – это разность между давлением в термодинамической системе (абсолютное давление) и внешним атмосферным давлением В. Термодинамика оперирует только с абсолютным давлением в термодинамической системе, которое равно Pабс = Ризб + В, (1.2) Рабс = В – Рвак (1.3) где Ризб – избыточное давление; B – атмосферное давление; Рабс – абсолютное давление; Рвак – величина вакуума (разряжения) формулы (1.2) используется при давлениях больше атмосферного, а формула (1.3) – при давлениях меньше атмосферного. В технической термодинамике часто используют внесистемные единицы давления. Из них весьма распространена единица «физическая атмосфера» (атм) 1 атм = 1,01325·105 Па, техническая атмосфера (ат)
1 ат = 9·80665·104 Па и бара 1 бар = 1·105 Па. Температура – одна из основных величин в технической термодинамике. Принцип измерения температуры основан на очевидном законе логики. Если два тела в отдельности находятся в тепловом равновесии с третьим телом, то все три тела находятся в тепловом равновесии, а значит имеют одинаковую температуру. Следовательно, по показанию термометра можно сравнить температуру разных тел. Для измерения температуры используют технические приборы: термометры, термопары, термометры сопротивления и др. В каждом из этих приборов используется зависимость какого-либо физического свойства (коэффициента объемного расширения, удельного сопротивления, электродвижущей силы) от температуры. Определение температуры при помощи таких приборов зависит от индивидуальных свойств термодинамического вещества (чувствительного элемента термометра), так как одна и та же физическая величина имеет разную зависимость от температуры для различных материалов. Абсолютная температура (не зависит от свойств термометрического вещества) определяется с помощью идеального газового термометра, что следует из Второго закона термодинамики. Это впервые показал Кельвин и в его честь эта абсолютная (термодинамическая температура) была названа температурой Кельвина. Термодинамическая температура по Второму закону не может иметь отрицательных значений, а нулевая точка равна наинизшей термодинамически возможной температуре – абсолютному нулю. Измерение термодинамической температуры газовым термометром сложно и дорого. Поэтому используют простой метод измерения температур, результаты которых по возможности приближались к значениям термодинамической температуры. Поэтому, кроме термодинамической шкалы температур существует молекулярная температурная шкала (МТШ-90). Единицей измерения температуры в Международной системе единиц (СИ) является градус Кельвина – К, как по термодинамической шкале температур, так и по МТШ-90. Между температурой по термодинамической шкале, выраженной в градусах Кельвина и в градусах Цельсия имеется связь: Т, К = t˚C + 273,15 (1.4) Кроме МТШ-90 в ряде стран используют другие температурные шкалы – шкала Фаренгейта, шкала Реомюра, шкала Ренкина. Ниже приведены соотношения для пересчета значений температур из одних шкал в другие.
Т, К = t˚ C + 273,15; (1.5) t, ˚ F = 1,8 t˚ C + 32; (1.6) t, ˚ R = 0,8 t˚ C; (1.7) t, ˚ Ra = 1,8 (t˚ C + 273,15), (1.8) где Т К – термодинамическая температура по шкале Кельвина, К; t˚ C – температура по шкале Цельсия, ˚ C; t˚ F – температура по шкале Фаренгейта, ˚ F; t˚ R – температура по шкале Реомюра, ˚ R; t˚ Ra– температура по шкале Ренкина, ˚ Ra. Удельный объем, как температура и давление, являются термодинамическим параметром. Удельный объем (v) – величина, равная отношению объем V однородного тела к его массе: v = V/m = 1/ρ (1.9) Размерность удельного объема в Международной системе СИ (м3/кг). Эта величина обратно пропорциональна плотности (ρ). В термодинамике удобно рассматривать не плотность, а удельный объем, так как многие термодинамические системы имеют настоящую массу и тогда удельный объем пропорционален общему объему. В термодинамике широко распространено понятие о количестве вещества «n». Во времена Ньютона количество вещества отождествлялось с массой. В современной метрологии количеством вещества называется число атомов, молекул, ионов или, как говорят, число структурных элементов, из которых состоит вещество. Но число частиц тела макроскопических размеров велико (N ≈ 1025). Поэтому вводится величина пропорциональная числу частиц, которая получила название количества вещетсва. n = N/Na, (1.10) где Na – универсальная газовая постоянная или число Авогадро. Количество вещества относится к категории основных в системе СИ и получила наименование моля при следующем определении: моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится в углероде-12 массой 0,012 кг. Из формулы (1.10) видно, что число Авогадро выражает число молекул или других частиц, содержащихся в одном моле вещества. Масса вещества естественно будет пропорциональна количеству вещества n m = M·n, (1.11) где М – молярная масса вещества. Подставляя в формулу значения количества вещества, получим: M = m·Na/N, (1.12) Молярная масса вещества М пропорциональна относительной молекулярной массе данного вещества и может быть определена из соотношения: М = k·Mr, (1.13) где k – размерный коэффициент пропорциональности, зависящий от системы единиц и равный k = 10-3 кг/моль (в системе СИ). Относительная молекулярная масса Mr определяется по формуле: Mr = Σ liAr,i, (1.14) где li – число атомов i-го элемента в молекуле, Ar,i– относительная атомная масса i-го элемента (безразмерная величина). Заметим, что значение молярной массы, выраженной г/моль или кг/кмоль, численно совпадает с относительной молекулярной массой.
Теплоемкость и энтальпия. Энтальпия h = u + Рv, как любой параметр состояния, может быть определена через любую пару независимых параметрами состояния. Выразим полный дифференциал энтальпии, используя при его определении в качестве независимых термических параметров Р и Т
Для изобарного процесса при Р=const, используя первый закон термодинамики, получим выражение
в соответствии с которым, изобарная теплоемкость определяется как
Применив уравнение (4.47) к (4.46) получим выражение для определения элементарного изменения энтальпии реальных веществ
Для энтальпии идеального газа, подчиняющегося уравнению Pv=RT, будет выполняться равенство
т.е. энтальпия идеальных газов не зависит от давления, а выражение (4.48) для идеальных газов примет вид
Поскольку изобарная теплоемкость идеальных газов величиа постоянная, то энтальпия идеальных газов есть функция только температуры. В свою очередь, для изобарной теплоемкости идеального газа не зависимо от процесса справедливо выражение
Абсолютное значение энтальпии можно получить интегрированием выражения (4.48). При этом, необходимо выбрать начало ее отсчета, приняв h0 при фиксированных параметрах газа РО и ТО.
Необходимо помнить, что начало отсчета энтальпии и внутренней энергии связаны соотношением
в соответствии с которым, приняв uО=0, получим hО = PОvО, т.е. начало отсчета энтальпии будет больше нуля. При различных значениях РО и ТО будут различными и абсолютные значения энтальпии. Однако в расчетах процессов используется разница энтальпий, а не их абсолютные значения. Для разницы энтальпий процесса выбор параметров начала отсчета энтальпии никакой роли не играет
Прокомментируем расчет абсолютного значения энтальпии на примере идеального газа. Примем начало отсчета энтальпии идеального газа hО при 0 ОС. Приняв при 0 ОС uО=0, получим hО=uО+PОvО=RTО=273,15R, тогда абсолютное значение энтальпии вычисляется по формуле
Приняв начало отсчета энтальпии и внутренней энергии идеального газа от абсолютного нуля ТО=0 К, и задав uО=0, получим hО=PОvО=RTО=0R=0, т.е. в данном случае численные значения начала отсчета внутренней энергии и энтальпии одинаковы и равны нулю. Расчетное выражение абсолютной энтальпии в этом случае будет представлено в виде
Абсолютные значения энтальпий по выражениям (4.55) и (4.56) при одинаковых температурах будут разные, но разница энтальпий в одинаковом интервале температур будет одинаковой
Таким образом, в расчетах абсолютного значения энтальпии основным требованием является необходимость выбора одинаковых параметров для принятия начала отсчета внутренней энергии и энтальпии. Для идеального газа начало отсчета энтальпии и внутренней энергии фиксируется только температурой. При расчете разности энтальпий выбор параметров начала отсчета энтальпии никакой роли не играет. Поэтому, если сразу расчитывается разность энтальпий (выражение 4.55), то параметры начала отсчета энтальпии вообще не нужны, если разница энтальпий определяется через их абсолютные значения h2-h1, то они должны иметь одинаковые (любые) параметры начала их отсчета.
Теплоемкость тела — это физическая величина, определяемая отношением количества теплоты, поглощенной телом при нагревании, к изменению его температуры: Физический смысл теплоемкости тела: теплоемкость тела равна количеству теплоты, поглощенному телом при нагревании или выделенному при его охлаждении на 1К. Теплоемкость тела — это произведение удельной теплоемкости вещества, из которого оно изготовлено, и массы этого тела: C = cт. Удельная теплоемкость — это способность разных веществ к поглощению теплоты при их нагревании. Молярная теплоемкость — это физическая величина, равная отношению количества теплоты, поглощенного веществом при нагревании или выделенного при охлаждении, к количеству молей нем и изменению температуры: Физический смысл молярной теплоемкости: молярная теплоемкость вещества, определяемая количеством теплоты, которое поглощается при нагревании или выделяется при охлаждении 1 моля вещества на 1 К. что говорит о том, что молярная теплоемкость не зависит от его химического состава и температуры. Уравнение Роберта Майера: молярная теплоемкость идеального газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной: Закон Дюлонга и Пти: молярная теплоемкость всех теплоемкостей должна быть одинакова и равна утроенной универсальной газовой постоянной:
Третий закон термодинамики 1. Первый и второй законы термодинамики не позволяют определить значение S0 энтропии системы при абсолютном нуле температуры (T = 0°К). В связи с этим оказывается невозможным теоретический расчет абсолютных значений энтропии,изохорно-изотермного и изобарно-изотермного потенциалов системы, а также константы равновесия. независимо от изменения любых других параметров состояния (например, объема, давления, напряженности внешнего силового поля и т. д.). Иными словами, при абсолютном нуле температуры изотермический процесс является также и изоэнтропийным.
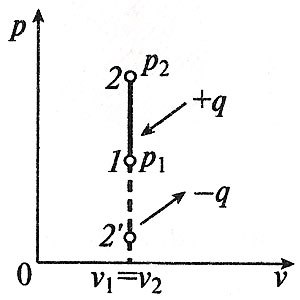
Изохорный процесс
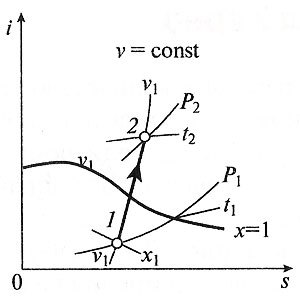
Изохорный процесс вp,v—,T,s— иi,s-координатах (диаграммах) При изохорном процессе выполняется условие v = const. Из уравнения состояния идеального газа (pv = RT) следует: p/T = R/v = const, т. е. давление газа прямо пропорционально его абсолютной температуре: p2/p1 = T2/T1. Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δ v = const). Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле: q = cv(T2— T1). Т. к. l = 0, то на основании первого закона термодинамики Δ u = q, а значит изменение внутренней энергии можно определить по формуле: Δ u = cv(T2— T1). Изменение энтропии в изохорном процессе определяется по формуле: s2– s1 = Δ s = cv ln(p2/p1) = cv ln(T2/T1). Изобарный процесс
Изобарный процесс вp,v—,T,s— иi,s-координатах (диаграммах) Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует: v/T = R/p = const или v2/v1 = T2/T1, т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре. Работа будет равна: l = p (v2–v1). Т. к. pv1 = RT1 и pv2 = RT2, то l = R (T2– T1). Количество теплоты при cp = const определяется по формуле: q = cp (T2– T1). Изменение энтропии будет равно: s2– s1 = Δ s = cp ln(T2/T1). Изотермический процесс
Изотермический процесс вp,v—,T,s— иi,s-координатах (диаграммах) При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно: pv = RT = const или p2/p1 = v1/v2, т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается. Работа процесса будет равна: l = RT ln (v2– v1) = RT ln (p1– p2). Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δ u = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения: q = l. При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе. Изменение энтропии равно: s2– s1 = Δ s = R ln(p1/p2) = R ln(v2/v1). Адиабатный процесс
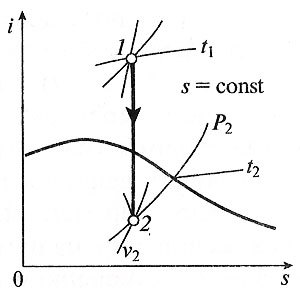
Адиабатный процесс вp,v—,T,s— иi,s-координатах (диаграммах) Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как d q = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид: d u + p d v = 0 или Δ u + l = 0, следовательно Δ u = — l. В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа. Обозначим теплоемкость в адиабатном процессе через c ад, и условие d q = 0 выразим следующим образом: d q = c адd T = 0. Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c ад = 0). Известно, что сp/cv = k и уравнение кривой адиабатного процесса (адиабаты) в p,v -диаграмме имеет вид: pvk = const. В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона). Значения показателя адиабаты k для некоторых газов: k воздуха = 1,4 k перегретого пара = 1,3 k выхлопных газов ДВС = 1,33 k насыщенного влажного пара = 1,135 Из предыдущих формул следует: l = — Δ u = cv (T1–T2); i1–i2 = cp (T1–T2). Техническая работа адиабатного процесса (l техн) равна разности энтальпий начала и конца процесса (i1–i2). Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T,s -диаграмме он изображается вертикальной линией. Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае d s > 0, и процесс называется реальным адиабатным процессом. Политропный процесс Политропным называется процесс, который описывается уравнением: pvn = const. Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной. Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p,v и T в любых двух точках на политропе: p2/p1 = (v1/v2)n; T2/T1 = (v1/v2)n-1; T2/T1 = (p2/p1)(n-1)/n. Работа расширения газа в политропном процессе равна:
В случае идеального газа эту формулу можно преобразовать:
Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики: q = (u2– u1) + l. Поскольку
представляет собой теплоемкость идеального газа в политропном процессе. При cv, k и n = const cn = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью. Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов. Графическое представление политропа в p,v координатах в зависимости от показателя политропа n.
pv0 = const (n = 0) – изобара; pv = const (n = 1) – изотерма; p0v = const, p1/∞v = const, pv∞ = const – изохора; pvk = const (n = k) – адиабата. n> 0 – гиперболические кривые, n< 0 – параболы. Теплофикационный цикл. В условиях развитого хозяйства экономически особенно целесообразно вырабатывать электрическую энергию и тепло комбинированным способом в одной теплосиловой установке, называющейся теплоэлектроцентралью. В так называемых конденсационных установках, рассмотренных ранее и вырабатывающих только механическую (или электрическую) энергию, весь отработавший пар конденсируется охлаждающей циркуляционной водой. Последняя нагревается обычно до 15—30° С и уносит с собой огромное количество тепла, которое не может быть использовано вследствие низкой температуры воды. Эти потери с охлаждающей водой составляют в конденсационных установках до 60% тепла, выделяющегося при сгорании топлива
Стремление к использованию тепла, уносимого циркуляционной (охлаждающей) водой, привело к мысли значительно повысить ее температуру за счет повышения давления отработавшего пара и использовать ее для отопления зданий, технологических процессов самых разнообразных производств, сушки, варки и т. п. Таким образом осуществляется комбинированная выработка электрической и тепловой энергии. Такие установки называют теплофикационными или теплоэлектроцентралями (ТЭЦ). Комбинированная выработка электрической и тепловой энергии является основой теплофикации, получившей особое развитие как наиболее передовой и совершенный метод производства тепловой и электрической энергии.
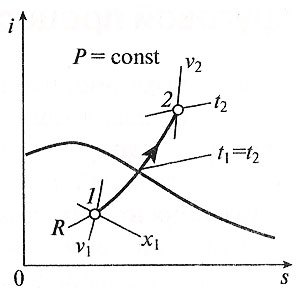
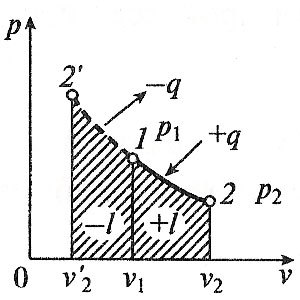
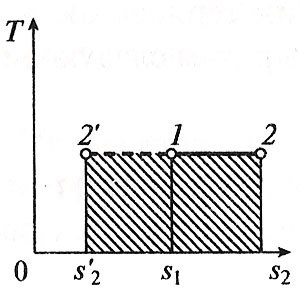
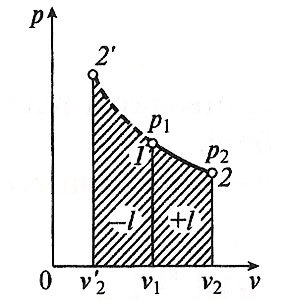
На фиг. 6.12 приведена схема теплофикационной установки, где показано, что охлаждающая вода, нагретая в конденсаторе К, не сбрасывается, а поступает в отопительные приборы потребителя. Температура воды для отопления должна быть не ниже 70—100 °С. Температура пара в конденсаторе (подогревателе) должна быть хотя бы на 10—15 0С выше. В большинстве случаев она получается больше 100 0С, а давление насыщенного пара p2 при этой температуре выше атмосферного. Поэтому турбины, работающие по такой схеме, называются турбинами с противодавлением. Итак, давление за турбиной с противодавлением получается обычно не менее 0,1—0,15 МПа вместо около 0,004 за конденсационной турбиной, что, конечно, приводит к уменьшению работы пара в турбине и соответствующему увеличению количества отбросной теплоты. Это видно на рис. 6.13, где полезно использованная теплота qц в конденсационном цикле изображается площадью 1-2'-3'-4'-5-6-1, а при противодавлении — площадью 1-2-3-4-5-6-1. Площадь 2-2'-3'-4 дает уменьшение полезной работы из-за повышения давления за турбиной с р'2 до р2. Повышение противодавления (конечного давления пара) приводит к уменьшению выработки механической или электрической энергии, но общее использование тепла при этом значительно повышается. Для идеального случая, в котором не учитываются неизбежные потери, коэффициент использования тепла в комбинированном процессе равен единице. В действительных условиях часть тепла теряется, и экономичность теплофикационных установок достигает 70—75%. Недостатком приведенной схемы является то, что отбор пара жёстко связан с его расходом через турбину. На практике потребности в электроэнергии и теплоте во времени не совпадают. Чтобы избавиться от такой жесткой связи, на станциях широко применяют турбины с регулируемым промежуточным отбором пара (рис. 6.14). Такая турбина состоит из двух частей: части высокого давления (ЧВД), в которой пар расширяется до давления pотб, необходимого для теплового потребителя, и части низкого давления (ЧНД), где пар расширяется до давления р2 в конденсаторе. Через ЧВД проходит весь пар, вырабатываемый котлоагрегатом. Часть его (при давление ротб) отбирается и посту-
пает к тепловому потребителю ТП. Остальной пар проходит через ЧНД в конденсатор К. Регулируя соотношения пара, проходящего через ЧНД и ТП, можно независимо менять как тепловую, так и электрическую нагрузки турбины с промежуточным отбором, чем и объясняется их широкое распространение на ТЭЦ. При необходимости предусматриваются два и более регулируемых отбора с разными параметрами пара. Наряду с регулируемыми каждая турбина имеет еще несколько нерегулируемых отборов пара, используемых для регенеративного подогрева питательной воды, существенно повышающего термический КПД цикла. Своеобразная «теплофикация» может осуществляться даже на чисто конденсационных станциях, где охлаждающая вода из конденсаторов используется, например, для обогрева бассейнов или водоемов, где искусственно выращивается рыба. Отбросная теплота может использоваться для обогрева парников, теплиц и т. д. Конечно, потребное в районе ТЭЦ количество теплоты для этих целей значительно меньше общего количества отбросной теплоты, но тем не менее такое ее использование является элементом безотходной технологии — технологии будущего. Загрузка... Несмотря на большие потери при передаче теплоты от продуктов сгорания в паровом котле к пару, КПД паросиловых установок в среднем выше, чем у ГТУ, и близок к КПД ДВС Большой располагаемый теплоперепад в турбине и связанный с этим относительно низкий удельный расход пара на выработку 1 кВт позволяют создать паровые турбины на колоссальные мощности — до 1200 МВт в одном агрегате. Поэтому паросиловые установки безраздельно господствуют как на тепловых, так и на атомных электростанциях. Паровые турбины применяют также для привода турбовоздуходувок (в частности, в доменном производстве). Недостаток паротурбинных установок — большие затраты металла, связанные прежде всего с большой массой котлоагрегата. Поэтому они практически не применяются на транспорте и их не делают маломощными. Классификации вентиляторов Вентиляторы классифицируются по многим параметрам, таким как: а) конструкция и принцип действия: могут быть осевыми, радиальными и диаметральными б) в зависимости от величины полного давления: могут быть низкого (до 1 кПа), среднего (до 3 кПа) и высокого давления (до 12 кПа) в) в зависимости от направления вращения рабочего колеса: могут быть правого и левого вращения г) в зависимости от состава перемещаемой среды: обычные, термостойкие, взрывобезопасные, пылевые и т.д. д) по месту установки: обычные, устанавливаемые на специальной опоре (раме,фундамент и т.д.); канальные, устанавливаемые непосредственно в воздуховоде; крышные, размещаемые на кровле. Основными характеристиками вентиляторов являются следующие параметры: · расход воздуха, м3/ч; · полное давление. Па; · частота вращения, об/мин; · потребляемая мощность, затрачиваемая на привод вентилятора, кВт; · КПД - коэффициент полезного действия вентилятора, учитывающий, механические потери мощности на различные виды трения в рабочих органах вентилятора., объемные потери. результате утечек через уплотнение и аэродинамические потери в проточной части вентилятора; · уровень звукового давления, дБ. КУиП 1 Основные аспекты экономичность работы котельного агрегата и определения коэффициента полезного действия. Коэффициент полезного действия и потери теплоты Коэффициент полезного действия, %, проектируемого парового котла определяется методом обратного баланса:
Задача расчета сводится к определению тепловых потерь для принятого типа парового котла и сжигаемого топлива. Потеря теплоты с уходящими газами
где
Здесь при паропроизводительности котла
при При нагрузках, отличающихся от номинальной, потери теплоты
Потери теплоты от наружного охлаждения системы пылеприготовления невелики; они в значительной мере компенсируются выделением теплоты при работе мельниц, и поэтому оба указанных фактора не учитываются. Разбивка потери тепла от наружного охлаждения котла по отдельным газоходам практически не сказывается на результатах расчета. Доли этой потери, приходящиеся на отдельные газоходы, для упрощения принимаются пропорциональными количеству тепла, отдаваемого газами в соответствующих газоходах. Поэтому при определении количества тепла, отданного газами, потери от наружного охлаждения учитываются введением коэффициента сохранения тепла
Потеря теплоты с физическим теплом шлака
где
Определение расхода топлива Полный расход топлива B, кг/с, подаваемого в топочную камеру парового котла, определяется из баланса между полезным тепловыделением при
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.209.122 (0.019 с.) |





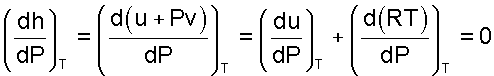









 :
: 



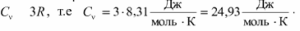





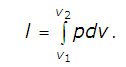
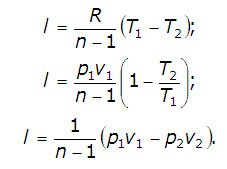
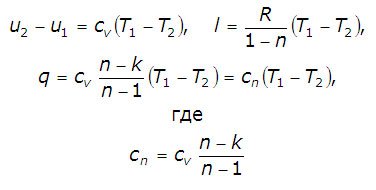




 . (4.21)
. (4.21) , %, зависит от заданной (выбранной) температуры уходящих газов и избытка воздуха продуктов сгорания покидающих котел
, %, зависит от заданной (выбранной) температуры уходящих газов и избытка воздуха продуктов сгорания покидающих котел . (4.22)
. (4.22) – энтальпия уходящих газов, кДж/кг или кДж/м3;
– энтальпия уходящих газов, кДж/кг или кДж/м3;  – энтальпия холодного воздуха;
– энтальпия холодного воздуха;  – располагаемая теплота сжигаемого топлива, кДж/кг или кДж/м3. В большинстве случаев
– располагаемая теплота сжигаемого топлива, кДж/кг или кДж/м3. В большинстве случаев  и только при внешнем (калориферном) подогреве воздуха перед поступлением его в воздухоподогреватель, а также при предварительном нагреве топлива (мазута) располагаемую теплоту определяют
и только при внешнем (калориферном) подогреве воздуха перед поступлением его в воздухоподогреватель, а также при предварительном нагреве топлива (мазута) располагаемую теплоту определяют  , где
, где  – коэффициент, учитывающий долю дополнительного поступления теплоты с топливом:
– коэффициент, учитывающий долю дополнительного поступления теплоты с топливом: . (4.23)
. (4.23) – температура мазута, обычно составляет 90–140 °С;
– температура мазута, обычно составляет 90–140 °С;  – нагрев воздуха в калориферной установке, °С (подогрев за счет рециркуляции горячего воздуха не учитывается). Потери теплоты с химическим
– нагрев воздуха в калориферной установке, °С (подогрев за счет рециркуляции горячего воздуха не учитывается). Потери теплоты с химическим 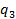 , %, и механическим
, %, и механическим  , %, недожогом топлива зависят от вида топлива и способа его сжигания. Потеря теплоты от наружного охлаждения
, %, недожогом топлива зависят от вида топлива и способа его сжигания. Потеря теплоты от наружного охлаждения  , %, через внешние поверхности в котлах большой тепловой мощности невелики (менее 0,5 %) и уменьшается с ростом единичной мощности котла. Ее значение при номинальной расчетной нагрузке можно определить из следующих зависимостей:
, %, через внешние поверхности в котлах большой тепловой мощности невелики (менее 0,5 %) и уменьшается с ростом единичной мощности котла. Ее значение при номинальной расчетной нагрузке можно определить из следующих зависимостей: = 42–250 кг/с (160–900 т/ч)
= 42–250 кг/с (160–900 т/ч) . (4.24)
. (4.24) . (4.25)
. (4.25) , (4.26)
, (4.26)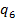 , %, обязательно учитывается при жидком шлакоудалении (при любой зольности топлива), а при твердом шлакоудалении – только в случае для многозольных топлив, когда
, %, обязательно учитывается при жидком шлакоудалении (при любой зольности топлива), а при твердом шлакоудалении – только в случае для многозольных топлив, когда  > 2,5
> 2,5  , (4.27)
, (4.27) = 1-
= 1-  – доля шлакоулавливания в топочной камере;
– доля шлакоулавливания в топочной камере;  – энтальпия шлака.
– энтальпия шлака.


